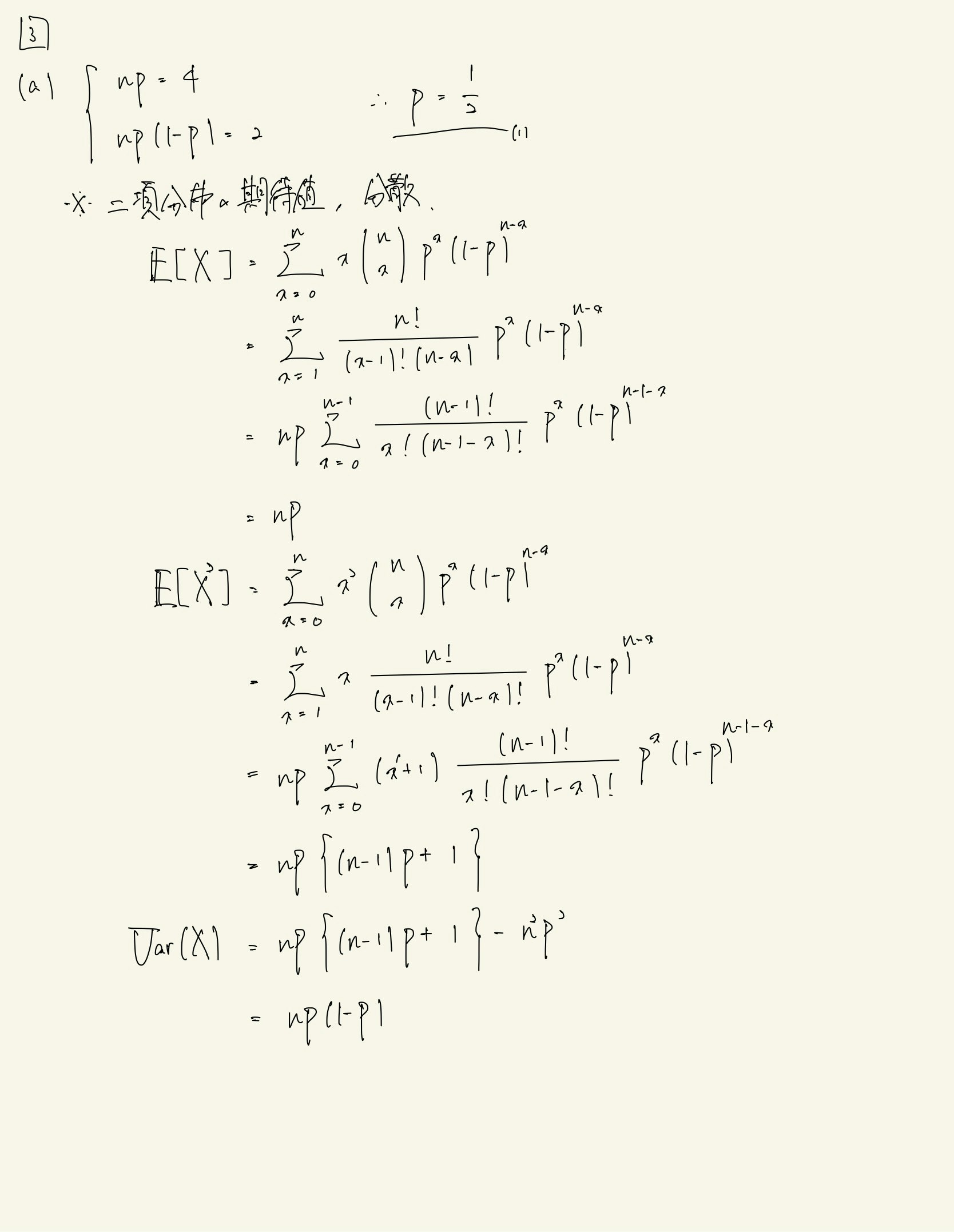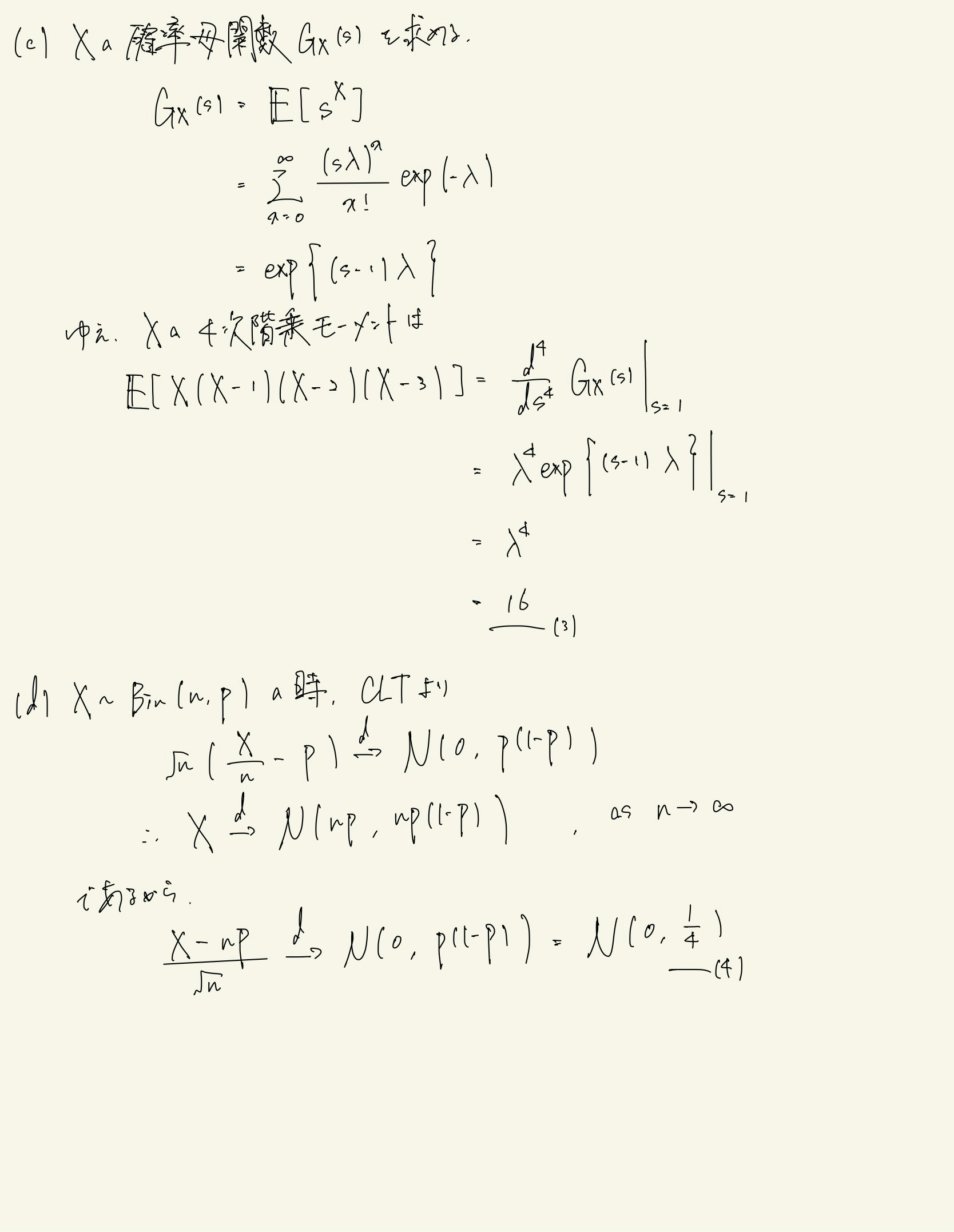方針
- (a) 二項分布の期待値,分散から連立方程式を解く.類題ではないが,二項分布は3.8で扱った.
- (b) 負の二項分布の期待値,分散から連立方程式を解く.期待値,分散を覚えていないと時間がかかってしまうので覚えていなければ飛ばすべき問題.負の二項分布は3.7で扱った.
- (c) ポアソン分布の四次階乗モーメントを確率母関数を使って求める.確率母関数は2.11で扱った.
- (d) 中心極限定理 (CLT) を使って二項分布に従う確率変数が収束する分布を求める.X/nとは,Ber(p)に従う確率変数の標本平均であるからCLTを適用できる.3.8では,CLTを使わずに二項分布の漸近正規性を導出した.
- (e) 指数分布に従う確率変数XのシーリングをYとすると,Yは幾何分布に従うことを使う.幾何分布の形が見えなくても期待値が導出できるよう補足を書いた.類題は3.6.
答案
参考文献
- 『現代数理統計学の基礎』(久保川達也 著)