はじめに
LoomはClojureのグラフ・ネットワークライブラリです。Loomは純Clojureで実装されており、基本的なネットワーク分析に必要な機能がそろっています。Clojureには統計解析等に関する優秀なツールがあり、データ分析には事欠きませんが、これでネットワーク分析も行うことができるようになります。
本稿では、Loomの基本的な使い方の説明と、実世界のネットワークを対象とした簡単な分析を行っていきます。
基本的な使い方
インストール
以下をLeiningenやBootの依存設定に追加します。
[aysylu/loom "0.6.0"]
グラフの生成・変更
グラフの作成や変更はloom.graphで行います。グラフを作成するには、
(require '[loom.graph :as lg])
(def g (lg/graph [1 2] [2 3] {3 [4] 5 [6 7]} 7 8 9))
とします。
ベクタ[1 2]からはノード1, 2、エッジ1-2が入り、マップ{3 [4] 5 [6 7]}からはノード3, 4, 5, 6, 7、エッジ3-4, 5-6, 5-7が入ります。ノード8, 9は他ノードとはつながっていません。
このグラフgは無向グラフです。有向グラフを生成するにはdigraphを使います。
(def dg (lg/digraph [1 2] [2 3] {3 [4] 5 [6 7]} 7 8 9))
エッジに重みを設定することもできます。ベクタの3番目の要素に数値を入れて、
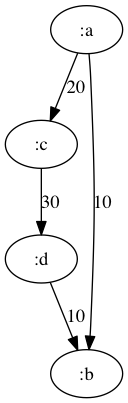
(def wdg (lg/weighted-digraph [:a :b 10] [:a :c 20] [:c :d 30] [:d :b 10]))
とします。
グラフのノードやエッジを取得するには、nodes, edgesを使います。
(lg/nodes g)
;;=> #{1 2 3 4 5 6 7 8 9}
(lg/edges wdg)
;;=> ([:c :d] [:d :b] [:a :b] [:a :c])
out-degree, in-degreeで、あるノードから外に出ていくエッジ、入ってくるエッジの数を求められます。
(lg/out-degree dg 5)
;;=> 2
(lg/in-degree dg 3)
;;=> 1
グラフにノードやエッジを追加したり、削除することもできます。
(lg/add-nodes g 10 11 12)
(lg/add-edges g [8 9] [10 11])
(lg/remove-nodes g 1 2 3)
(lg/remove-edges g [1 2] [2 3])
Loomのデータ構造はイミュータブルなため、これらの操作は元のグラフを変更しません。clojure.coreのコレクション操作関数と同様に、新しいグラフが返されます。実装をみると、グラフデータはレコードで作られていることがわかります。
(defrecord BasicEditableGraph [nodeset adj])
(defrecord BasicEditableDigraph [nodeset adj in])
(defrecord BasicEditableWeightedGraph [nodeset adj])
(defrecord BasicEditableWeightedDigraph [nodeset adj in])
グラフの可視化
LoomはGraphVizを利用してグラフを可視化します。システムにGraphVizをインストールしてから、
(require '[loom.io :as lio])
(lio/view wdg)
とすると、グラフをPNG画像に出力してくれます。
:algオプションにレイアウトアルゴリズムを指定することができます。たとえば:fdpを指定すると、ばねモデルを使ってレイアウトします。
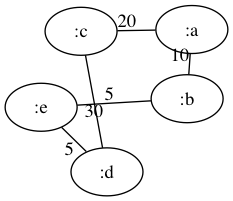
(def wg (lg/weighted-graph {:a {:b 10 :c 20} :c {:d 30} :e {:b 5 :d 5}})
(lio/view wg :alg :fdp)
経路探索
loom.algには経路探索などのアルゴリズムが実装されています。
以下はダイクストラ法を用いてノード:aからノード:dへの最短経路を求めます。
(require '[loom.alg :as la])
(la/dijkstra-path wg :a :d)
;;=> (:a :b :e :d)
経路長も知りたければ、dijkstra-path-distを使います。
(la/dijkstra-path-dist wg :a :d)
;;=> [(:a :b :e :d) 20]
:aから:dへの経路としては他に(:a :c :d)が考えられますが、その場合の経路長は25なので、ちゃんと最短経路が返ってきていることがわかります。
loom.algには経路探索以外のアルゴリズムもあるので、興味がある方はドキュメントやソースコードを読んでみるとよいと思います。
実践
次に、実世界のデータを使って簡単なネットワーク分析をしてみます。
データセット
今回はSNAPのWebサイトにあるデータを使います。
https://snap.stanford.edu/data/egonets-Twitter.html
上記ページにある、
- twitter.tar.gz
- twitter_combined.txt.gz
をダウンロードして解凍しておきます。
前者には多くのファイルが含まれます。.edgesという拡張子のファイルには、1行ごとにスペースで区切られた2つのノードが書かれています。1行が1つのエッジをあらわしています。
163629705 32122637
31477674 163629705
88491375 28719244
...
ひとつのファイルに、ひとつのエゴネットワークの情報が入っています。エゴネットワークとは、ある起点ユーザとリンクするユーザを集めたネットワークです。ただし、この.edgesファイルには起点ユーザは含まれていません。
使用ライブラリ
Loomの他に、チャートを描画するためにIncanter、組み合わせを求めるためにmath.combinatoricsを依存に加えておきます。
[aysylu/loom "0.6.0"]
[incanter "1.5.7"]
[org.clojure/math.combinatorics "0.1.3"]
準備
以降のコードは全てREPL上で入力することを想定して記述します。
まずは、ファイルからエッジ情報を読み込み、ベクタのシーケンスを返す関数を作るところからはじめます。
(require '[clojure.java.io :as io]
'[clojure.string :as string])
(defn load-edges
[file]
(with-open [rdr (io/reader file)]
(->> (line-seq rdr)
(map #(string/split % #" "))
(doall))))
この関数を使ってグラフを作成してみます。小さめのファイルを使って動作確認しましょう。
(require '[loom.graph :as lg]
'[loom.io :as lio])
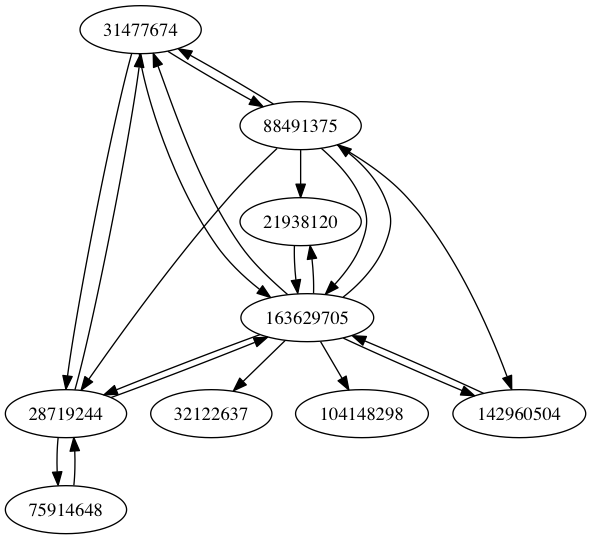
(def small-g (apply lg/digraph (load-edges "path/to/twitter/396721965.edges")))
(count (lg/nodes small-g))
;;=> 9
(count (lg/edges small-g))
;;=> 26
(lio/view small-g)
ノード数9、エッジ数26のネットワークのようです。有向グラフとして作成したので、可視化すると以下のように矢印がつきます。2ノード間で互いに矢印があるのは、Twitterにおける相互フォローですね。
今度は大きめのデータを使ってみます。データセットに含まれる各エゴネットワークのエッジ全てを連結したtwitter_combined.txtをロードします。今回は簡略化のため無向グラフにします。それなりに時間がかかります。
(def large-g (apply lg/weighted-graph (load-edges "path/to/twitter_combined.txt")))
(count (lg/nodes large-g))
;;=> 81306
(count (lg/edges large-g))
;;=> 2684606
ノード数が81,306、エッジ数が2,684,606という大きなネットワークです。ネットワークが大きいのでviewで可視化するのはやめておきしょう。
このネットワークに対して、実世界のネットワークによくあらわれるスケールフリー性、スモールワールド性、クラスタ性がみられるかを調べてみます。ただし、今回のデータセットはエゴネットワークを連結したものなので、Twitter全体のネットワークの性質を示せるわけではないことに注意してください。
スケールフリー性
out-degreeを使うと、あるノードに接続するエッジの数を求めることができました。Twitterの場合は、あるユーザのフォローしているあるいはフォローされている数ということになります。Clojureの統計解析ツールIncanterと組み合わせて、分布を可視化してみましょう。
(require '[incanter.core :as i]
'[incanter.charts :as ic])
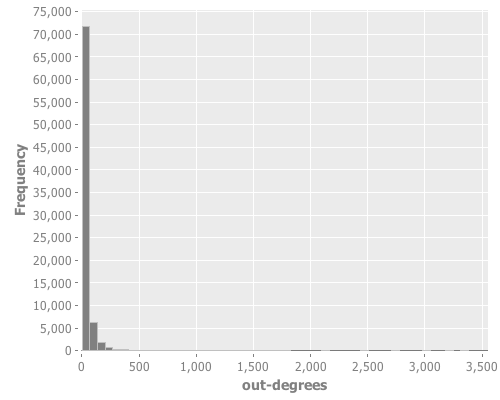
(let [out-degrees (map #(lg/out-degree large-g %) (lg/nodes large-g))]
(i/view (ic/histogram out-degrees :nbins 50)))
Twitterでは、大多数のユーザのフォロワーは少ないですが、一方でごく一部のユーザが多くのフォロワーを抱えています。このようにノードの次数がべき乗分布に従うことをスケールフリー性といいます。
スモールワールド性
次に、ネットワークの平均経路長、すなわちあるユーザからあるユーザまで平均で何人たどればたどりつけるかを調べてみます。全ての組み合わせの経路長を計算するのは骨が折れるので、ここではランダムに1,000件のノード組み合わせを取り出して、その経路長を計算することにします。経路長計算は重い処理なのでpmapで並列化して走らせましょう。
(require '[loom.alg :as la])
(def dists (let [nodes (vec (lg/nodes large-g))]
(->> (repeatedly #(vector (rand-nth nodes) (rand-nth nodes)))
(remove #(= (first %) (second %)))
(distinct)
(take 1000)
(pmap (fn [[n1 n2]]
(la/dijkstra-path-dist large-g n1 n2)))
(map second))))
平均をとります。
(double (/ (reduce + dists) (count dists)))
;;=> 3.906
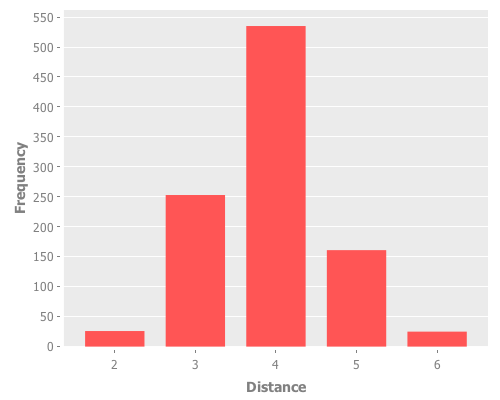
このネットワークの平均経路長は3.906のようです。だいたい3ユーザを間にはさめば、どのユーザにも到達できるということになります。このような「世間は広いようで狭い」現象をスモールワールド性といいます。
分布は以下のような感じです。
(let [freqs (sort-by first (frequencies dists))]
(i/view (ic/bar-chart (map first freqs)
(map second freqs)
:x-label "Distance"
:y-label "Frequency")))
3.906は割と小さい値なのですが、Twitterの全ネットワークよりもかなり小さく、制約のあるデータセットなので、こんなものでしょう。ちなみにFacebookの平均経路長は4.571、mixiは5.42のようです。
クラスタ性
クラスタ性とは「友達の友達は友達」というような性質です。これはネットワークの平均クラスタ係数によって調べることができます。まず、あるノードのクラスタ係数を求める関数を作ります。
(require '[clojure.math.combinatorics :as combo])
(defn clustering-coefficient
[g node]
(let [successors (lg/successors g node)
nsuccessors (count successors)]
(if (> nsuccessors 1)
(/ (count (filter (fn [[n1 n2]]
(lg/has-edge? g n1 n2))
(combo/combinations successors 2)))
(/ (* nsuccessors (dec nsuccessors)) 2))
0)))
クラスタ係数は、隣接ノードのうちエッジが結ばれている組み合わせがどのくらいあるかの割合です。successorsで隣接ノードを取得し、その全ての組み合わせをmath.combinatoricsのcombinationsで求め、エッジが存在するかをhas-edge?を使って計算しています。
この関数を用いて、ネットワークの全ノードについてクラスタ係数を求め、平均値を求めます。
(let [coeffs (map #(clustering-coefficient large-g %) (lg/nodes large-g))]
(double (/ (reduce + coeffs) (count coeffs)))
;;=> 0.5653293415705775
実世界のネットワークの平均クラスタ係数は0.1〜0.75程度3といわれているので、クラスタ性を示しているといえそうです。
おわりに
Clojureでネットワーク解析などをしたいときに使えるライブラリとしてLoomを紹介しました。Loomは純Clojureで実装されており、そのデータ構造はイミュータブルなため、Clojureで解析を行うときには相性が良さそうです。基本的なネットワーク分析には十分使えると思います。
一方で、Loomにはページランクなどの中心性の計算のような高度なアルゴリズムが実装されていません。また、グラフの可視化に外部ツールであるGraphVizが必要となります。そこで私は、より高度な解析が必要なときのために、Jungererというライブラリを開発しています。基本的な使い方を以下の記事で紹介しています。
グラフやネットワークを扱うClojureライブラリ「Jungerer」 - totakke blog