【Unity】【音】AMDFで音声波形からリアルタイルに音階を判定する

波形に含まれる周波数成分を取り出そうとする時、フーリエ変換せずとも周波数成分を割り出すことができます。
AMDFという、自己相関によって波形データから周波数成分を求める方法があります
https://pdfs.semanticscholar.org/7e00/c103c0197a05f9d20511ef03fd8bb0ba81a5.pdf
ので、これを試してみます。

実行環境：Unity5.6.0f3

AMDFとは

AMDFとは Average Magnitude Difference Function の略だそうで、
要するに、

「100Hzの周波数の波形データ」と、

それを1/50秒ずらしたものとを比較すると

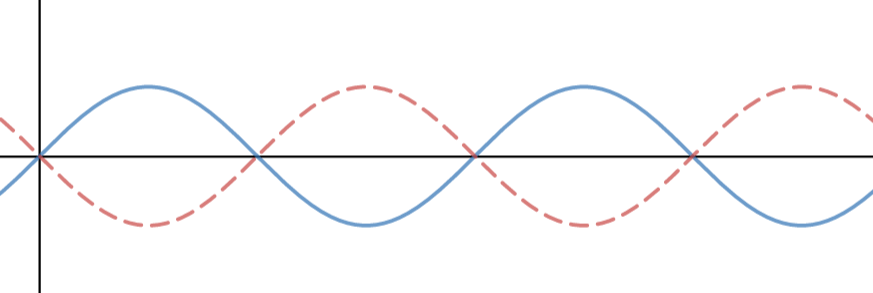
当然、全然一致しません。

が、1/100秒ずらしたものとを比較すると

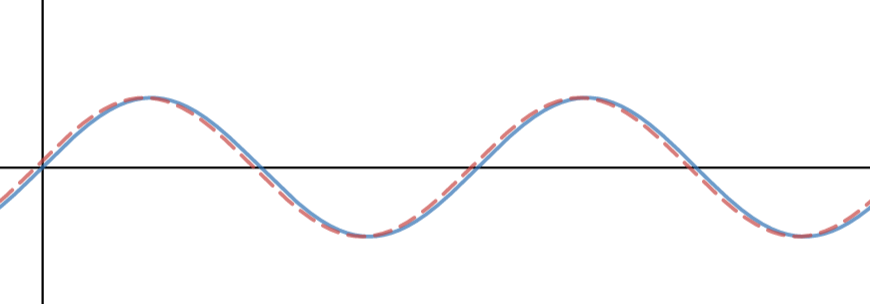
完全に一致します。

これを応用して、少しずつずらす量を変えて自己相関関数をかけまくり、「ずらした量と一致率」の関係から、波形データに含まれる周波数成分を取り出す、という考え方です。

※グラフの生成には https://www.desmos.com/calculator を利用させて頂いています。ありがとうございます。

ずらす量を少しずつ変えて自己相関関数をかけまくり

実装にあたって以下の資料を参考にしました。
https://www.utdallas.edu/~hynek/citing_papers/Mamun_A%20High%20Resolution%20Pitch%20Detection%20Algorithm.pdf

Unityでは、AudioSourceのclipに任意の音声データを割り当てておけば簡単に波形データを取得することができます。
波形データはAudioSource.GetOutputDataから取得することができます。
https://docs.unity3d.com/jp/current/ScriptReference/AudioSource.GetOutputData.html

void Start()
{
    audioSource = GetComponent<AudioSource>();
}
void Update()
{
    audioSource.GetOutputData(outputData, 0);
}

※マイクから拾う場合はこのように初期化すればOK

    var audioSource = this.GetComponent<AudioSource>();
    audioSource.loop = true;
    audioSource.clip = Microphone.Start(deviceName, true, 10, 44100);
    while (!(Microphone.GetPosition(deviceName) > 0)) { }
    audioSource.Play();

仮に440Hzの場合を考えます。

AudioSettings.outputSampleRateが48000だとすると、
440Hzは１周期が440分の一秒ですから、48000 / 440 ≒「109」だけ、インデックスをずらした波形データで比較していくことになります。
つまり、OutputData[0]とOutputData[109]、OutputData[1]とOutputData[110]、OutputData[2]とOutputData[111]・・・とせっせと比較していけば良いことになります。

    // 誤差の総和を求めて、
    int offset = (AudioSettings.outputSampleRate / 440);
    int N = outputData.Length - offset;
    for (int n = 0; n < N; ++n) {
        diff += Mathf.Abs(outputData[n] - outputData[n + offset]);
    }
    // 比較した回数で割る
    diff *= 1f / N;

なお、AudioSettings.outputSampleRateが48000だった場合、GetOutputDataの参照するインデックスを１ずらすごとに1/48000秒、時間がずれることになり、これが分解能になります。このため、
440Hzの１周期にかかる時間は約109.09/48000秒、
439Hzの１周期にかかる時間は約109.34/48000秒、
となり、ずらすべき量が同じため、440Hzと439Hzは単純には比較できないことになります。

含まれる周波数成分を求める

まずはこのように、0~200の範囲でインデックスをずらし、ずらした量ごとの誤差を割り出すようにします。

    float[] diff = new float[max - min + 1];
    for (int m = 0; m <= 200; ++m) {
        int N = outputData.Length - m;
        for (int n = 0; n < N; ++n) {
        diff[m - min] += Mathf.Abs(outputData[n] - outputData[n + m]);
        }
        diff[m - min] *= 1f / N;
    }

ラ（A4）を聞かせ、diffの中身を可視化してみますと、

このようになります。
誤差が小さいほど「谷」になることになります。
中央やや右、「109」ずらしたところに谷（誤差が小さい）があるのが分かります。

※ちなみに、ラ（A4）の周波数スペクトラムは以下のような形になり、440Hz以降、880Hz、1320Hz・・・と倍振動によるスパイクが見られます。

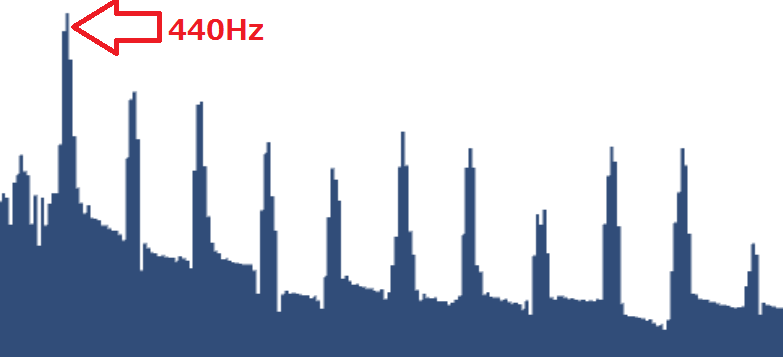
これを応用して音階を推定する

実装の概略を示します。

    List<float> keyHzList = new List<float> {
        27.500f,	// 最低音（A0）
        29.135f,
        ・・・
        440.000f,       // ラ（A4）
        ・・・
        4186.009f,	// 最高音（C8）
    };
    audioSource.GetOutputData(outputData, 0);
    float[] keys = new float[88];
    for(int key = 0; key < 88; ++key) {
        float hz = keyHzList[key];
        int m = (int)(AudioSettings.outputSampleRate / hz);
        int N = outputData.Length - m;
        float diff = 0f;
        for (int n = 0; n < N; ++n) {
            diff += Mathf.Abs(outputData[n] - outputData[n + m]);
        }
        diff *= 1f / N;
        keys[key] = diff;
    }

これで求めた「88鍵分の誤差」から、近しいところと比較して「誤差が相対的に小さい鍵盤が弾かれている」と判断し、鍵盤にマッピングしてみますと、

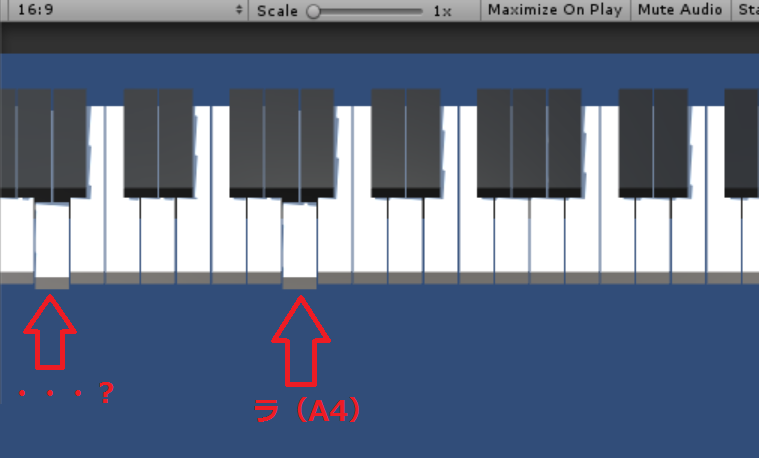
ラ（A4）を検出できています。

と同時に、その１オクターブ下のラ（A3）も検出しています。
ラ（A4）、つまり440Hzについて調べようとする時、インデックスを「109」ずらして比較しているのでした。
「109」ずらした時に一致率の高い波形データは、当然ながら、その整数倍「218」「327」ずらした時も一致率が高いことになります。
そして、１オクターブ下のラ（A3）、220Hzについて調べようとする時、220Hz/48000≒「218」となり、ここでは両者の区別が付かなくなっていることによります。

低い計算量で一定の精度を得られる

リアルタイムな応答を求められ、かつ計算資源の限られた環境では、有効な手段の一つと言えそうです。