Exercise 3.2: Turing numbers
Suppose one Turing machine contains following program lines:
\begin{aligned}
&1: \, \langle q_0,\Gamma_0,q_0,\Gamma_0,+1 \rangle \\ &2: \, \langle q_0,\Gamma_1,q_1,\Gamma_1,0 \rangle
\end{aligned}
where $q_0 = q_s, q_1 = q_H$.
We encode each program line $\langle q,x,q',x',s \rangle$ as follows:
- The state $q_\rm{i}$ is encoded by the letter 'D' followed by the letter 'A' repeated i times
- The alphabet of symbol $\Gamma_{\rm i}$ is encoded by the letter 'D' followed by the letter 'C' repeated i times
- The movements of tape-head (-1, +1, and 0) are encoded by the letter 'L', 'R', and 'N', respectively.
Therefore, a program line $\langle q_0,\Gamma_0, q_0, \Gamma_0, +1)$ is encoded as $${\rm DDDDR}.$$
By separating program lines by semicolons we then can describe the program as $${\rm DDDDR;DDCDADCN}.$$
Then we replace each of the symbols as follows:
\begin{aligned}
{\rm 'D'} &\to 0 \\
{\rm 'A'} &\to 1 \\
{\rm 'C'} &\to 2 \\
{\rm 'L'} &\to 3 \\
{\rm 'R'} &\to 4 \\
{\rm 'N'} &\to 5 \\
{\rm ';'} &\to 6.
\end{aligned}
The result is 0-0-0-0-4-6-0-0-2-0-1-0-2-5.
Since every positive integer has a unique prime factorization $p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}$, where $p_i$ are distinct prime numbers, and $a_1, \cdots, a_k$ are non-negative integers, we can use this product as a Turing number for this program. Thus the number is
\begin{aligned}
2^0 \times 3^0 \times 5^0 \times 7^0 \times 11^4 \times 13^6 \times 17^0 \times 19^0 \times 23^2 \times 29^0 \times 31^1 \times 37^0 \times 41^2 \times 43^5.
\end{aligned}
Exercise 3.3: Turing machine to reverse a bit string
Suppose we have a two-tape Turing machine which takes as input a binary numbers on the first tape and blanks on the remainder of both tapes, except the endpoint marker $\rhd$. The machine contains following program lines can outputs the bits of $x$ in reverse order on the second tape.
\begin{aligned}
1&: \, \langle q_s, \rhd, \rhd, q_1, \rhd, \rhd, +1, +1 \rangle \\
2&: \, \langle q_1, 0, b, q_1, 0, b, +1, 0 \rangle \\
3&: \, \langle q_1, 1, b, q_1, 1, b, +1, 0 \rangle \\
4&: \, \langle q_1, b, b, q_2, b, b, -1, 0 \rangle \\
5&: \, \langle q_2, 0, b, q_2, b, 0, -1, +1 \rangle \\
6&: \, \langle q_2, 1, b, q_2, b, 1, -1, +1 \rangle \\
7&: \, \langle q_2, \rhd, b, q_H, \rhd, b, 0, 0 \rangle
\end{aligned}
Exercise 3.4: Turing machine to add modulo 2
Suppose we have a two-tape Turing machine which takes as input a binary numbers on the first tape. The machine contains following program lines can outputs the bits of $x$ in reverse order on the second tape.
\begin{aligned}
1&: \, \langle q_s, \rhd, \rhd, q_1, \rhd, \rhd, +1, +1 \rangle \\
2&: \, \langle q_1, 0, b, q_2, 0, 0, +1, +1 \rangle \\
3&: \, \langle q_1, 1, b, q_2, 1, 1, +1, +1 \rangle \\
4&: \, \langle q_2, 0, b, q_2, 0, b, +1, 0 \rangle \\
5&: \, \langle q_2, 1, b, q_2, 1, b, +1, 0 \rangle \\
6&: \, \langle q_2, b, b, q_3, b, b, +1, -1 \rangle \\
7&: \, \langle q_3, 0, 0, q_H, 0, 0, 0, 0 \rangle \\
8&: \, \langle q_3, 1, 0, q_H, 1, 1, 0, 0 \rangle \\
9&: \, \langle q_3, 0, 1, q_H, 0, 1, 0, 0 \rangle \\
10&: \, \langle q_3, 1, 1, q_H, 1, 0, 0, 0 \rangle
\end{aligned}
Exercise 3.5: Halting problem with no inputs
Define A(x) as the program that outputs "YES" if arbitrary program $M$ halts, and outputs "NO" if it doesn't. That is,
A(M) = \begin{cases} \text{YES} &\,\,\, \text{if program $M$ halts,} \\ \text{NO} & \,\,\, \text{otherwise.} \end{cases}
Define B(M) as the program that never halts if $A(M)=\text{"YES"}$, and halts if $A(M)=\text{"NO"}$. It follows from the definition of $B(M)$ that exactly one of the following two cases must be hold:
- $A(M)=\text{"YES"}$ and so $B(M)$ never halts. In this case $B(B(M))$ halts.
- $A(M)=\text{"NO"}$ and so $B(M)$ halts. In this case $B(B(M))$ never halts.
In either cases there is a conflict. Therefore, there is no algorithm to determine whether $M$ halts with no inputs.
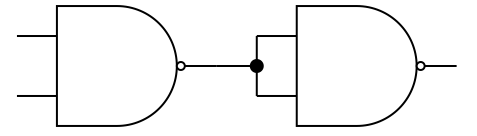
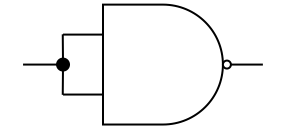
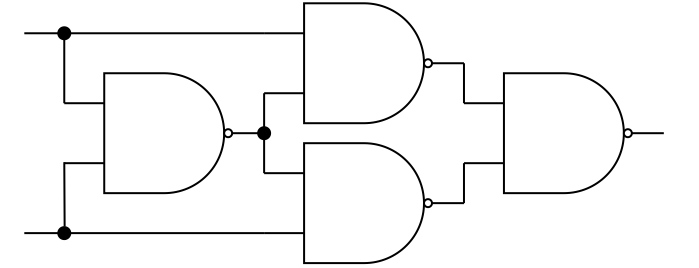
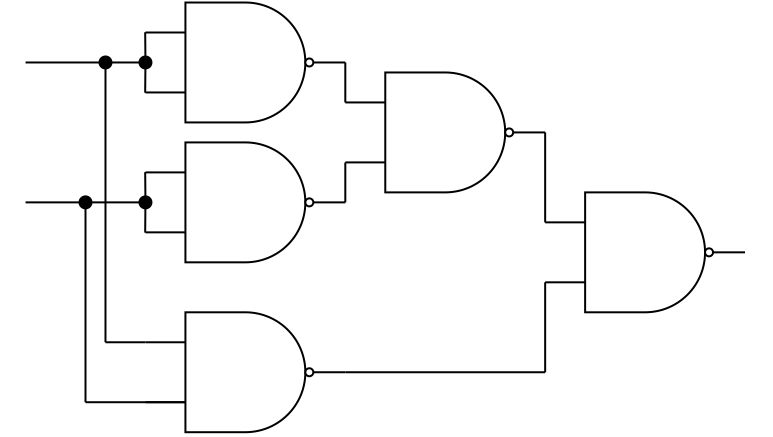
Exercise 3.8: Universality of NAND
Exercise 3.9
We say $f(n)$ is $\mathcal{O}(g(n))$ if there are constants $c$ and $n_0$ such that for all values of $n$ greater than $n_0$, $f(n) \leq cg(n)$, which means $\frac{1}{c}f(n) \leq g(n)$. Therefore, $f(n)$ is $\mathcal{O}(g(n))$ if and only if $g(n)$ is $\Omega(f(n))$.
We say $f(n)$ is $\Theta(g(n))$ if $f(n)$ is $\mathcal{O}(g(n))$ and $f(n))$ is $\Omega(g(n))$, which means $c_1g(n) \leq f(n)$ and $f(n) \leq c_2g(n)$. Therefore, $f(n)$ is $\Theta(g(n))$ if and only if $g(n)$ is $\Theta(f(n))$.
Exercise 3.10
Since $g(n)$ is a polynomial of degree $k$, it can be written as
g(n) = c_1n^k + \mathcal{O}(n^{k-1}).
Apparently, there exists a constant c which suffice $g(n) \leq cn^l$ for any $l \geq k$.