前回、言語を作る!(JavaCCの環境構築編)でJavaCCの開発環境を整えました。
今回は簡単な電卓を作成して、JavaCCの使い方を学んでみます。
JavaCCの仕組み
JJTファイルを作るとJavaCCはJavaのParserを生成してくれます。JJTファイルとは字句解析と構文解析を定義したファイルです。
インタープリタやコンパイラの処理の流れ
- 前処理 (ソースファイルを一括置換したり、省略された記述を補完など。)
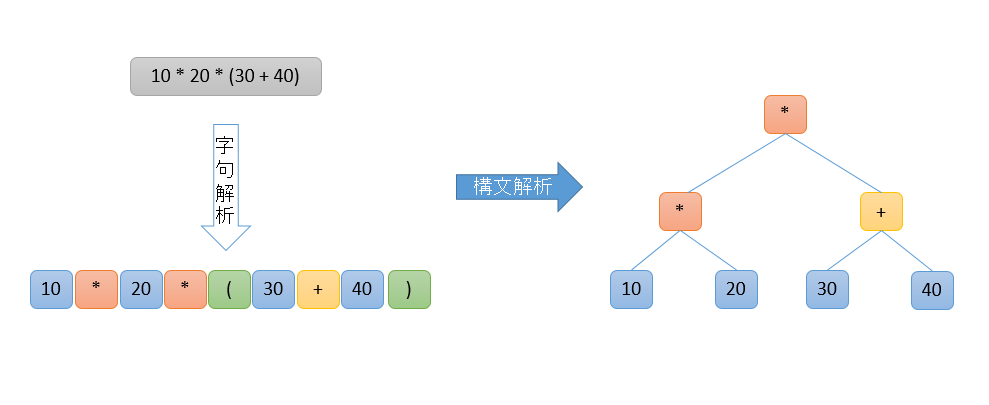
- 字句解析 (ソースコードを適切な字句に切り分け。)
- 構文解析 (字句をもとに構文木を生成。)
- 意味解析 (構文木の意味を解釈。インタープリタによってはそのまま実行。)
- 機械語やバイトコードの生成
- マシンやVMがコードを実行
今回は特に字句解析、構文解析、意味解析(構文木の実行)を中心に話を進めます。
言語の形式表現
ここではまずJavaCCを使う前に言語というものに関して前準備を行います。その言語がどういうものであるかを記述したり、適切に解析するための方法を考えます。
BNF
BNFとは、言語の文法を定義するための言語です。左辺を右辺で定義していく形式で記述されます。
BNFの記述方法は様々な流儀がありますが、今回はJavaCCに合わせて正規表現風のBNFの記述をします。
記述の簡便さは拡張されたBNF(extendes BNF)くらいになると思われます。
主に使われる記号は以下の通りです。
| 記号 | 意味 | 例 |
|---|---|---|
::= |
左辺を右辺で定義する | <式> ::= <加算式> |
() |
()内のグルーピング。 |
("+" | "-") |
<xxx> |
非終端記号。抽象的な式や文といったものは非終端となる。 | <式> |
"xxx" |
終端記号。具体的な文字や数字になると終端となる。 | "1" |
* |
直前を0回以上繰り返す | ("1" | "2")* |
+ |
直前を1回以上繰り返す | ("1" | "2")+ |
| | | またはを表す | "1" | "2" |
以降は下の単純な計算式について考えていくことにします。
<式> ::= <加算式>
<加算式> ::= <乗算式> ( <加算演算子> <乗算式> )*
<乗算式> ::= <単項式> ( <乗算演算子> <単項式> )*
<単項式> ::= <開括弧> <式> <閉括弧> | <10進数表現>
<加算演算子> ::= "+" | "-"
<乗算演算子> ::= "*" | "/" | "%"
<開括弧> ::= "("
<閉括弧> ::= ")"
<10進数表現> ::= (<数字>)+ ("." (<数字>)+)?
<数字> ::= "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" | "0"
このBNFについて確認してみましょう。
例えば、10 * 20 * (30 + 40)という計算式は
<式>
→ <加算式>
→ <乗算式> ( <加算演算子> <乗算式> )*
→ <乗算式>
→ <単項式> ( <乗算演算子> <単項式> )*
→ <単項式> <乗算演算子> <単項式> <乗算演算子> <単項式>
→ <10進数表現> <乗算演算子> <単項式> <乗算演算子> <単項式>
→ (<数字>)+ ("." (<数字>)+)? <乗算演算子> <単項式> <乗算演算子> <単項式>
→ <数字> <数字> <乗算演算子> <単項式> <乗算演算子> <単項式>
→ 10 <乗算演算子> <単項式> <乗算演算子> <単項式>
→ 10 * <単項式> <乗算演算子> <単項式>
→ ...
→ 10 * 20 * <単項式>
→ 10 * 20 * <開括弧> <式> <閉括弧>
→ 10 * 20 * ( <式> <閉括弧>
→ 10 * 20 * ( <加算式> <閉括弧>
→ 10 * 20 * ( <乗算式> ( <加算演算子> <乗算式> )* <閉括弧>
→ 10 * 20 * ( <乗算式> <加算演算子> <乗算式> <閉括弧>
→ ...
→ 10 * 20 * ( <単項式> <加算演算子> <乗算式> <閉括弧>
→ ...
→ 10 * 20 * ( 30 <加算演算子> <乗算式> <閉括弧>
→ ...
→ 10 * 20 * ( 30 + 40 )
のように導出できることが分かります。
字句解析
字句解析は文字の羅列を適切な区切りで区切る作業のことです。BNFではより終端記号に近い部分の解析を行うことになります。
<加算演算子> ::= "+" | "-"
<乗算演算子> ::= "*" | "/" | "%"
<開括弧> ::= "("
<閉括弧> ::= ")"
<10進数表現> ::= (<数字>)+ ("." (<数字>)+)?
<数字> ::= "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" | "0"
このとき、数字や10進表現、加算演算子は字句の種類という考え方をします。イメージとしては一連の文字列を適当に切り分ける作業です。
構文解析
BNFの中でも特に意味のある部分(構文木を作ることに意味がある部分)を構文解析で取り扱うことになります。
<式> ::= <加算式>
<加算式> ::= <乗算式> ( <加算演算子> <乗算式> )*
<乗算式> ::= <単項式> ( <乗算演算子> <単項式> )*
<単項式> ::= <開括弧> <式> <閉括弧> | <10進数表現>
字句解析で適当に切り分けた字句をノードとする木を組み立てていく作業になります。この木を組み立てる方法は上向き構文解析や下向き構文解析といったさまざまな手法があります。
今回のJavaCCは再帰降下型構文解析が用いられます。
字句解析と構文解析の役割
実は構文解析と字句解析の明確な線引きは難しいと言えます。例えば、単項式の頭に+や-をつけられるようなとき、
+10で一つの字句にしてしまうか、-と10の二つの字句として扱うかは作り方によります。
(ただし、この場合は+や-は中置演算子なのか、前置演算子なのかの判断は、文脈によるのでそれぞれ別の字句として扱い、構文解析の段階で判断させる方が扱いやすいかもしれません。)
次回
今回のBNFをJavaCCのjjtファイルに落とし込んでみます。
言語を作る!(シンプルな電卓を作る編②)に続きます。
関連記事
言語を作る!bisonとflexを使ってみた
言語を作る!(JavaCCの環境構築編)
言語を作る!(シンプルな電卓を作る編②)