交互作用について勉強する機会があったのでまとめてみた

初めに

線形回帰の勉強をしているときにこの**交互作用（Interaction）**という言葉に出会いました。なんだろうこれはと思いながら色々調べているうちになんとなく理解できたので、忘れないように記事にまとめようていきます。あくまで、個人的な理解なので間違っていたらご指摘ください。

交互作用とは

こちらのサイトによると、交互作用とは
「２つの因子が組み合わさることで初めて現れる相乗効果」
のことらしいです。なんとなくは分かる気がするのですが、ほんわかしている感じです。なので、今回は交互作用を重回帰分析を用いて説明していこうと思います。
ちなみに参考にしたサイトはこちらです。

• 回帰分析による交互作用の検証

重回帰分析は２つ以上の説明変数を用いて一つの目的変数を導き出すというものです。
　　　　　　　　　　

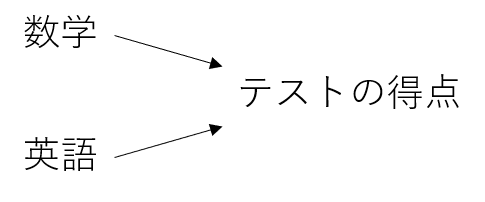
少し極端ですが、上の図のように「数学」と「英語」の得点から「テストの得点」の予測値を導く感じです。
具体的にはそれぞれの説明変数の係数を計算で求めていき、$y=ax+bz$のような式を導出します。一見すると数学と英語は独立変数であり、互いに関係がないように感じるかもしれません。
実際に、交互作用を考えずに導出した線形回帰の式は、一つの説明変数が他の説明変数によらず目的変数と一定の関係になっています。つまり、数学の得点が上がれば、英語の得点によらずテストの得点は上がるということです。
しかし、数学の得点が高いからといってそこに英語の得点が関わってこないのでしょうか。実はこの考えが交互作用なのですが、以下に例を挙げてみますと

• 数学の得点が高い人は、（数学の得点が一定の時に）英語の得点が高いほどテストの予想得点が高い
• 数学の得点が低い人は、（数学の得点が一定の時に）英語の得点が高いほどテストの予想得点が高い

というような可能性を考えるということです。このように、お互いの説明変数の相関関係のようなものを考えることが交互作用になると自分は理解しています。（間違っていたらご指摘お願いします）

ちなみに交互作用があるかどうかは、交互作用の項が回帰式において統計的に有意であるかどうかを調べることにより分かります。有意性についてはこちらのサイトを見てみてください。

• 有意性のお話

交互作用の項とは、関係性を調べたい説明変数同士の積の形になります。具体的に回帰式にどのように組み込まれるのかみていきます。

\begin{align}
テストの予想点&＝切片＋a×数学＋ｂ×英語＋ｃ×(数学×英語)\\
&＝(切片＋ｂ×英語)＋(a＋ｃ×英語)×数学
\end{align}

上の式を見てお気づきかもしれませんが、回帰式に数学と英語の積の項つまり交互作用の項が組み込まれています。なぜ積なのかというお話を少ししますと、こちらも式変形を見てお気づきかもしれませんが、第二項の数学の項の係数を見てみてください。
この数学の項が$a$という係数と$c×英語$にまとめることができるはずです。そして、$c$の値によって数学の得点と英語の得点の作用を確認することができるのです。
ここで先程紹介した統計的なt値やp値などを使い、有意差が5％以下であれば英語と数学の間には交互作用があるということになるのです。また、このように式変形して交互作用を考えることができるため、交互作用を確認したい説明変数の積を考えるのです。
ちなみにすごい回帰分析の検定についてわかりやすいサイトを見つけたので以下サイトを興味がある方は見てみてください。

• t検定とは？種類と手順を解説！

実験

それでは、試しにということで実践をしていきます。
今回使うデータはこちらの物件のデータを使って、お取り物件を検知するモデルを構築していきます。

• bukken_test.csv
• bukken_train.csv

まずは必要ライブラリの読み込みます。
jupyter notebookを使っているので%matplotlib inlineをつけときます。

.py

%matplotlib inline

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeClassifier 
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import cross_val_score

trainデータとtestデータを読み込みます。

.py

bukken_train = pd.read_csv("bukken_train.csv")
bukken_test = pd.read_csv("bukken_test.csv")

##データ前処理
データに何が含まれているのか気になるので確認します。

.py

bukken_train.head()
bukken_test.head()

確認したところ文字列のデータがあったのでダミー変数に置き換えます。

.py

#ダミー変数化をまとめてするためtrainとtestを統合
bukken = pd.concat([bukken_train,bukken_test])

#ダミー変数化対象
categoricals = ["use_classification", "land_shape", "frontal_road_direction", "frontal_road_kind"]

#ダミー変数作成
bukken_dummy = pd.get_dummies(bukken[categoricals],drop_first=True)

#新しくダミー変数に置き換える
bukken2 = pd.concat([bukken.drop(categoricals,axis=1),bukken_dummy],axis=1)

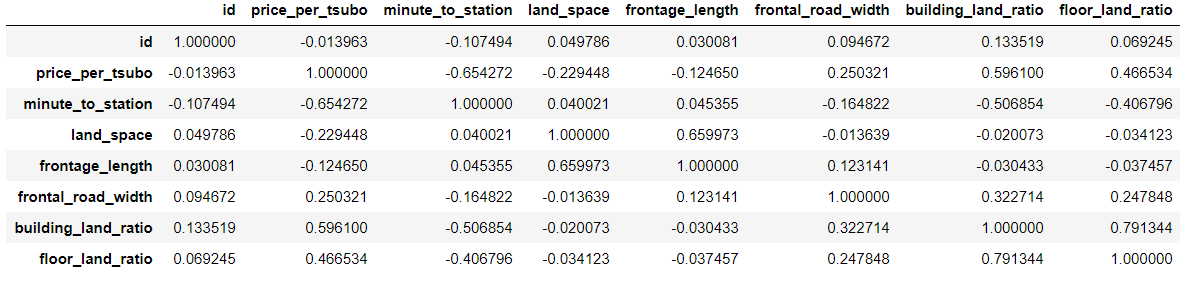
土地の値段と他の変数にどのような関係があるのか事前に確認したいので、相関行列を作成します。交互作用を考えるにあたり、全部の可能性を考慮するのが一番良いかもしれませんが、それはスマートではないなと感じたのでこのように相関を把握した上で交互作用を考えていきます。

.py

bukken_train2.corr().style.background_gradient(axis=None)

一部だけしか表示していませんが、土地代と駅からの時間が一番相関が高かったので、今回は駅からの時間とその他の変数の交互作用を考えてみることにします。

.py

#時間とland_shapeとの交互作用
m_neartyo,m_hu,m_tyo,m_nearsei,m_nearseikei,m_dai,m_sei,huku=[],[],[],[],[],[],[],[]
m_neardai=[]

#ダミー変数を作成するところでdrop_frist=trueとしたため"ほぼ台形"は別で計算
bukken_dummy_shape=pd.get_dummies(bukken["land_shape"])
m_neardai = bukken2["minute_to_station"]*bukken_dummy_shape["ほぼ台形"]

categori = ["land_shape_ほぼ長方形","land_shape_不整形","land_shape_長方形",
            "land_shape_ほぼ正方形","land_shape_ほぼ整形","land_shape_台形",
            "land_shape_正方形","land_shape_袋地等"]

land_shapelist = [m_neartyo,m_hu,m_tyo,m_nearsei,m_nearseikei,m_dai,m_sei,huku]

for i in range (len(land_shapelist)):
    land_shapelist[i] = bukken2["minute_to_station"]*bukken2[categori[i]]

bukken2=bukken2.assign(m_neardai=m_neardai)
bukken2=bukken2.assign(m_neartyo=land_shapelist[0])
bukken2=bukken2.assign(m_hu=land_shapelist[1])
bukken2=bukken2.assign(m_tho=land_shapelist[2])
bukken2=bukken2.assign(m_nearsei=land_shapelist[3])
bukken2=bukken2.assign(m_nearseikei=land_shapelist[4])
bukken2=bukken2.assign(m_dai=land_shapelist[5])
bukken2=bukken2.assign(m_sei=land_shapelist[6])
bukken2=bukken2.assign(m_huku=land_shapelist[7])

assignのところをもう少しシンプルにかければよかったのですがとりあえずこのまま行きます。
残りの説明変数も上記と同様にして、時間との交互作用の積を作っていきます。

すべて作り終わったら全部データとして含まれているか確認します。

.py

bukken2.head()

5×62culumnsとなって入れば大丈夫です。

最後にtrainとtestを元に戻してデータの前処理は終了です。

.py

#trainとtestに戻す
bukken_train2 = bukken2.iloc[:len(bukken_train),:]
bukken_test2 = bukken2.iloc[len(bukken_train):,:]

結果

それでは、交互作用の結果を確認してみましょう。有意性を確認したいので今回はstatsmodelsというライブラリを使うことにします。
statsmodelsについて知りたい方は以下のサイトを参考にしてみてください。

• statsmodelsで回帰分析入門

.py

import statsmodels.api as sm

#説明変数から使わないidと目的変数であるprice_per_tsuboを消去
x_train = bukken_train2.drop(["id","price_per_tsubo"],axis=1)
y_train = bukken_train2["price_per_tsubo"]

model = sm.OLS(y_train,sm.add_constant(x_train))
results = model.fit()
print(results.summary())

変数	coef	t	p>abs(t)
minute_to_station	8825.9778	2.634	0.009
land_space	-274.4973	-3.919	0.000
frontage_length	2733.0440	0.955	0.340
frontal_road_direction_北東	-138.7423	-0.002	0.998
m_shi（時間×市道）	-7312.5120	-2.909	0.004
m_dou（時間×道路）	-6953.2863	-2.327	0.021
m_east（時間×東）	494.3033	0.434	0.664
m_kukaku（時間×区画道路）	-3.749e+04	-0.794	0.428

流石に全部乗っけると長すぎるので代表して何個か表示しています。p>abs(t)はp>|t|ということです(markdownの表の仕様上||が使えませんでした)。
この表を見ると「駅からの時間」などは、相関行列から予想したとおり有意性を持っています。逆に、「間口の長さ」などは、有意性を持ってはいませんでした。交互作用の項においてもそれぞれ、有意性があるかないかを確認することができました。
余談なのですが、データセットに含まれている「道路」があるのに、市道などを分ける必要があるのかなと感じました。（恐らく、道路の種類がわからない用に用意したのかな...）

ついでに"お取り物件"を検出してみましょう。ちなみにお取り物件とは不動産情報で公開されているものの実際に借りることができない物件のことです。一般的に異様に値段が安いというような特徴が挙げられます。今回はその特徴に注目してデータからお取り物件の検出を行います。
ここで、sklearnのlinear_modelを使用していますが、こちらでもt値やp値を算出することは可能です。ただし、式を自分でプログラムする必要があるので少し面倒にはなります。一応以下のサイトを参考にすればできると思うので試したい方は試してみてください。

• 回帰分析のt値の求め方:Pythonで実装
• scikit-learnのLinearRegressionでp値（有意性）を求める

.py

from sklearn import linear_model
model = linear_model.LinearRegression()

model.fit(x_train,y_train)

x_test = bukken_test2.drop(["id","price_per_tsubo"],axis=1)
y_pred = model.predict(x_test)
bukken_test2=bukken_test2.assign(pred=y_pred)

予想された値段と実際の値段を比較するため実際の値段との差を計算します。

.py

err=[]
err=bukken_test2["pred"]-bukken_test2["price_per_tsubo"]

bukken_test2 = bukken_test2.assign(err=err)

#正規化する
hyozyun=[]
hyozyun = (bukken_test2["err"]-bukken_test2["err"].mean())/bukken_test2["err"].std()

bukken_test2 = bukken_test2.assign(hyozyun=hyozyun)

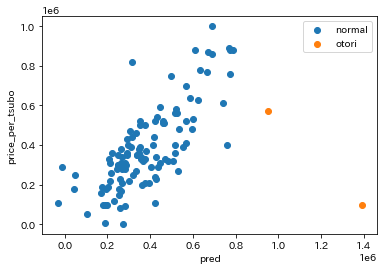
閾値を決めて正規化した値から"お取り物件"と"普通の物件"を分け、散布図に表示してみます。

.py

bukken_test2["flg"]=np.where(bukken_test2["hyozyun"]>=2,"otori","normal")
flg,ax=plt.subplots(1)
plt.scatter(data = bukken_test2.query("flg == 'normal'"), x = "pred", y = "price_per_tsubo",  label = "normal")
plt.scatter(data = bukken_test2.query("flg == 'otori'"), x = "pred", y = "price_per_tsubo",  label = "otori")
plt.xlabel("pred")
plt.ylabel("price_per_tsubo")
ax.legend()

お取り物件の情報を見てみます。

.py

otori_id=bukken_test2.query("flg=='otori'")[["id"]]
pd.merge(bukken_test,otori_id,on="id")

お取り物件の情報は一部しか表示していませんが、それらしきものを得られることはできました。
他の変数の交互作用を考慮すればさらに精度が高まる気がします。

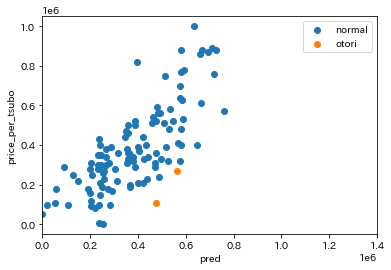
交互作用がない場合も比較として表示してみます。

見比べて見ると、交互作用がある方が散布図にはっきりと現れていることが分かると思います。お取り物件として予想されたデータも他のデータと相関が近く、偶然選ばれた印象を受けました。
実際、データをどう判断するかは人によりけりだとは思いますが、個人的には交互作用を考慮したほうが予想値に信憑性が持てる気がします。

最後に

交互作用は統計的に有意であるなどを考えなくてはいけませんでした。データサイエンティストになりたい人は避けては通れない道ですし、それ以外の人も知識として知っておくだけでもどこかで約に立つかもしれないです。(以外の知っている人がいないのでww)
最近自分の研究室の先生が「t検定をしてみる？」とずっと言っているため、自分も本格的にt検定の勉強をしているところです。

追伸

qiitaの表を使ってデータを表示したかったのですが、億劫になって画像を貼り付けだけで済ませてしまいました...。