- はじめに
この記事では、前回紹介した方法で作成した解析用構造格子を自作のFDM(有限差分法)ソルバーに投げ込み、最終的な計算結果をParaViewで可視化するまでを書いてみます。
なお、FDMの具体的な数値計算手法は他の文献に譲ります。それほど難しくないので興味のある方は勉強されてみるといいかもしれません。
また、一連の処理を行うソースコードはC++で書いています。読みづらいかと思いますが許してください。
あと記事が長くなりすぎないように、メインの処理以外のソースコードは省略しております。
ソースコードが欲しい方はここからどうぞ。煮るなり焼くなり好きにしてください。
- 大まかな処理の流れ
今回開発したプログラムは以下のようなフローで実行されます。
まず閉曲面ポリゴンを構造格子ジェネレーターに入力し、その後解析用の属性をボクセルに付与してソルバーに投げ込んであげると数値計算が始まります。ソルバーでの解析が終わった後はVTKファイルで計算結果が出力されますので、ParaView等で内容を詳しく見ることができます。
また、フロー中における青い部分はモジュール化されてますので、それぞれ単独でも使えるようになっています。

メインの処理を記述したソースコードを以下に示します。
# include "vtkVoxelMeshGenerator.h"
# include "vtkSettingAnalyticProperties.h"
# include "FDMSolverForDiffusionEq.h"
# include <iostream>
# include <memory>
# include <vtkGeometryFilter.h>
# include <vtkUnstructuredGrid.h>
// Reader & Writer
# include <vtkDataSetReader.h>
# include <vtkSTLReader.h>
# include <vtkDataSetWriter.h>
# include <vtkXMLDataSetWriter.h>
using namespace std;
int main()
{
// 閉曲面読み取り
auto reader = vtkSmartPointer<vtkDataSetReader>::New();
reader->SetFileName("C:\\test\\bunny.vtk");
reader->Update();
// PolyDataに変換
auto geometry = vtkSmartPointer<vtkGeometryFilter>::New();
geometry->SetInputData(reader->GetOutput());
geometry->Update();
cout << "ボクセルメッシュ作成" << endl;
const int cellDims[] = { 60, 60, 60 };
const double *bounds = geometry->GetOutput()->GetBounds();
const double offsetX = (bounds[1] - bounds[0]) * 0.2;
const double offsetY = (bounds[3] - bounds[2]) * 0.2;
const double offsetZ = (bounds[5] - bounds[4]) * 0.2;
const double offsets[6] = { offsetX, offsetX, offsetY, offsetY, offsetZ, offsetZ };
// スマートポインタでインスタンスを管理
shared_ptr<vtkVoxelMeshGenerator> voxelMeshGenerator = make_shared<vtkVoxelMeshGenerator>();
voxelMeshGenerator->SetInputData(geometry->GetOutput());
voxelMeshGenerator->SetCellDimensions(cellDims);
voxelMeshGenerator->SetOffsets(offsets);
voxelMeshGenerator->Update();
cout << "ボクセルメッシュに解析属性を付与" << endl;
shared_ptr<vtkSettingAnalyticProperties> analyticProperties;
analyticProperties = make_shared<vtkSettingAnalyticProperties>();
analyticProperties->SetCellDimensions(cellDims);
analyticProperties->SetInputData(voxelMeshGenerator->GetOutput());
analyticProperties->Update();
auto field = vtkSmartPointer<vtkUnstructuredGrid>::New();
field->DeepCopy(analyticProperties->GetOutput());
cout << "解析開始" << endl;
const double alpha = 0.1;
const double wallXYZBC[3] = { 10.0, 100.0, 40.0 };
const int endStep = 2000;
shared_ptr<FDMSolverForDiffusionEq> solver;
solver = make_shared<FDMSolverForDiffusionEq>();
solver->SetAlpha(alpha);
solver->SetWallXYZBC(wallXYZBC);
solver->SolveHeatEquationForAllStep(field, endStep);
auto writer = vtkSmartPointer<vtkXMLDataSetWriter>::New();
writer->SetFileName("C:\\test\\Results.vtu");
writer->SetInputData(field);
writer->Update();
return 0;
}
- 構造格子生成
前回の記事で作ったプログラムを拡張して構造格子を生成します。変更点は以下の通りです。
- 3Dモデル(閉曲面ポリゴン内のボクセル)かどうかの情報をボクセル単位で保持し、"Is3DModel" という配列で管理する。
- ボクセルの通し番号をボクセル単位で保持し、"OriginalVoxelId" という配列で管理する。
- ベースの構造格子の境界を拡張できるようにする。
構造格子生成プログラムのソースコードはこちらとこちらから読めます。
プログラムによって作成したボクセルメッシュをParaView上で読み込み、コンター図を "Is3DModel" に設定し断面を見ると次のように表示されます。
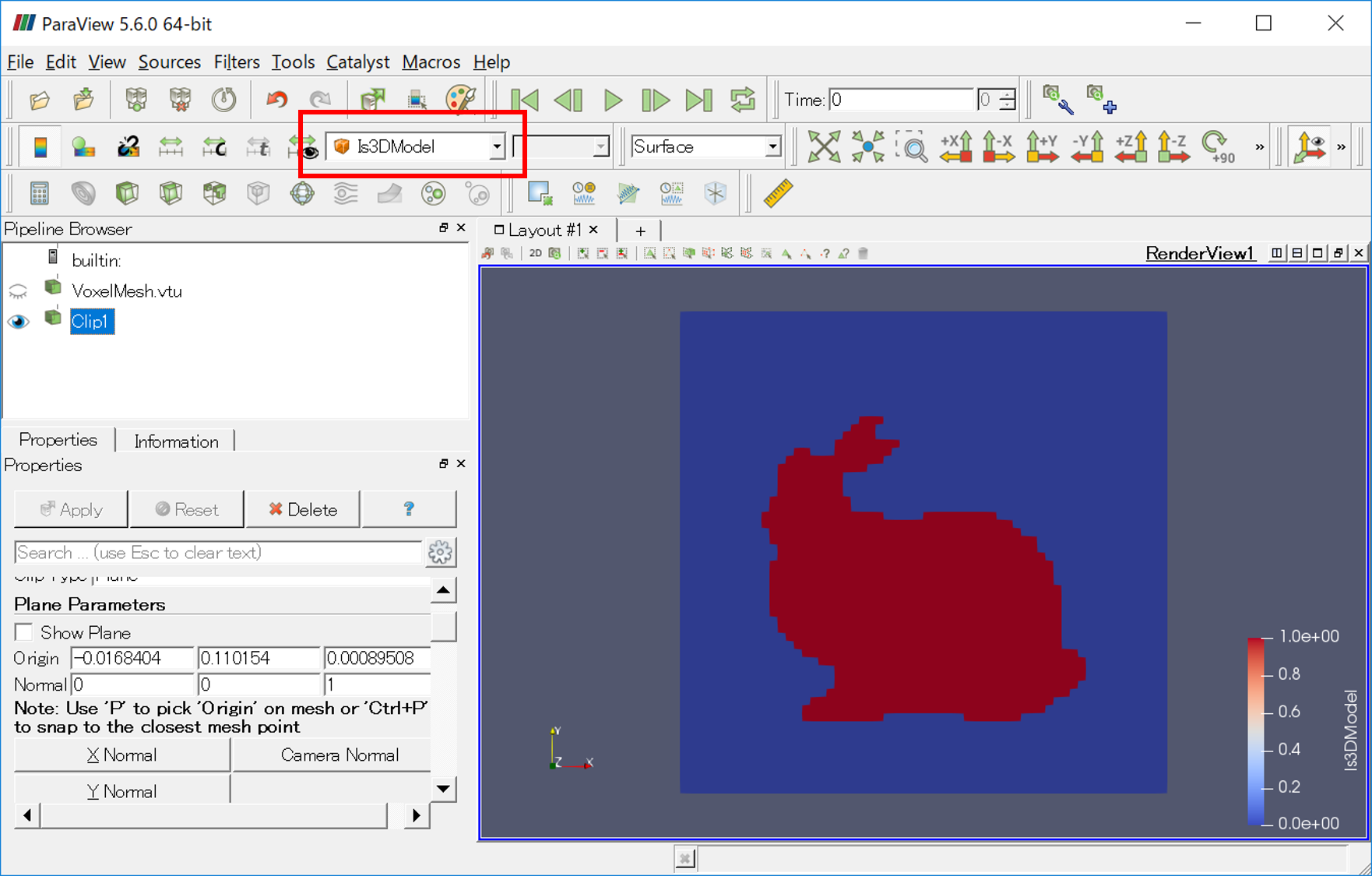
- 各ボクセルに解析用の属性を付与
境界条件などを与えるボクセルを簡単に識別するために、ボクセル単位で解析用の属性をつけてあげます。
なお、ソースコード中では "AnalyticProperty" という配列で管理しています。
今回は、以下のような属性をボクセルに付与しています。
- 3Dモデルの表面:周辺のボクセルに定義されている物理量(拡散物質の密度)の平均値をとる。
- 3Dモデルの内側:解析しない。
- 壁面:座標軸の方向別にそれぞれ定数値を定義する。
- 上記以外:偏微分方程式を離散化した式で解析を行う。
プログラムによって情報を追加したボクセルメッシュをParaView上で読み込み、コンター図を "AnalyticProperpy" に設定し断面を見ると次のように表示されます。
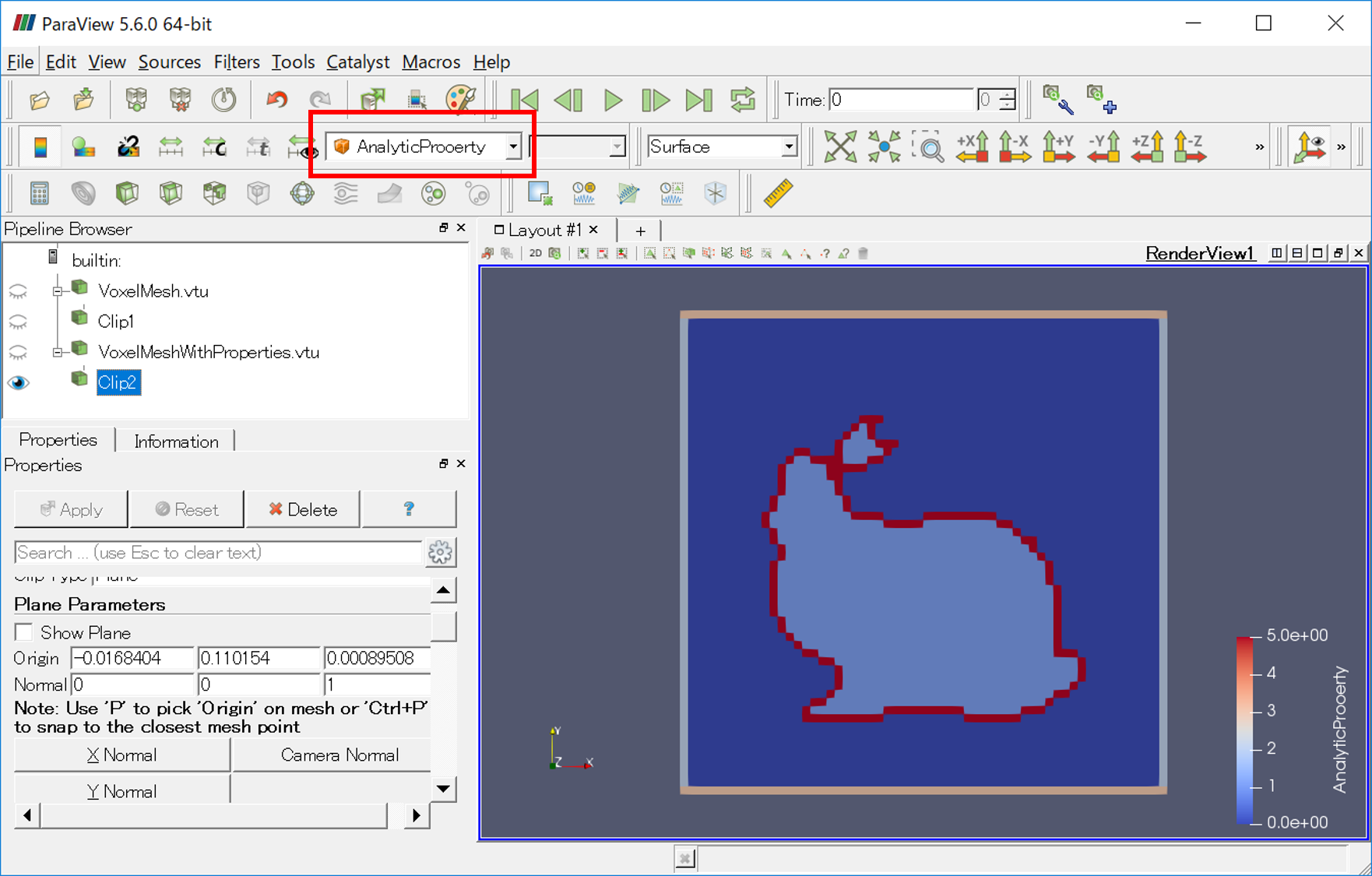
壁面、3Dモデル表面・内部、その以外のボクセルに番号が与えられており、それぞれをプログラム中で識別できるようになっています。
- 解析
生成した解析用メッシュに対し、自作のFDMソルバーで解析します。
なお、今回は取り扱うのは以下のような拡散方程式です。
\frac{\partial u}{\partial t} = \alpha \nabla^2 u
初期条件は全領域における拡散物質の密度を0とし、指定した計算ステップまで計算させます。
u|_{t=0} = 0
- 可視化
解析終了後、ソルバーからVTKのXML形式で解析結果が出力されるので、これをParaViewへドラッグ&ドロップし、[Apply] ボタンを押すと次のように計算結果が表示されます。
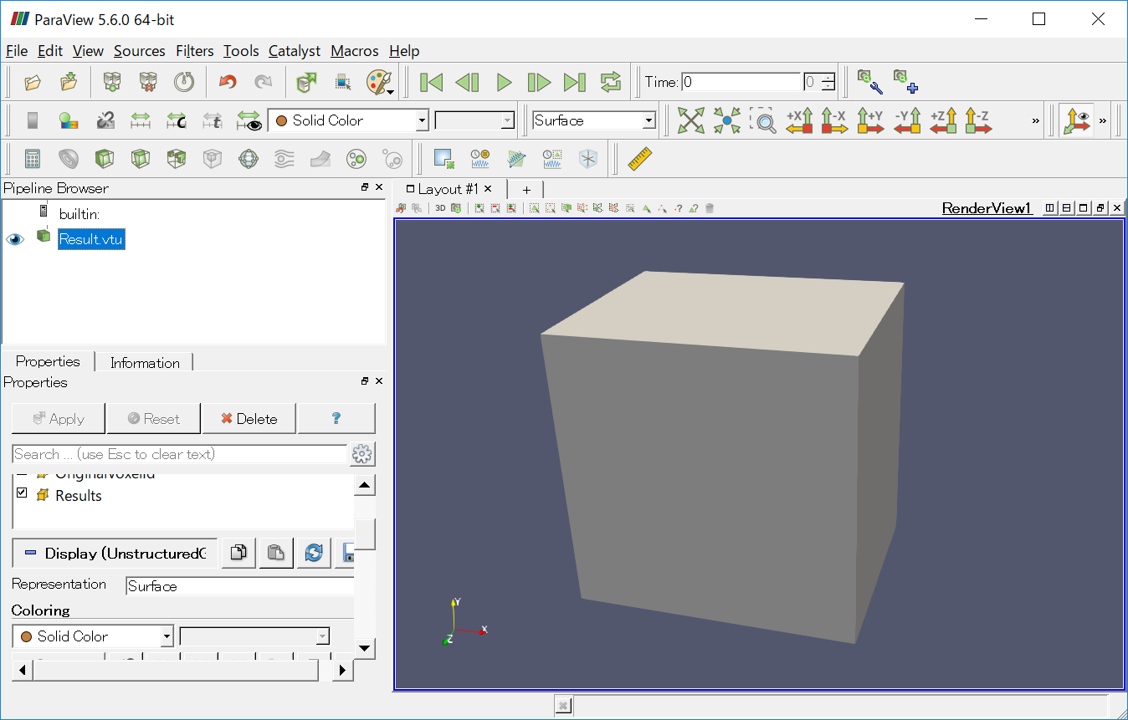
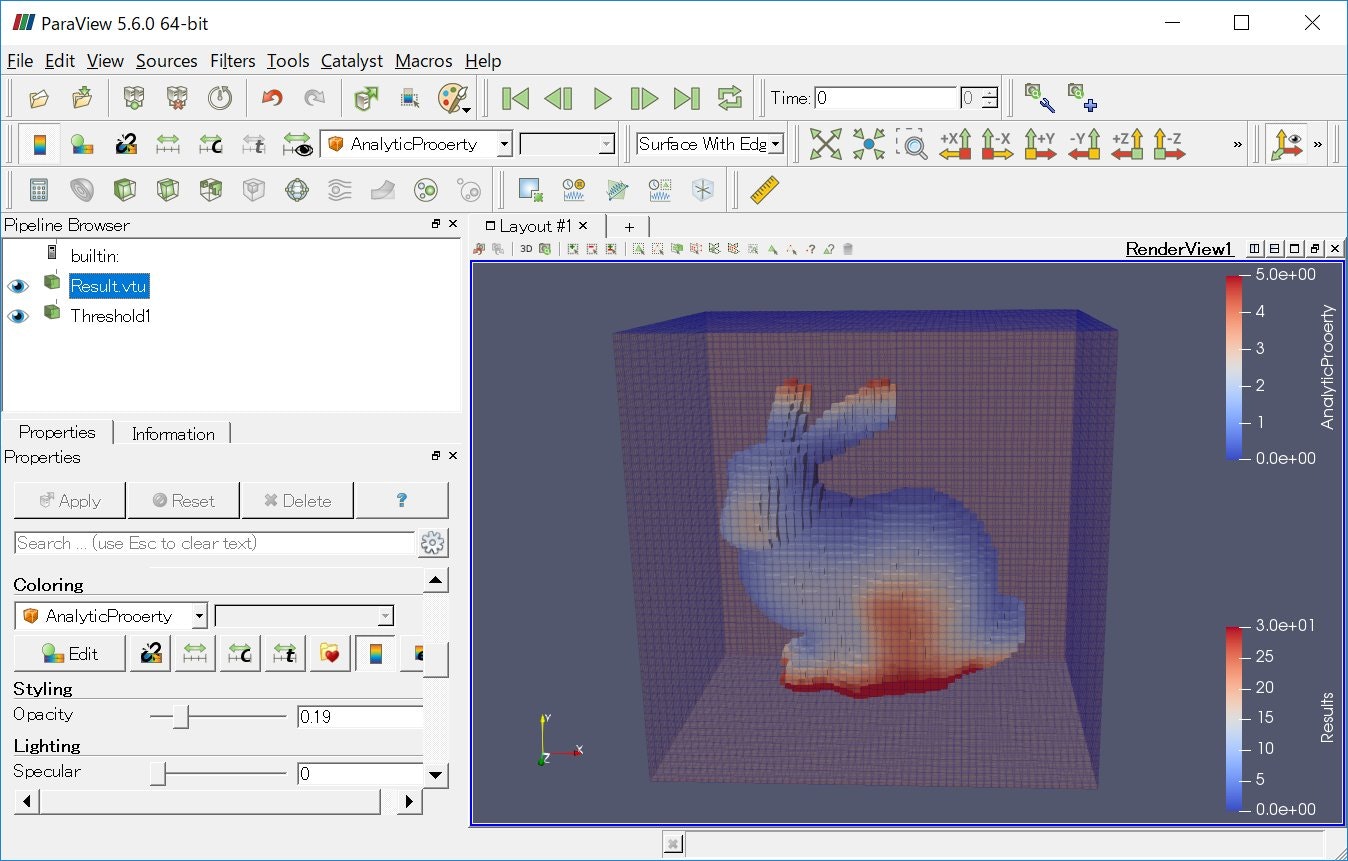
このままだとよくわからないので、[Filter] -> [Alphabetical] -> [threshold] を選択し、[Properties]タブ内の [Scalars] から "Is3DModel" を選択し、[Minimum] と [Maximum] をそれぞれ1にして [Apply] を押します。
ウサギさんが出てきました![]()
次に計算結果を色付きで見るために、コンターの表示を "Results" に変更します。
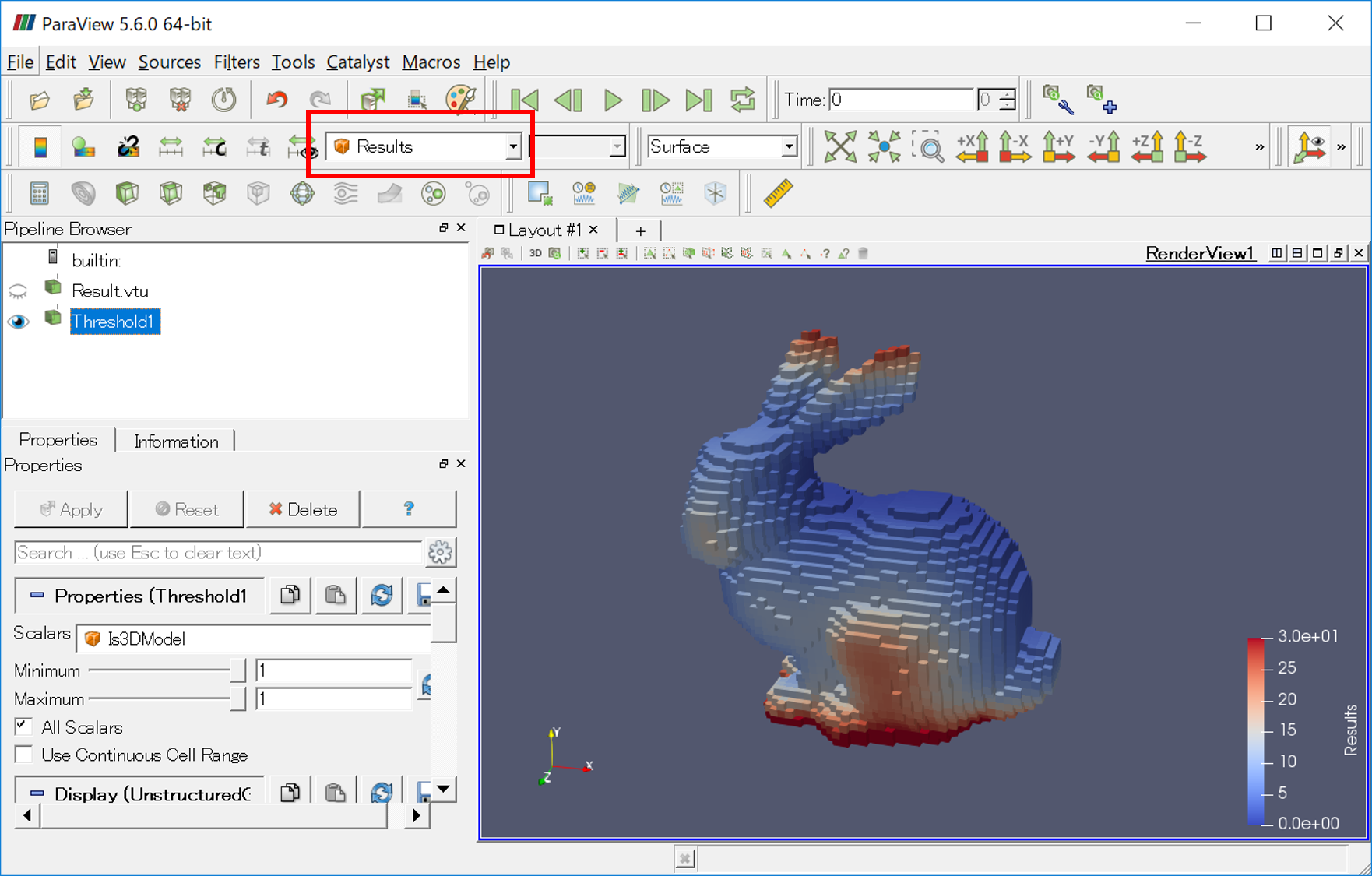
ウサギさんにちゃんと色がついてますね!
アニメーション
- おわりに
VTKで作った構造格子をソルバーに投げ込んで計算したものをParaViewで可視化してみました。
今回は拡散方程式を解きましたが、これを流体の方程式に置き換え、入力する3Dモデルを障害物として解析してみても面白いかもしれません。
また、ソースコード中での疑問があればコメントを投稿していただければ幸いです。
