Stop Words とは多くの文書に含まれていてそれ自体が文書の特徴を表しづらい単語を表します。例えば英文における the や in, after といったような単語は典型的な Stop Words です。
このような単語は検索時にノイズの原因となるためあらかじめ検索対象から除外する必要があります。この記事は**選択情報量** (自己エントロピー) を使って検索時に除外すべき Stop Words を判断するための指標を求めます。
なおここで扱っている数式は TF-IDF でいうところの DF (Document Frequency) と本質的に同じです。情報量/エントロピーが「文書集合全体」に対する単語の特徴を示すのに対して、TF-IDF は「ある文書」に対する単語の特徴を示す (目的は文書要約や代表語の抽出) という点で異なります。
情報量とエントロピーの求め方
選択情報量
総文書数 $N$ の文書集合において単語 $W$ を含む文書数を $n_w$ とした場合、$W$ が文書に含まれる確率 $P_{(W)}$ は以下のように表される。
$P_{(W)} = \frac{n_w}{N}$
このとき、単語 $W$ に対する選択情報量 $I_{(W)}$ は以下のように表される。
$I_{(W)} = \log \frac{1}{P_{(W)}} = \log N - \log n_w$
どの文書にも含まれない単語 ($n_w=0$, すなはち $P_{(0)}=0$) の情報量は $I = \infty$ と発散するため対象外とします。$I_{(W)}$ について対数の底をどう取っても本質的な差はないことから、底を総文書数 $N$ とすると:
$I_{(W)} = \log_N N - \log_N n_w = 1 - \log_N n_w = 1 - \frac{\log n_w}{\log N}$
条件 $1 \le n_w \le N$ より $0 \le I_{(W)} \le 1$ の範囲となり実用的な指標として使いやすくなりますの本記事ではこの式を使用します。
以上より、例えば全ての文書に含まれる特徴の無い単語は $n_w = N$ より $I_{(W)}=0$ となるため、$I_{(W)}$ が $0$ に近い単語 $W$ は特徴の無い Stop Words と判断できます。
同様に、一つの文書にしか含まれない単語は $n_w = 1$ であることから $I_{(W)}=1$ に近い近い単語は文書集合全体で特徴的な単語と判断できます。ただしきわめて少数の文書にしか出現しない単語は実際には死語や造語の可能性が高いため排除対象として考慮する必要があります。
平均情報量
文書集合全体の 平均情報量 (エントロピー) は以下のように表されます。
$H_{(P)} = - \sum P \log P = - \sum \frac{n_w}{N} ( \log n_w - \log N)$
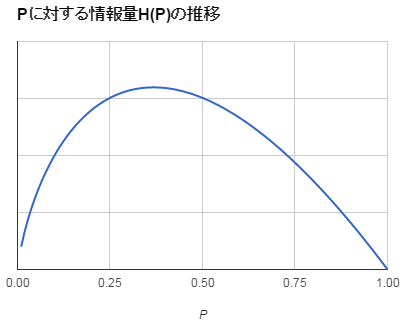
固定値とした $P$ に対して $H_{(P)}$ は以下のようなふるまいをとります (単調増加/単調減少ではないため自己情報量のように対数の底を $N$ とするのは止めておきましょう)。
エントロピーが低い文書集合は単語の分布に偏りや均一さなどの規則性が高いと言えます。もう少しかみ砕くと、文書ごとに特色やテーマがはっきりしていてカテゴリライズがうまく機能しているか、あるいは似たような内容の文書ばかりと解釈できます。これは文書集合全体の品質指標として使えるでしょう。