はじめに
近年AIが隆盛していますが、AIではまだ実現不可能な領域の勉強をしたく数理最適化に着目しました。
ナップサック問題、巡回セールスマン問題などに代表される組み合わせ最適化問題ですが、ビジネスでも私生活でも組み合わせ最適化問題は身近にあり、それを解けるようになることでスキルアップに繋がると考えました。
そんな流れで数理最適化勉強中の身ですので、誤りなどありましたらご指摘お願いします。
目的
私の趣味である音楽ゲーム ダンスダンスレボリューション(以下、DDR)で最適な足運びを模索したいと思います。
DDRについて
画面に矢印が流れてくるので、リズムに合わせて矢印を踏むゲームです。
30年前くらいに大流行をしましたが、今現在でもプレイヤーも多くまだまだ活気はあります。
私も引きこもりがちな人間で何かで運動しないといけないなと思い、長続きしそうなゲームに運動要素があるDDRに着目したらドハマりしました。
そんなDDRですが、難易度が高くなるとかなり疲れます。以下に(私ではなく、よそ様の)DDRのプレイ動画を貼っていますが、かなりの密度で矢印が流れてくると思います。
これを考え無しに踏んでいると疲れるので、この踏む順番を数理最適化で解こうといった趣旨になります。
数理最適化について
「組み合わせ最適化問題 サービス 無料」で調べて出てきた中で、チュートリアルが豊富で、無料枠があるFixstars Amplifyを使うことにしました。
特にチュートリアルにある巡回セールスマン問題をこんなにもシンプルに、こんなにも早く解けるとは思っていなかったので、正直驚きました。
数理最適化凄い・・・!
DDRの定式化
ここからは上記のチュートリアルを理解出来ている前提で話を進めます。
今回は「最適な足運びを模索する」のが目標なので、足の移動量が少なくなる足運びを求めることにします。
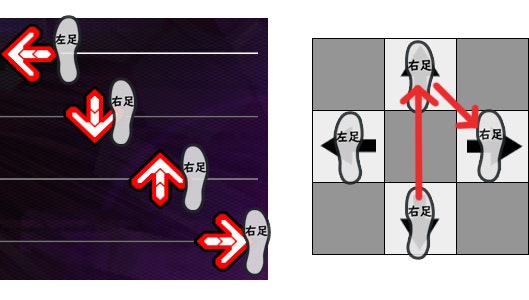
以下のような矢印が流れてきたときに最短な踏み方はどうでしょうか?

このようにいろいろなパターンが考えられると思いますが、全パターンの中で最短を求めたいと思います。
パターン数は、左右の足のどちらで踏むかを矢印の数だけ区別するので 2^矢印の数 になります。
莫大なパターンになるため、組み合わせ最適化問題と同じ要領で解く必要がありそうですね。
定式化する上での条件
- DDRには同時に2つの矢印を踏むケースがあるが、それは無いものとする。
- DDRには足の動きによって後ろ向きになったり回転することがあるが、腰は無限に回り、後ろ向きや回転などは無いものとする。
- DDRではなるべく左右の足で交互に矢印を踏むのが良いとされるが、それは考慮しない。
定式化
決定変数は「n番目のステップでそれぞれの足がどこにあるかを表す」ように設定しました。
矢印1番目の時に左足がq0~q3のどこにあるかを示す。1になっている場所に左足があるとする。
同様に、矢印1番目の時に右足がq4~q7のどこにあるかを示す。1になっている場所に右足があるとする。
これを全矢印に対して決定変数を作成します。
例
左足、右足を交互に動かすパターンを決定変数で表すと以下のようになります。

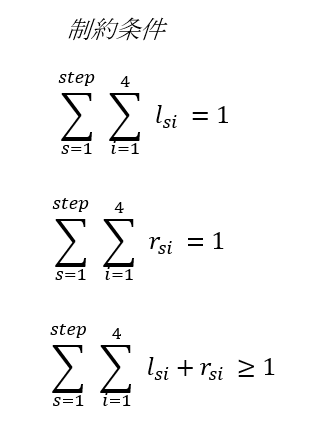
制約条件
以下の2つの制約を設定します
制約条件①各足は1か所しか踏めない
各足の範囲にone_hot制約を付けます。
こうすることで、左足は1か所しか踏めず、右足も1か所しか踏めない状態になります。
制約条件②指定された箇所を1か所以上踏む
矢印に対して、各足の踏む位置にgreater_equal制約を付けます。
こうすることで流れてきた矢印を左右のどちらかの足で踏んでいる状態になります。
目的関数
足の移動量が少なくなる足運びを目的関数にします。
DDRのパネルの距離感は以下のようになっています。
斜めに足を動かす場合の移動量は72cm、対面に動かす場合の移動量は102cmです。(ゲームセンターで計測してきました)

各足の位置からの移動量を最小化するためには、各足の移動パターンをすべて加算することで求めることが出来ます。
左足の1番目の矢印が←だった時に、2番目の矢印に移動する時の移動量は以下のようになります。
←だった場合、 ←から←なので移動量は0
↓だった場合、 ←から↓なので移動量は72
↑だった場合、 ←から↑なので移動量は72
→だった場合、 ←から→なので移動量は102
これを決定変数で表す場合
(q0 * q8 * 0) + (q0 * q9 * 72) + (q0 * q10 * 72) + (q0 * q11 * 102)となります。
このように、各足から各足への全パターンを決定変数に組み込むことで、最短移動量の足の移動が導けるはずです。
数式
あんまり数式書いてこなかったので間違えているかもしれませんが、数式で表していることが多いので私も挑戦してみました。
上記の説明を数式にしたのがこれだと思います。(自信はありません)
実装
基本的にチュートリアルにある関数だけで作れました。
必要モジュール
pip install numpy
pip install amplify
インポート
from typing import Literal, List
import numpy as np
from amplify import (
FixstarsClient,
VariableGenerator,
equal_to,
greater_equal,
one_hot,
solve,
Poly,
ConstraintList,
Constraint
)
from datetime import date, timedelta, datetime
from dataclasses import dataclass, field
import matplotlib.pyplot as plt
クライアントの設定
# クライアントの設定
client = FixstarsClient()
client.parameters.timeout = timedelta(milliseconds=10*1000)
client.token = "AE/xxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
client.parameters.outputs.num_outputs = 0
np.set_printoptions(threshold=np.inf)
パネルの設定
import collections
from math import sqrt # import sqrt function from math module
PanelPosition = collections.namedtuple('PanelPosition', ['x', 'y'])
# 上記のようにパネルを踏む箇所を定義する。 0が← 1が↓ 2が↑ 3が→ とする。
# パネルの踏む位置
panel_pos = [
PanelPosition(-51, 0),
PanelPosition(0, -51),
PanelPosition(0, 51),
PanelPosition(51, 0),
]
def panel_from_to_dist(from_val, to_val):
return int(sqrt(pow(from_val.x - to_val.x, 2) + pow(from_val.y - to_val.y, 2)))
panel_from_to_dist(panel_pos[0],panel_pos[1])
# panel_posにある各要素から各要素への距離を求め、それをリストに格納する
panel_from_to_dist_list = [[ panel_from_to_dist(p1,p2) for p2 in panel_pos ] for p1 in panel_pos ]
#print(panel_from_to_dist_list)
print(f"←から←への足の移動量 : {panel_from_to_dist_list[0][0]}")
print(f"←から↓への足の移動量 : {panel_from_to_dist_list[0][1]}")
print(f"←から↑への足の移動量 : {panel_from_to_dist_list[0][2]}")
print(f"←から→への足の移動量 : {panel_from_to_dist_list[0][3]}")
←から←への足の移動量 : 0
←から↓への足の移動量 : 72
←から↑への足の移動量 : 72
←から→への足の移動量 : 102
矢印の定義
# 流れてくる矢印を以下のように表す
notes = [
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1],
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1],
]
print(len(notes))
total_notes = len(notes)
# 左足は ←を踏んだ状態でスタートする
# 右足は →を踏んだ状態でスタートする
start_left_foot_pos = 0
start_right_foot_pos = 3
決定変数の作成
gen = VariableGenerator()
gantt = gen.array(
"Binary", shape=(total_notes, len(panel_pos)*2)
)
print(gantt)
from amplify import sum
[[q_{0,0}, q_{0,1}, q_{0,2}, q_{0,3}, q_{0,4}, q_{0,5}, q_{0,6}, q_{0,7}],
[q_{1,0}, q_{1,1}, q_{1,2}, q_{1,3}, q_{1,4}, q_{1,5}, q_{1,6}, q_{1,7}],
[q_{2,0}, q_{2,1}, q_{2,2}, q_{2,3}, q_{2,4}, q_{2,5}, q_{2,6}, q_{2,7}],
[q_{3,0}, q_{3,1}, q_{3,2}, q_{3,3}, q_{3,4}, q_{3,5}, q_{3,6}, q_{3,7}],
[q_{4,0}, q_{4,1}, q_{4,2}, q_{4,3}, q_{4,4}, q_{4,5}, q_{4,6}, q_{4,7}],
[q_{5,0}, q_{5,1}, q_{5,2}, q_{5,3}, q_{5,4}, q_{5,5}, q_{5,6}, q_{5,7}],
[q_{6,0}, q_{6,1}, q_{6,2}, q_{6,3}, q_{6,4}, q_{6,5}, q_{6,6}, q_{6,7}],
[q_{7,0}, q_{7,1}, q_{7,2}, q_{7,3}, q_{7,4}, q_{7,5}, q_{7,6}, q_{7,7}]]
制約条件①
# 1つのレーンで、踏むのは片足のどちらかのみ
constarints_1 = ConstraintList()
for lane in range(total_notes):
constarints_1 += one_hot(gantt[lane][0:4])
constarints_1 += one_hot(gantt[lane][4:8])
print(constarints_1)
[q_{0,0} + q_{0,1} + q_{0,2} + q_{0,3} == 1 (weight: 1),
q_{0,4} + q_{0,5} + q_{0,6} + q_{0,7} == 1 (weight: 1),
q_{1,0} + q_{1,1} + q_{1,2} + q_{1,3} == 1 (weight: 1),
q_{1,4} + q_{1,5} + q_{1,6} + q_{1,7} == 1 (weight: 1),
q_{2,0} + q_{2,1} + q_{2,2} + q_{2,3} == 1 (weight: 1),
q_{2,4} + q_{2,5} + q_{2,6} + q_{2,7} == 1 (weight: 1),
q_{3,0} + q_{3,1} + q_{3,2} + q_{3,3} == 1 (weight: 1),
q_{3,4} + q_{3,5} + q_{3,6} + q_{3,7} == 1 (weight: 1),
q_{4,0} + q_{4,1} + q_{4,2} + q_{4,3} == 1 (weight: 1),
q_{4,4} + q_{4,5} + q_{4,6} + q_{4,7} == 1 (weight: 1),
q_{5,0} + q_{5,1} + q_{5,2} + q_{5,3} == 1 (weight: 1),
q_{5,4} + q_{5,5} + q_{5,6} + q_{5,7} == 1 (weight: 1),
q_{6,0} + q_{6,1} + q_{6,2} + q_{6,3} == 1 (weight: 1),
q_{6,4} + q_{6,5} + q_{6,6} + q_{6,7} == 1 (weight: 1),
q_{7,0} + q_{7,1} + q_{7,2} + q_{7,3} == 1 (weight: 1),
q_{7,4} + q_{7,5} + q_{7,6} + q_{7,7} == 1 (weight: 1)]
制約条件②
# 指定された矢印を踏む
constarints_2 = ConstraintList()
for i, lane in enumerate(notes):
if lane[0] == 1:
constarints_2 += greater_equal(gantt[i][0] + gantt[i][4], 1)
if lane[1] == 1:
constarints_2 += greater_equal(gantt[i][1] + gantt[i][5], 1)
if lane[2] == 1:
constarints_2 += greater_equal(gantt[i][2] + gantt[i][6], 1)
if lane[3] == 1:
constarints_2 += greater_equal(gantt[i][3] + gantt[i][7], 1)
print(constarints_2)
[q_{0,0} + q_{0,4} >= 1 (weight: 1),
q_{1,1} + q_{1,5} >= 1 (weight: 1),
q_{2,2} + q_{2,6} >= 1 (weight: 1),
q_{3,3} + q_{3,7} >= 1 (weight: 1),
q_{4,0} + q_{4,4} >= 1 (weight: 1),
q_{5,1} + q_{5,5} >= 1 (weight: 1),
q_{6,2} + q_{6,6} >= 1 (weight: 1),
q_{7,3} + q_{7,7} >= 1 (weight: 1)]
左足の目的関数
left_objective = 0
for n, note1 in enumerate(notes):
for current in range(4):
if n != 0:
for pre in range(4):
dist = panel_from_to_dist_list[pre][current]
left_objective += gantt[n-1][pre] * gantt[n][current] * dist
else :
dist = panel_from_to_dist_list[start_left_foot_pos][current]
left_objective += gantt[n][current] * dist
print(left_objective)
72 q_{0,0} q_{1,1} + 72 q_{0,0} q_{1,2} + 102 q_{0,0} q_{1,3} + 72 q_{0,1} q_{1,0} + 102 q_{0,1} q_{1,2} + 72 q_{0,1} q_{1,3} + 72 q_{0,2} q_{1,0} + 102 q_{0,2} q_{1,1} + 72 q_{0,2} q_{1,3} + 102 q_{0,3} q_{1,0} + 72 q_{0,3} q_{1,1} + 72 q_{0,3} q_{1,2} + 72 q_{1,0} q_{2,1} + 72 q_{1,0} q_{2,2} + 102 q_{1,0} q_{2,3} + 72 q_{1,1} q_{2,0} + 102 q_{1,1} q_{2,2} + 72 q_{1,1} q_{2,3} + 72 q_{1,2} q_{2,0} + 102 q_{1,2} q_{2,1} + 72 q_{1,2} q_{2,3} + 102 q_{1,3} q_{2,0} + 72 q_{1,3} q_{2,1} + 72 q_{1,3} q_{2,2} + 72 q_{2,0} q_{3,1} + 72 q_{2,0} q_{3,2} + 102 q_{2,0} q_{3,3} + 72 q_{2,1} q_{3,0} + 102 q_{2,1} q_{3,2} + 72 q_{2,1} q_{3,3} + 72 q_{2,2} q_{3,0} + 102 q_{2,2} q_{3,1} + 72 q_{2,2} q_{3,3} + 102 q_{2,3} q_{3,0} + 72 q_{2,3} q_{3,1} + 72 q_{2,3} q_{3,2} + 72 q_{3,0} q_{4,1} + 72 q_{3,0} q_{4,2} + 102 q_{3,0} q_{4,3} + 72 q_{3,1} q_{4,0} + 102 q_{3,1} q_{4,2} + 72 q_{3,1} q_{4,3} + 72 q_{3,2} q_{4,0} + 102 q_{3,2} q_{4,1} + 72 q_{3,2} q_{4,3} + 102 q_{3,3} q_{4,0} + 72 q_{3,3} q_{4,1} + 72 q_{3,3} q_{4,2} + 72 q_{4,0} q_{5,1} + 72 q_{4,0} q_{5,2} + 102 q_{4,0} q_{5,3} + 72 q_{4,1} q_{5,0} + 102 q_{4,1} q_{5,2} + 72 q_{4,1} q_{5,3} + 72 q_{4,2} q_{5,0} + 102 q_{4,2} q_{5,1} + 72 q_{4,2} q_{5,3} + 102 q_{4,3} q_{5,0} + 72 q_{4,3} q_{5,1} + 72 q_{4,3} q_{5,2} + 72 q_{5,0} q_{6,1} + 72 q_{5,0} q_{6,2} + 102 q_{5,0} q_{6,3} + 72 q_{5,1} q_{6,0} + 102 q_{5,1} q_{6,2} + 72 q_{5,1} q_{6,3} + 72 q_{5,2} q_{6,0} + 102 q_{5,2} q_{6,1} + 72 q_{5,2} q_{6,3} + 102 q_{5,3} q_{6,0} + 72 q_{5,3} q_{6,1} + 72 q_{5,3} q_{6,2} + 72 q_{6,0} q_{7,1} + 72 q_{6,0} q_{7,2} + 102 q_{6,0} q_{7,3} + 72 q_{6,1} q_{7,0} + 102 q_{6,1} q_{7,2} + 72 q_{6,1} q_{7,3} + 72 q_{6,2} q_{7,0} + 102 q_{6,2} q_{7,1} + 72 q_{6,2} q_{7,3} + 102 q_{6,3} q_{7,0} + 72 q_{6,3} q_{7,1} + 72 q_{6,3} q_{7,2} + 72 q_{0,1} + 72 q_{0,2} + 102 q_{0,3}
右足の目的関数
right_objective = 0
for n, note1 in enumerate(notes):
for current in range(4):
if n != 0:
for pre in range(4):
dist = panel_from_to_dist_list[pre][current]
right_objective += gantt[n-1][4+pre] * gantt[n][4+current] * dist
else :
dist = panel_from_to_dist_list[start_right_foot_pos][current]
right_objective += gantt[n][4+current] * dist
print(right_objective)
72 q_{0,4} q_{1,5} + 72 q_{0,4} q_{1,6} + 102 q_{0,4} q_{1,7} + 72 q_{0,5} q_{1,4} + 102 q_{0,5} q_{1,6} + 72 q_{0,5} q_{1,7} + 72 q_{0,6} q_{1,4} + 102 q_{0,6} q_{1,5} + 72 q_{0,6} q_{1,7} + 102 q_{0,7} q_{1,4} + 72 q_{0,7} q_{1,5} + 72 q_{0,7} q_{1,6} + 72 q_{1,4} q_{2,5} + 72 q_{1,4} q_{2,6} + 102 q_{1,4} q_{2,7} + 72 q_{1,5} q_{2,4} + 102 q_{1,5} q_{2,6} + 72 q_{1,5} q_{2,7} + 72 q_{1,6} q_{2,4} + 102 q_{1,6} q_{2,5} + 72 q_{1,6} q_{2,7} + 102 q_{1,7} q_{2,4} + 72 q_{1,7} q_{2,5} + 72 q_{1,7} q_{2,6} + 72 q_{2,4} q_{3,5} + 72 q_{2,4} q_{3,6} + 102 q_{2,4} q_{3,7} + 72 q_{2,5} q_{3,4} + 102 q_{2,5} q_{3,6} + 72 q_{2,5} q_{3,7} + 72 q_{2,6} q_{3,4} + 102 q_{2,6} q_{3,5} + 72 q_{2,6} q_{3,7} + 102 q_{2,7} q_{3,4} + 72 q_{2,7} q_{3,5} + 72 q_{2,7} q_{3,6} + 72 q_{3,4} q_{4,5} + 72 q_{3,4} q_{4,6} + 102 q_{3,4} q_{4,7} + 72 q_{3,5} q_{4,4} + 102 q_{3,5} q_{4,6} + 72 q_{3,5} q_{4,7} + 72 q_{3,6} q_{4,4} + 102 q_{3,6} q_{4,5} + 72 q_{3,6} q_{4,7} + 102 q_{3,7} q_{4,4} + 72 q_{3,7} q_{4,5} + 72 q_{3,7} q_{4,6} + 72 q_{4,4} q_{5,5} + 72 q_{4,4} q_{5,6} + 102 q_{4,4} q_{5,7} + 72 q_{4,5} q_{5,4} + 102 q_{4,5} q_{5,6} + 72 q_{4,5} q_{5,7} + 72 q_{4,6} q_{5,4} + 102 q_{4,6} q_{5,5} + 72 q_{4,6} q_{5,7} + 102 q_{4,7} q_{5,4} + 72 q_{4,7} q_{5,5} + 72 q_{4,7} q_{5,6} + 72 q_{5,4} q_{6,5} + 72 q_{5,4} q_{6,6} + 102 q_{5,4} q_{6,7} + 72 q_{5,5} q_{6,4} + 102 q_{5,5} q_{6,6} + 72 q_{5,5} q_{6,7} + 72 q_{5,6} q_{6,4} + 102 q_{5,6} q_{6,5} + 72 q_{5,6} q_{6,7} + 102 q_{5,7} q_{6,4} + 72 q_{5,7} q_{6,5} + 72 q_{5,7} q_{6,6} + 72 q_{6,4} q_{7,5} + 72 q_{6,4} q_{7,6} + 102 q_{6,4} q_{7,7} + 72 q_{6,5} q_{7,4} + 102 q_{6,5} q_{7,6} + 72 q_{6,5} q_{7,7} + 72 q_{6,6} q_{7,4} + 102 q_{6,6} q_{7,5} + 72 q_{6,6} q_{7,7} + 102 q_{6,7} q_{7,4} + 72 q_{6,7} q_{7,5} + 72 q_{6,7} q_{7,6} + 102 q_{0,4} + 72 q_{0,5} + 72 q_{0,6}
計算
objective = left_objective + right_objective
constarints = constarints_1 + constarints_2
model = objective/1000 + constarints
# モデルをソルバーに渡して求解し、結果を取得
result = solve(model, client)
# 制約条件を満たす解が得られなかった場合は、RuntimeError を出す。
if len(result) == 0:
raise RuntimeError("The given constraints are not satisfied")
values = result.best.values
q_values = gantt.evaluate(result.best.values)
print(f"{result.best.objective=}")
for index, value in enumerate(q_values):
print(value)
print("=========")
for n in notes:
print(n)
result.best.objective=3.864993950290613e-07
[1. 0. 0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0. 1. 0.]
[1. 0. 0. 0. 0. 0. 0. 1.]
=========
[1, 0, 0, 0]
[0, 1, 0, 0]
[0, 0, 1, 0]
[0, 0, 0, 1]
計算Ver2
以下のように、重み付をすると良いらしいが、今回は保留。
objective = left_objective**2 + right_objective**2
constarints = constarints_1 + constarints_2
coef = (102*total_notes)**2 * 2
model = objective/coef + constarints
結果
以下の結果となった。
これを足の動きに変換すると、左足はずっと固定して、右足だけを動かすのが最短距離となった。
[1. 0. 0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0. 1. 0.]
[1. 0. 0. 0. 0. 0. 0. 1.]
考察
考えうるパターンを自分の手で計算してみると、確かに上記の右足だけ動かすのが最短であることがわかった。
ので、計算としては正しいが、ゲーム中の動きが反映出来ていないという改善点を見つけた。
具体的には、DDRは流れてくる矢印を左足、右足、左足、右足、左足、、、という風に交互に踏む方がリズムに乗りやすく良いとされている。
また、片足を動かし続けるのは距離は短いかもしれないが、疲れないという目的にも反している。
そのため、今回定式化したような単純な移動距離を求めるだけでは不十分ということが分かった。
今後の展望
ゲーム内の動きを定式化に取り込み、よりゲームに近い動きを求めてみたいと思いました。
数理最適化がとても勉強になりましたが、定式化次第で良くも悪くもなるということも理解出来たので、今後もこういう勉強を続けていきたいと思いました。