Openposeの3D化に関する調査

OpenPoseの3D化(3次元姿勢推定)に関する論文調査を行った結果を記載します。

目次

1. OpenPose
2. 3Dデータセットを要しない手法
3. 3Dデータセットを要する手法
4. pose推定に関するその他の話題

OpenPose

CVPR2017で発表された姿勢推定の手法です[1]。
単眼のRGB画像から，複数人の姿勢推定を同時かつリアルタイムで行うことを可能にした最初の手法として注目されています(以下の動画のようなもの)。

OpenPoseについては既に解説記事もたくさん出てるので省きますが，以下のスライドがかなり詳細までまとめてくれてあるので，これを見れば十分だと思います。
https://www.slideshare.net/ShunsukeOno/realtime-multiperson-2d-pose-estimation-using-part-affinity-fields-78988208

ただし，OpenPoseはあくまで2D姿勢推定であり，関節点の2D座標を推定します。そのため，OpenPoseの2D出力を3D化する研究が多く行われています。今回はそれらOpenPoseの3D化に関する論文を調査して見つかった手法についてまとめを書いていきます。

3Dデータセットを要しない手法

まず3Dのposeデータがなくても可能な手法について，調査で見つかったものを紹介します。

マルチビュー

複数視点の2Dから3Dを復元・推定するという物体認識でも一般に採られている手法で，シンプルですが高い精度も得られる方法です。複数台のカメラ，もしくはステレオカメラのようなものが必要になるため，それが許容できる場面での活用が考えられます。
※ただしOpenPoseにあったスマホ写真でも適用可能という手軽さは失う

3次元人体姿勢推定を実現するためのOpenPoseの拡張[2]

OpenPoseの入力としてステレオカメラの映像を利用して，左右の映像から個別に人体姿勢を推定し，これらの視差情報をもとに重回帰式で3次元人体姿勢の推定を行う手法です。

具体的な手順としては，下図のようにステレオカメラの撮影領域において，水平方向や垂直方向，奥行き方向に複数の基準点を設け，それらの基準点の座標$P(x_i, y_i, z_i)$と左映像の座標$(xl_i, yl_i)$，右映像の座標$(xr_i, yr_i)$との関係を高次多項式

P=A \cdot F(xl_i, yl_i, xr_i, yr_i)+ \xi

で求める。𝐀は𝑚 × 𝑛の行列，𝛏は残差，𝐅は左映像の座標$(xl_i, yl_i)$と右映像の座標$(xr_i, yr_i)$から対応する基準点の3D座標$(x'_i, y'_i, z'_i)$を推定する関数である。$A$は次式より最小二乗法で求める。

argmin∑‖𝐀 \cdot 𝐅(𝑥𝑙, 𝑦𝑙, 𝑥𝑟, 𝑦𝑟) − 𝐏‖^2 

次に，OpenPoseで求めたステレオ映像の2D pose座標$(xL_i, yL_i)，(xR_i, yR_i)$と，上式で求めた𝐀を利用して，3D pose

𝐏𝐨𝐬𝐞＝𝐀 \cdot 𝐅(𝑥𝐿, 𝑦𝐿, 𝑥𝑅, 𝑦𝑅)

を求める。なお，ステレオ映像を取得するためのステレオカメラに対して事前にステレオキャリブレーションを実施するものとする。

ここではマルチビューによる3D化の一例を示しました。マルチビューベースで，トップカンファのものとしてはLearning Monocular 3D Human Pose Estimation from Multi-view Images[3]という論文があったので，また読んだらまとめたいと思います。

学習に3Dデータセットを用いない3D姿勢推定

ここでは学習時にも推定時にも3Dデータセットを必要とせず，2Dから3Dを推定するアプローチを紹介します。推定時にも単一2D poseのみで良いため，特別なカメラも必要としません。

Unsupervised Adversarial Learning of 3D Human Pose from 2D Joint Locations[4]

https://nico-opendata.jp/ja/casestudy/3dpose_gan/index.html#Martinez2017
上記ページで詳細が載っていますが，要約すると，2D poseからdepthを推定し，それを用いて任意の視点で2Dに投影したときのposeデータが，破綻のないものにならないように学習するといったものです。以下の図のような敵対的学習により実現しています。

Generatorによって推定された2D poseであるか，それとも2Dデータセットにもとも存在するposeであるかを識別するDiscriminatorを用い， そのDiscriminatorを騙すようにGeneratorを学習することで，Generatorが生成する2Dポーズが，破綻のないものになるといった仕組みです。

実験映像は以下のサイトで見られます。
http://www.nicovideo.jp/watch/1522667104

論文を見た限りやはり教師ありの手法には精度は及ばないようですが，仕組みは上手くできており，完全な教師なし学習でここまで推定出来ているので，面白いアプローチだと思います。

#3Dデータセットを要する手法
これは様々な研究がされており，ここでは，3D poseのライブラリからOpenposeが出力した2D poseに近いものを選出するというアプローチと，OpenPoseが出力した2D poseから3D poseの教師データを用いてニューラルネットで推定するというアプローチを紹介します。

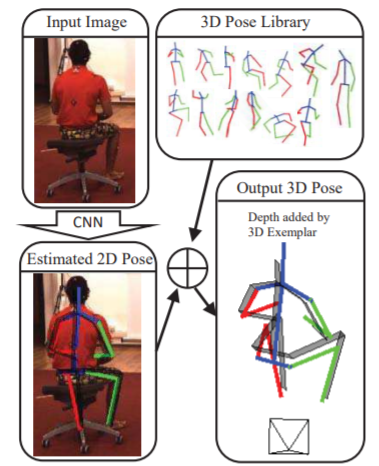
3D Human Pose Estimation = 2D Pose Estimation + Matching[5]

下図のように2D pose推定で得られたposeで3Dライブラリからマッチする3D poseを探索して得るというアプローチ。ここで，より入力poseに合うようにライブラリのposeを歪ませるという処理も行っています。

手法の詳細について説明していきます。
画像$I$，3D pose $X \in \mathbf{R}^{3N}$，2D pose $x \in \mathbf{R}^{2N}$，関節点の数$N$において，

p(X, x, I)=p(X|x) \cdot p(x|I) \cdot p(I)

をモデル化することを目指します。$p(x|I)$は2D pose推定のためのCNN，$p(X|x)$は提案手法による3D化モデルが対応し，この論文では，ノンパラメトリックな手法であるnearest-neighbor(最近傍法)を用いています。
ここで，ライブラリは特定のカメラ射影行列{$M_i$}と，対になる3D pose{$x_i$}を有することを前提としており，関連する2D poseが{$M_i(X_i)$}によって与えられます。この辺はカメラキャリブレーションの知識が必要になります。http://opencv.jp/opencv-2.1/cpp/camera_calibration_and_3d_reconstruction.html

再投影誤差に基づいて3D poseの分布を以下のように定義します。

P(X=X_i|x) ∝ e^{−\frac{1}{σ^2}||M_i(X_i)−x||^2}

このMAP推定値は，1-NNによって与えられます。

また，ライブラリの模範からの深度値に関しては単純にコピーし，以下で与えられるweak perspectiveモデルで2D pose推定からの値を歪ませてコピーすることにより，より入力の2D poseに一致度の高い推定結果$X^*$を得ています。

X_i^* = [sx \quad sy \quad Z_i], \quad where \ s = \frac{average(Z_i)}{f}

ここで，$f$はカメラの焦点距離($M_i$)の内部関数で与えられ，$average(Z_i)$は3D関節の平均深度です。

A simple yet effective baseline for 3d human pose estimation[6]

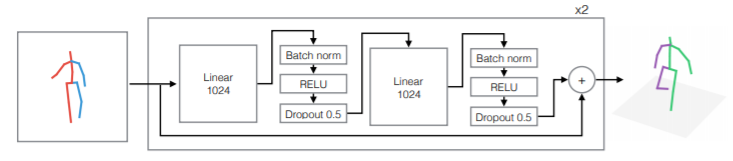
ニューラルネットにより単眼の2D pose情報から3D pose情報を回帰する手法です。画像ではなく関節の座標点の2D→3Dを学習するため，軽量なモデルで実現できます。その他にも，Residualコネクション，BN，ドロップアウト等を駆使して，なるべく軽量で高速に推論処理が出来るようにしています(学習パラメータ数は400万-500万程度)。

関節点の数$N$，データセットもしくはopenposeの出力の2D座標点$x_i \in \mathbf{R}^{2n}$，提案ネットワークの出力$y_i \in \mathbf{R}^{3n}$として，以下の誤差関数を最小化するように関数$f^*: \mathbf{R}^{2n} \rightarrow \mathbf{R}^{3n}$を求めます。

f^∗ = \min_f \frac{1}{N} \sum_{i=1}^N L (f(x_i) − y_i)

具体的には関数$f$はDeep NeuralNetで近似し，上図のようなネットワーク構造で，16個の2D関節座標点を入力し，16個の3D関節座標点を出力する。データセット「Human3.6M」(3D pose estimationのための主要なデータセット)は3D poseデータも含むため，これを教師データとして学習を行う。

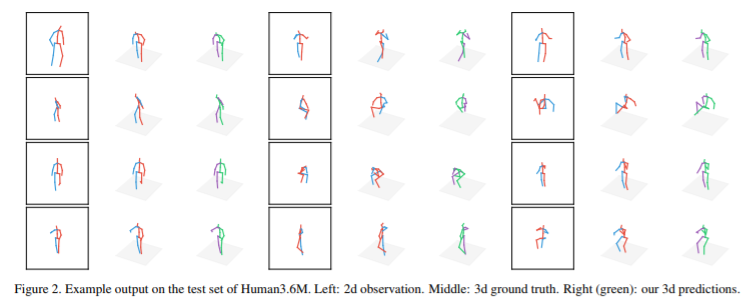
テストデータに対する推定結果は上図の通りで，左が入力の2D pose，中央が正解の3D pose，右が提案ネットワークによる推定結果です。シンプルな手法ですが，かなり精度良く推定出来ているように思われます。

こちらの手法は単眼RGB画像のみを必要とする手法であり，3D poseの教師データも十分用意されているため(今後さらにバリエーションも増えれば），このように教師ありの手法で3D化を行うのが最も良いのではないかと思われます。

補足

pose推定に関するその他の話題について紹介します。

教師ラベルの補正

姿勢推定用のデータセットでは，下図(a)のように，Limbが画像の外に出てしまい，アノテーションがされていない，つまり下図(b)のように適切な教師ラベルを生成できないようなデータが混在しています。その他アノテーション漏れなどもあり，このようなデータから生成した教師ラベルは，モデルの学習に悪影響を及ぼす懸念が考えられます(モデルが本来なら正しい位置のヒートマップ，PAFを出力しても，アノテーション漏れによりFalse Positive扱いになってしまう)。
そこで，下図(c)のように教師ラベルよりも学習済みモデルの出力の方が適切な事例が存在することに着目し，Knowledge Distillationを用いた教師ラベルの補正手法が提案されています。

実際，以下の図のように適切に補正されたデータが得られるため，これを教師データに使うことで，実際に精度向上が達成されています。

一般的に，子モデルの出力を$P_S$，教師モデル(学習済み)の出力を$P_T$，教師ラベルを$y_{GT}$，$E$を平均二乗誤差として，以下のように未補正のラベルと教師モデルの出力を教師とした二乗誤差の重み付き平均$E_{KD}$を誤差関数として用いて学習されます。

E_{KD}=(1-\lambda)E(P_S, y_{GT})+\lambda E(P_S, P_T)

ここで，$\lambda$はそれぞれの二乗誤差の混合比率を調整するパラメータです。$\lambda$を0以上に設定して精度改善が得られたという結果から，学習に影響があったことが分かり，「教師ラベルの補正」というアプローチも2D pose推定の精度向上において重要な要素であると言えます。

まとめ

本記事では，OpenPoseの3D拡張に関連した手法を紹介してきました。ここで紹介したもの以外にも様々な手法が提案されていますが，個人的には教師あり学習で推定する手法が精度・利便性(スマホカメラで可)の面で優れているのではないかと思われます。

ちなみにOpenposeの3D化はキャリブレーション済みの複数台カメラを設置して三角測量により3D化を行う手法を取っています。
https://github.com/CMU-Perceptual-Computing-Lab/openpose/blob/master/doc/modules/3d_reconstruction_module.md

本家(CMU)の続編にあたる論文(3D化，およびhand, faceの追加)については，CVPR2018で「Total Capture: A 3D Deformation Model for Tracking Faces, Hands, and Bodies」というタイトルで発表されています。

• Body：本家OpenPoseを使用
• Hand：論文「Hand Keypoint Detection in Single Images using Multiview Bootstrapping」の手法
• Face：論文「IntraFace」の手法

これらの論文についても，余裕があれば本家CMUの手法としてまとめたいと思います。

その他，個人的に面白そうなものとして，Point Cloudで手の姿勢推定を行う[8]という論文もありました(余裕があれば追加します)。まだまだ筆者の調査不足の面もあると思われるため，今後面白そうな手法が見つかったら追加していきたいと思います。

※なお，記事内の間違いの指摘等ありましたら，ぜひコメントお願い致します。

#参考文献
[1]Zhe Cao, et.al, Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields, CVPR2017
[2]大野祐汰ら, 3次元人体姿勢推定を実現するためのOpenPoseの拡張, エンタテインメントコンピューティングシンポジウム(EC2017), 2017/9
[3]Helge Rhodin, et.al, Learning Monocular 3D Human Pose Estimation from Multi-view Images, CVPR2018
[4]Yasunori Kudo, et.al, Unsupervised Adversarial Learning of 3D Human Pose from 2D Joint Locations, arXiv:1803.08244, 2018/3/22
[5]Ching-Hang Chen, et.al, 3D Human Pose Estimation = 2D Pose Estimation + Matching, CVPR2017
[6]Julieta Martinez, et.al, A simple yet effective baseline for 3d human pose estimation, ICCV2017
[7]加藤 直樹, 李 天琦, 西野 剛平, 内田 祐介, 複数人物姿勢推定におけるKnowledge Distillationを用いた教師ラベル補正手法の提案, 第21回 画像の認識・理解シンポジウム(MIRU2018)
[8]Liuhao Ge, et.al, Hand PointNet: 3D Hand Pose Estimation Using Point Sets, CVPR2018
※書式適当ですみません