最尤法 ～LogLogisticDistributionを例に～

#前置き：Log Logistic Distributionについて
log Logistic Distributionという確率分布があります。(以下loglogistic分布と略)

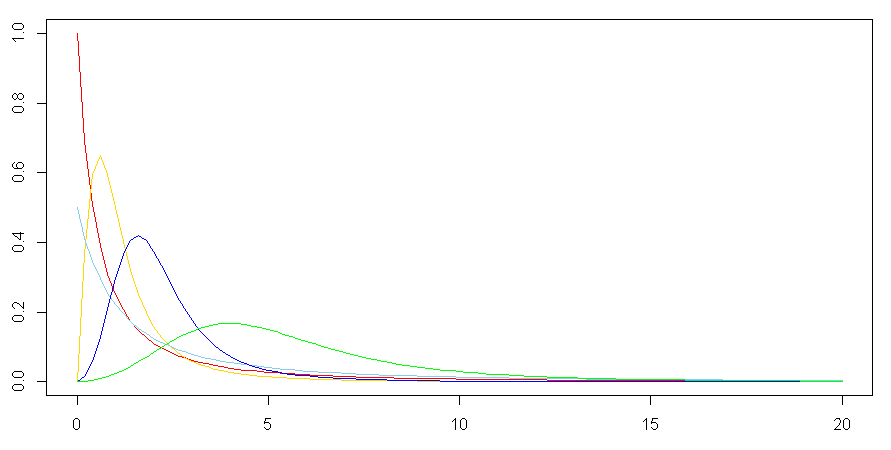
赤色：$\alpha$=1 , $\beta$=1
黄色：$\alpha$=2 , $\beta$=1
空色：$\alpha$=1 , $\beta$=2
青色：$\alpha$=3 , $\beta$=2
緑色：$\alpha$=3 , $\beta$=5

「非負の二つのパラメータ」$\alpha$ , $\beta$からなる上図のような裾の重い確率分布で、その確率密度関数を$f(x;\alpha,\beta)$とすると
$$
f(x;\alpha,\beta)=
\frac{\beta(\frac{x}{\alpha})^{\beta-1}}
{\alpha[1+(\frac{x}{\alpha})^{\beta}]^{2}}
$$

またn個の観測値がこのloglogistic分布から得られたものとして、その対数尤度をlとすると、
$$
l=n(log(\beta)-log(\alpha))+\sum_{i=1}^n [(\beta-1)log(\frac{x_i}{\alpha})-2\log(1+(\frac{x_i}{\alpha})^\beta)]
$$
が得られます。

#本題：riversデータとLoglogistic分布の最尤推定
Rに標準実装されているデータセットにriversというものがあります。
北米にある141の主要な河川の長さ(単位：mile)のデータで、density()で密度推定してみると下図のようになっています。
plot( density(rivers) )

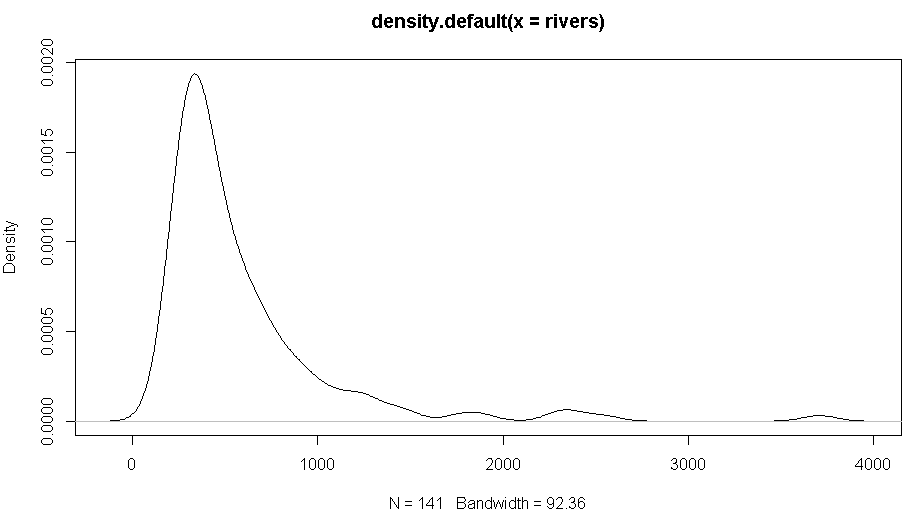
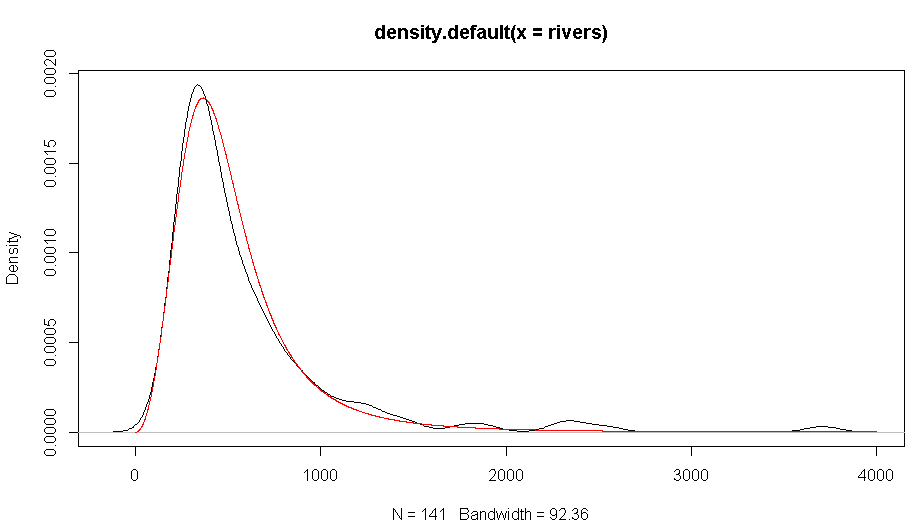
このriversデータに対してloglogistic分布を当てはめ最尤推定をしてみます。
但し重要な点が一つあります。
通常であればoptim関数を使って対数尤度を最大化すればそれでよいのですが、logligistic分布の場合はそうはいかない。
というのも、二つのパラメータα,βはともに非負であるという制約があるので単純にoptim関数で最適化するには不都合なわけです。
そこで非負制約下の最適化問題(不等式制約下の最適化問題)に対応できるconstrOptimの出番。

#対数尤度#
loglikelihood<- function(x){
    return(
      function(parameter){
       alpha <- parameter[1]
       beta <- parameter[2]
       n<-length(x)
     return( n*(log(beta)-log(alpha))+sum( (beta-1)*log(x/alpha)-2*log(1+(x/alpha)^beta) ) )
    }
  )
}

#制約条件：α>0,β>0に対応#
ui <- matrix(c(1, 0, 0, 1),ncol=2,nrow=2)
ci <- c(0, 0)

#制約付き最適化#
constrOptim(c(1, 1), loglikelihood(rivers), grad=NULL, ui=ui, ci=ci, control=list(fnscale=-1))

さて得られた推定結果を基に曲線を当てはめて見ましょう。

parameter<-constrOptim(c(1, 1), loglikelihood(rivers), grad=NULL, ui=ui, ci=ci, control=list(fnscale=-1))$par
x<-seq(0,4000,1)
plot( density(rivers) )
lines( dllogis(x,parameter[2],parameter[1]),col="red" )

※赤が最尤推定に基づくLogLogistic分布

まずまず良い結果が得られたのではないでしょうか。

#オマケ：loglogistic分布をstanに実装してみる
loglogistic分布をstanに実装してみます。
※rstan：Version 2.16.2

library(rstan)
y<-rivers
data<-list(y=y,N=length(y))

log_logistic_code <- "
functions{
 real log_logistic_lpdf(real y, real alpha, real beta){
  return( log(beta)+(beta-1)*log(y/alpha)-log(alpha)-2*log(1+(y/alpha)^beta) );
 }
}

data { 
  int<lower=0> N; 
  real y[N]; 
} 
parameters { 
  real<lower=0> alpha;
  real<lower=0> beta;
} 
model {
  for(t in 1:N){ 
   y[t] ~ log_logistic(alpha,beta); 
  }
} 
"
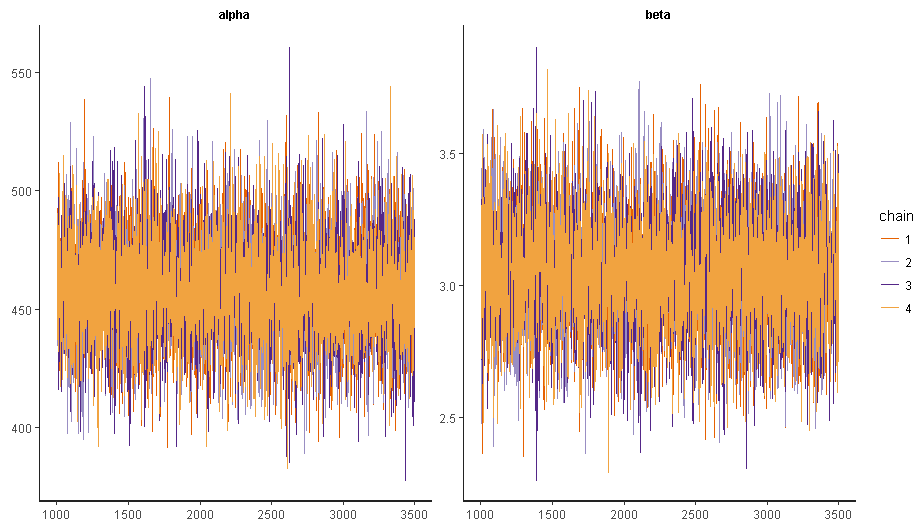
log_logistic<-stan(model_code=log_logistic_code,data=data,seed=3141592,chains=4,warmup=1000,iter=3500)
print(log_logistic)

最尤推定値とおおむね一致しますね。

#参照
・wikipedia：Log-logistic distribution
・Package 'eha' - CRAN.R-project.org