Pythonを用いて日経225を分析する

目標

2017年1月1日から2017年12月31日までの日経225の日時データを入手し、日次リターンの平均と分散及び、ドリフトとボラティリティを計算する。
その結果を用いて、ヒストグラムを描く。
#準備
株価の変動が幾何ブラウン運動に従うと考える。つまり株価は、
$$ \frac{dS_t}{S_t} = {\sigma}dW_t+\mu{dt} $$
に従う。これを離散化すると、
$$ \frac{{\Delta}S_t}{S_t} = {\sigma}{\Delta}W_t+\mu{{\Delta}t} $$
となる。ここで、$ \Delta{S_t}=S_{t+{\Delta}t}-S_t $とする。$\Delta{t}$は約1/250と以下で計算される。これは取引所が開いている日数がおよそ250日であることによるものであり、休日ににおける資産の価格形成は無視するとする。株価の日次リターンとは、$\frac{\Delta{S_t}}{S_t}$のことであり、推定される$\mu$と$\sigma$はこの平均と分散それぞれを$\Delta{t}$で割ったものである。

#分析
まず以下をimportする。

import numpy as np
import datetime
from scipy.stats import norm
import pandas_datareader.data as web
import matplotlib.pyplot as plt

pandas-datareaderで日経平均225を取得。dropnaで株価がNaNの部分を除く。

start = datetime.datetime(2017, 1, 1)
end   = datetime.datetime(2017, 12, 31)
ni225 = web.DataReader("NIKKEI225", "fred", start, end) 
ni225modi = ni225.dropna(how='all', axis=[0, 1])
nikkei225 = ni225modi.as_matrix()

株価の日次リターン、平均、分散等を計算する。

L = len(nikkei225)
#delta = 1/len(nikkei225)

S = np.zeros(L, dtype = float)
for i in range(0,L-1):
    S[i] = (nikkei225[i+1]-nikkei225[i])/nikkei225[i]
    
mu = S.mean()*L
sigma = np.sqrt(S.var()*L)
mean = S.mean()
var = S.var()

ドリフトとボラティリティはそれぞれ0.1566,　0.1150と推定された。

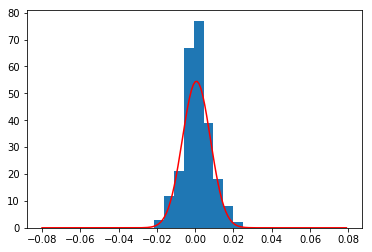
次に、ヒストグラムと正規分布のグラフを表示する。binsの値は9。

#スタージェスの公式を用いて`bins`を求める
HistBins = int(np.round(np.log2(L)+1))
count, bins_edges, patches = plt.hist(S, bins = HistBins)

X = np.arange(-0.08,0.08,0.001)
#確率密度関数に,平均mean、標準偏差var^(1/2)を代入
Y = norm.pdf(X,mean ,np.sqrt(var))
plt.plot(X,Y,color='r')
plt.show()

赤のグラフが日次リターンの平均と分散を用いた正規分布。青のグラフが日次リターンのヒストグラム。