自動車の燃費を予測してみた。【signate練習問題】その２

　こちらの記事をご覧いただきありがとうございます。
　↓の続きです。

　前回の簡単なまとめをしておきます。

• 燃費、シリンダー、排気量、馬力、重さの5つは密接な関係にある。多分、車の目的に応じて設計されるためだと思われる。
• 年を経るにつれて燃費が向上する。特に70年以降は低燃費化が進められていた背景がある。
• originはメーカーの国。originごと燃費の差はありそう。メーカーごとの燃費の差は微妙。

クラスタリングを使ってデータの性質を探る。

　ここから機械学習のモデルを使用した分析を行います。
　回帰予測の問題なので回帰モデルを…の前に、クラスタリングでデータの性質を探してみます。この目的は、先に行ったデータの可視化とおおよそ同じで、データの持つ性質がわかることで後の回帰分析に役立つ可能性があるからです。
※個人的には予測がどうこうよりデータの法則性みたいなものが知れる方が嬉しかったりします。

　モデルによってどういう分類がされるのか検証したかったので、様々なモデルを試します。

kmeans法

　クラスタリングでは基本的（だと個人的に思っている）なkmeans法から試します。
　と思ったところで、kmeans法だとカテゴリ変数を扱えないことに気が付きました。cylindersもoriginもint型で入っている（そうでなくてもlabel encodingでint型に変換できる）ので実行できなくはないですが、分析結果の解釈が出来なくなります。カテゴリ型を含めて分類できるkmeansの親戚みたいなモデルがあるらしいので、それを後ほど試します。先に、量的変数だけ残してkmeans法を試してみます。

前処理

欠損値処理

　モデルがうまく機能するように前処理します。
　まず、可視化の時点ではなかったことにしていたhorsepowerの?の埋め合わせをします。cylindersとmodel yearがmpgに大きく関係ありそうなことから、cylindersとmodel yearでgroupbyした後の平均値で埋めます。埋めた後に、データ型をfloatに変換します。

欠損値を埋める

mean_group_cy_ye = df_train_nn.groupby(['cylinders','model year']).mean()
df_train_cy_ye = copy.copy(df_train)
df_train_cy_ye.loc[df_train_cy_ye['horsepower']=='?','horsepower'] = df_train[df_train['horsepower']=='?'].apply(lambda x: mean_group_cy_ye.loc[x.cylinders,x.model_year]['horsepower'], axis=1)
df_train_cy_ye.horsepower = df_train_cy_ye.horsepower.astype(float)

埋めた場所の確認

df_train_cy_ye[df_train['horsepower']=='?'][['cylinders','model_year','horsepower']]

出力結果

　※出力結果がpythonのDataFrame出力と異なりますが、画像出力が楽な手段があったのでそれを使いました。画面をスクショしてトリミングして保存して…だと毎回そこそこ手間がかかっていたので、DataFrameを画像として出力する手段を探していたらありました。
　以下で関数として利用できます。

DataFrameを画像にする

# dfは出力したいDataFrame
# wは横幅、hは縦幅
# outputPathは出力先のパス

def TablePlot(df,w,h,outputPath):
    fig, ax = plt.subplots(figsize=(w,h))
    ax.axis('off')
    ax.table(
        df.values,
        colLabels = df.columns,
        loc = 'center',
        bbox=[0,0,1,1]
    )
    plt.savefig(outputPath)
    plt.show()

不要な列を削除

　kmeansで利用できる量的変数のみ残るように、不要な列を削除します。model yearのような重要な変数も落としてしまうので、このkmeansにどれだけの意味があるか怪しくなってきました。

不要な列を削除

feature_names = ['mpg', 'displacement', 'horsepower', 'weight','acceleration']
df_train_km = df_train_cy_ye[feature_names]

標準化

　kmeansが適用できるように標準化します。

標準化

from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
km_train_ss = ss.fit_transform(df_train_km)

　標準化をして、前処理は完了です。

モデルで学習

　kmeansでグループ分けをしてみます。グループの数はとりあえず3つにして後で数を変えて試します。

kmeans法

from sklearn.cluster import KMeans
# クラスタ分け
KM = KMeans(n_clusters=3, random_state=0)
KM.fit(km_train_ss)
cluster = KM.predict(km_train_ss)
# dfにクラスタを付け足す
df_train_km3 = copy.copy(df_train_cy_ye)
df_train_km3['cluster'] = cluster
# 散布図を出力
sns.relplot(data=df_train_km3, x='displacement', y='mpg', hue='cluster')
plt.show()

displacement,mpgとクラスター分け

　クラスターの違いで色分けをしています。これを見ると、displacementの大きさで3つに分けているような印象がありますね。
　ヒストグラムで見ると、よりdisplacementの大きさで分けた感が感じられます。

displacementのヒストグラムとクラスター分け

　displacementのところをhorsepowerやweightで置き換えてもおおよそ同じ結果が得られました。似たようなデータなんだなーと改めて感じます。

　たしかシリンダーも同じような傾向になるよな？と思ってクラスターとcylindersの関係を確認します。

積み上げ棒グラフ

crosstable = pd.crosstab(df_train_km3.cylinders, df_train_km3.cluster, normalize='index')
crosstable.plot.bar(stacked=True)
plt.legend(bbox_to_anchor=(1,1))
plt.show()

cylindersとクラスター

　おおよそシリンダーとクラスター分けが同じになるようですね。kmeansにシリンダーの情報を入れていないので、データの特徴は大雑把にcylindersで説明できそうです。

　他にも見てみましたが、可視化で得た情報以上に有益なデータは得られませんでしたので、割愛します。

　クラスタ数を5にして試しました。同じような感じで5層に分かれるんかな…？

displacement.mpgとクラスター5

　うーん、kmeans法がうまく行っていない印象がありますね。5分割もする必要ないんでしょうか？
　と思っていたところで、クラスタ数を考えるための指標になるものを作れることを思い出したのでやってみます。エルボー図というものを出力します。

エルボー図の作成

inertia = []
for i in range(2,22):
    KM = KMeans(n_clusters=i, random_state=0)
    KM.fit(km_train_ss)
    inertia.append(KM.inertia_)
    
plt.plot(inertia)
plt.savefig('./img/kmeans_elbow.png')
plt.show()

エルボー図

　(;^ω^)
　真面目にこんな顔してたと思います。
　エルボー図というのをザックリ説明すると、曲線がカクっと折れているところがクラスタ数としてちょうどよいことを表してくれます。このグラフは滑らかに曲がっているので、どこがちょうどよいのかわからないってことですね。
　言われてみれば確かに、量的変数は(acceleration以外)だいたい同じような性質で直線でも表せそうな変化をしていたので、わからんでもないような気がしてきました。
　たぶん、このデータセットにkmeansは適してないのでしょう。

カテゴリ変数が使える教師なし分類

　kmeansにカテゴリ変数が使えないことに気が付いてから、教師なし分類でカテゴリ変数を利用できる方法を調べました。ネットで紹介されていた手法があったので、それを試します。
　紹介元は↓をご覧ください。

　まずデータサンプルを Gower距離 行列に変換します。Gower距離行列とはカテゴリ変数を含めてデータ点間の距離を計算できるものだそうです。話が長くなるので説明は割愛します。私は↓を見て確認したので、良ければそちらもご覧ください。

　Gower距離行列に変換した後は、ward法などのクラスタリング手法で分類してもらうって感じです。

Gower距離行列に変換

前処理

　うまくGower距離行列に変換できるように前処理をします。量的変数は標準化、質的変数はカテゴリ型に変換します。（カテゴリ型は数字でもカテゴリとして扱うらしいです。）

Gower距離変換の前処理

# 量的変数を標準化
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()

df_train_ss = copy.copy(df_train_cy_ye)
quantity_features = ['mpg', 'displacement', 'horsepower', 'weight','acceleration']
df_train_ss[quantity_features] = ss.fit_transform(df_train_ss[quantity_features])
df_train_ss

# 質的変数をカテゴリ型に変換
quality_features = ['cylinders', 'model_year', 'origin', 'car_name']
df_train_ss[quality_features] = df_train_ss[quality_features].astype('category')

Gower距離に変換

　前処理が済んだので、Gower距離行列に変換します。

# Gower距離行列に変換
import gower

df_train_gw = copy.copy(df_train_ss)
df_train_gw .drop(['id','car_name'],axis=1)
df_train_gw = gower.gower_matrix(df_train_gw)

Category型は不可

　カテゴリ型のデータは扱えないらしいです。Gower距離ってカテゴリを扱うためのものではなかったのか…？
　カテゴリ変数をobject型に変換してからGower距離に変換します。

カテゴリ変数はobject

# 質的変数をobject型に変換
quality_features = ['cylinders', 'model_year', 'origin', 'car_name']
df_train_ss[quality_features] = df_train_ss[quality_features].astype('object')

# Gower距離行列に変換
import gower

df_train_gw = copy.copy(df_train_ss)
df_train_gw .drop(['id','car_name'],axis=1)
df_train_gw = gower.gower_matrix(df_train_gw)

変換に成功

　いかにも距離行列っぽくなりましたね。これを使ってクラスタリングを試します。

Gower距離行列をkmeansする

　距離行列をそのままKMeansモデルにぶち込みます。

Gowerでkmeans

# Gower距離行列でkmeans
from sklearn.cluster import KMeans
KM = KMeans(n_clusters=3,random_state=0)
KM.fit(df_train_gw)
cluster = KM.predict(df_train_gw)
df_train_cy_ye['cluster'] = cluster

　これも散布図を出力して性質を確認します。

displacement,mpgとcluster

　…見覚えがありますね。量的変数だけでkmeansしたときとかなり似ています。画像の貼り間違えを3回確認しました。
　確認したら、displacementが低くてmpgが高いデータの数が増えて、中間のデータの数が減っていました。

　どういう性質を持っているかよりわかりやすい可視化があるので、それを貼ります。

cylindersとcluster

　クラスタ分けはほぼほぼシリンダーの分類と同等らしいですね。車の性質はシリンダを見ればだいたいわかる、くらい言えるかもしれません。

　もう一つ、model_yearとclusterの関係を載せます。

model_yearとcluster

　clusterが1のデータは80年以降に存在しないようですね。clusterが1のデータはほぼcylinderが8のデータで、燃費が低い代わりに重くてパワーが高い車です。時代が流れてパワーを出す必要がなくなったということでしょうか。需要の移り変わりを感じますね。

　他の可視化したものも確認しましたが、やはりというべきか量的変数だけでkmeansしたパターンとあまり変わらなかったので割愛します。

エルボー図

　ちょうどよいクラスタ数を確認するためにエルボー図を出力します。

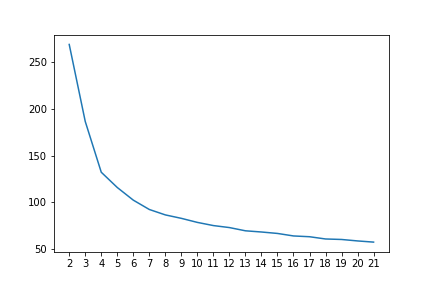
　割となめらかなのはそうだろうなーと思っていましたが、4のところだけ若干折れている感が見て取れます。クラスタ数4がちょうどよさそうです。

クラスタ数4でkmeans

　早速図を見てみましょう。見やすい配色に変えられる手法を発見したので、色が変わっています。

displacement,mpgとcluster

　クラスタ数3の時にdisplacementが低かったグループが2つに分かれた印象があります。ただ、その別れ方はdisplacementやmpgとはあまり関係なさそうです。
　他の図も確認します。

horsepower,mpgとcluster

weight,mpgとcluster

　horsepowerやweightはdisplacementと同じような傾向になりますね。これらもあまり関係なさそうです。

acceleration,mpgとcluster

　あまり注目してこなかったaccerelationですが、ここでもあまり関係はなさそうです。

cylindersとcluster

　cylindersが4のデータにしか新しいクラスタはいないようです。燃費の良いグループが分かれていたので、cylindersが4しかいないのもわかります。

model_yearとcluster

　新しいクラスタは71年から少しづつ存在していて、82年にかなり数を増やしたみたいです。しかしこれだけだと年代と関係が深いとは言いにくい気がします。

originとcluster

　新しいクラスタが何なのかこれでよくわかりますね。cylindersが4でかつoriginが1なら新しいクラスタに分類されているのでしょう。言い換えれば、パワーが控え目な代わりに燃費が良く、かつアメリカ産の車ということです。なんでアメリカだけ切り分けたのか？という疑問が浮かびましたが、アメリカは燃費の良い悪いの幅が広いからじゃないでしょうか。多分。
　それと、アメリカは82年（81?）に燃費の良い車が多く生産されたようなことも感じます。時代の流れですね。

cylindersとoriginで切り分け始めたので、クラスタ数を増やしたら日本やヨーロッパも分かれるのか？と思ってクラスタ数を増やして試しました。

originと5つのcluster

　クラスタ数4つの時と比較して、originの2と3が色分けされたようです。想定通り、日本とヨーロッパを区別してくれました。

　…ところで、mpgに関係なくoriginで区別するならmpgの予測にあまり関係ないのでは？と思い始めてしまったので、kmeansはこの辺にしておきます。

次回に続きます。

　今回はクラスタリング全般を載せて次回から回帰モデルで予測しようと思っていましたが、kmeansだけで結構長くなってしまったのでここまでにします。次こそクラスタリングを終わりにします。
　ここまでご覧いただいた皆様、ありがとうございました。

　→次回が完成しました。ぜひこちらもご覧ください。