自動車の燃費を予測してみた。【signate練習問題】その１

pythonを使って自動車の燃費を予測してみました。

　こちらの記事をご覧いただきありがとうございます。

　この度は、機械学習を勉強し始めておよそ3か月の私が、勉強したことの実践として、signateにある自動車の燃費予測を機械学習を用いて行ってみました。
　記事を書く目的は私自身のアウトプットですが、ご覧いただいた皆様にも何か学びがあれば幸いです。

データの確認

　使用するデータは以下の変数を持ちます。

• cylinders : 使用されているシリンダーの種類
• displacement : 排気量
• weight : 車の重量
• horsepower : 馬力
• acceralation : 加速度
• model year : 年式
• origin : 起源
• car name : 車名
• mpg : 燃費（mile per gallon）

　mpgが目的変数になります。それ以外の8つの変数を用いて、mpgの値を予測します。
　データサンプル数は199です。

まずはサンプルデータについて知る

　最初にサンプルデータの各変数にどんな値が入っているか調べました。

• cylinders : 3~8のint。3と5はサンプル1個のみ。7はない。
• displacement : 71~454のfloat。平均は約183。
• weight : 1613~5140のfloat。平均は約2883。
• horsepower : object。中身は小数の数字データがほとんどだが、一部?が入っている。おそらく欠損値。
• acceralation : 8~23のfloat。平均は
• model year : 70~82のint。70とは1970を表すものと思われる。
• origin : 1~3のint。
• car name : object。アルファベットで車名が表記されている。toyota~とか知っている文字列もあった。

この時点でいくらか思うことが出てきました。

• cylindersとorigin はカテゴリの違いを整数で表しているっぽい(label encoding)
• 速さと重さの関係って高校で習った気がする（運動エネルギー？）
• 車の時代背景が分かればmodel yearも役に立てやすそう
• originがカテゴリだとして何を表しているのか？
• 車名にメーカーが乗っているのでうまく取り出せば役に立つかも

ドメイン知識を調べる

　変数の中身を見て、数字の意味をよく理解できたほうが良いと感じたので、車について調べてみました。

• シリンダーとはエンジンの重要なパーツのこと。cylindersはそのパーツの種類を表してそうなことを感じた。
• 馬力とはエンジンの出せる力の大きさ（意訳なので語弊がありそう）。重い車ほど強そう。
• 1970年代は車からの排気ガスによる大気汚染があり、対策が進められていた。また1973年にはオイルショックがありガソリン価格が急騰、低燃費化がすすめられた。時代に沿って車の技術進歩があるのはよくある発想だとして、時代背景からしても70～82の間に大きな性能の向上がありそう。
• $ \vec p = m \vec v$ という、運動量と質量、速さの関係式がある。もしくは、$ E = \frac{1}{2}mv $という、運動エネルギーと質量、速さの関係式がある。車の燃費がどちらと関係が深いのかはよくわからなかった（詳しく調べればわかりそうではある）。

　ほかにも調べたことはありますが、変数名から察せられたこととおおよそ同じだったので割愛します（高校物理をまあまあ真面目に勉強しておいてよかった）。

データを可視化する

　基本的な可視化手段を使って特徴量やそれらの関係性について確認しました。先に調べたドメイン知識の確認のほか、後のモデル分析にも役に立つはずです。

　可視化する前に、horsepowerの欠損値への対応をします。とりあえず小数値として扱えるように、?の列を取り除いた後にfloat型に変換します。

?を取り除く

import copy
df_train_nn = copy.copy(df_train.query('horsepower != "?"'))
df_train_nn['horsepower'] = df_train_nn['horsepower'].astype(float)

変数の相関を確認する

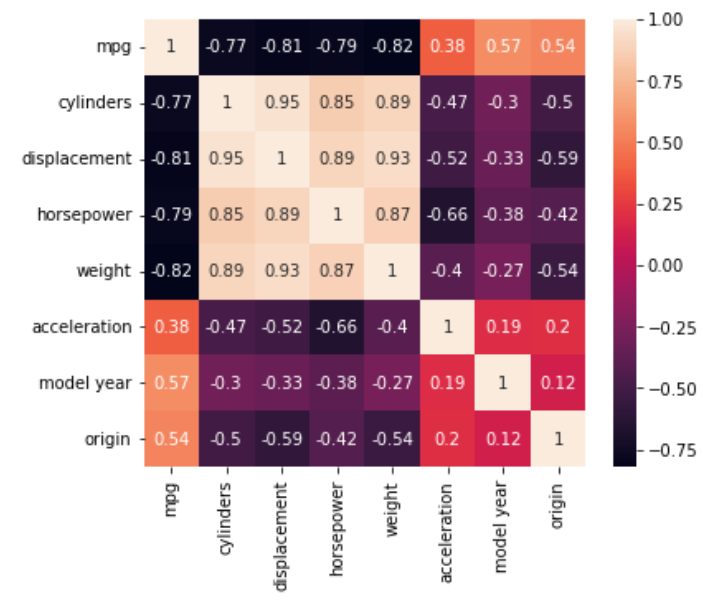
まずは各変数の相関を確認します。

相関のヒートマップ

import seaborn as sns

plt.figure(figsize=(6,5))
sns.heatmap(df_train_nn.corr(),annot=True)
plt.show()

　出力結果

cylinders,displacement,horsepower,weightの4つは正の相関が高く、またそれらはmpgと強めの負の相関を持っているようです。最悪説明変数がweightだけでもそこそこ再現できそうですね。
　また使用するモデルによっては多重共線性(変数同士の相関が高いと起こる問題)を考慮する必要があります。
　model yearやoriginもmpgそれなりの相関があります。

　このあたりで、cylinders,displacement,horsepower,weightとmpgの5つの変数の関連性が高いことから、一つの仮説を考え始めました。その仮説が、「車の使用目的に合わせて設計するなら5つの変数は似たような値になりそう」ということです。
　例えば、長距離運送用のトラックを作ることを考えたときに、大量の荷物を運べるように車体を大きくして必然的に重くなります。同時に、重い荷物をそれなりの速さで運べるようにするために馬力を高める必要があります。高い馬力を得るためには高出力のエンジン(シリンダー)を使う必要もあります。重いものを軽いものを運ぶ時と同じ速さで運ぶなら、重い分だけ多くの燃料を消費する(燃費が悪くなる)のも自然な考えだと思います。そして、燃料の消費量に伴って排気量も多くなる、と想定できます。
　つまり、先の5変数は車両の使用目的によっておおよそ決定する ものと考えられます。もちろん他の要素もいろいろかかわってくると思いますが、この5変数はかなり関係性が高そうです。

変数の特徴や変数ごとの関係を調べる

　変数ごとのヒストグラムや散布図も確認します。あらゆるパターンを乗せると数が多いので、私が注目したものを取り上げます。

相関の高い変数同士の関係は？

　まず確認したかった点が、相関の高い変数同士の関係性。相関が高いんだから右肩上がりか右肩下がりになるだろうって思わなくもないですが、それを確認しておくのも大事なことだと思います。

散布図の作成

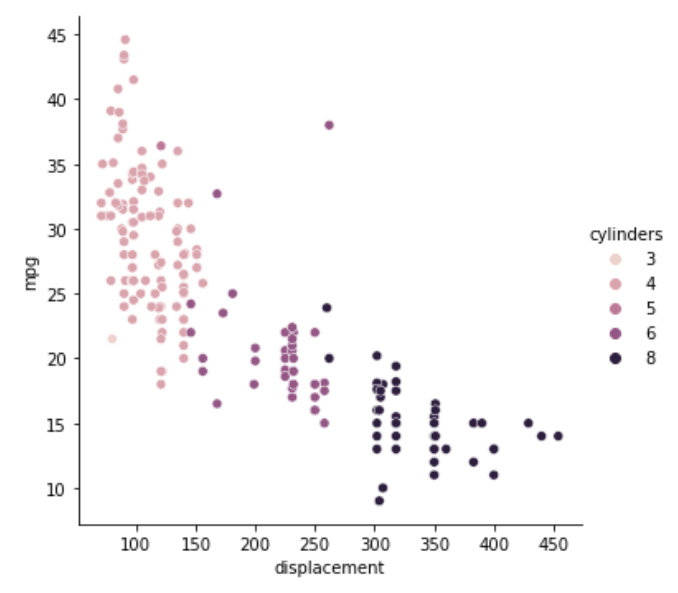
sns.relplot(data=df_train_nn,x='displacement',y='mpg', hue='cylinders')
plt.show()

mpg、displacement、cylinderの関係性

　これを見ると、displacementとmpgに強い負の相関があるのも納得します。cylindersによって色分けしていますが、シリンダー8は排気量が多く燃費が悪い、シリンダー4は排気量が少なく燃費が良い、シリンダー6はその中間、という傾向が確認できます。

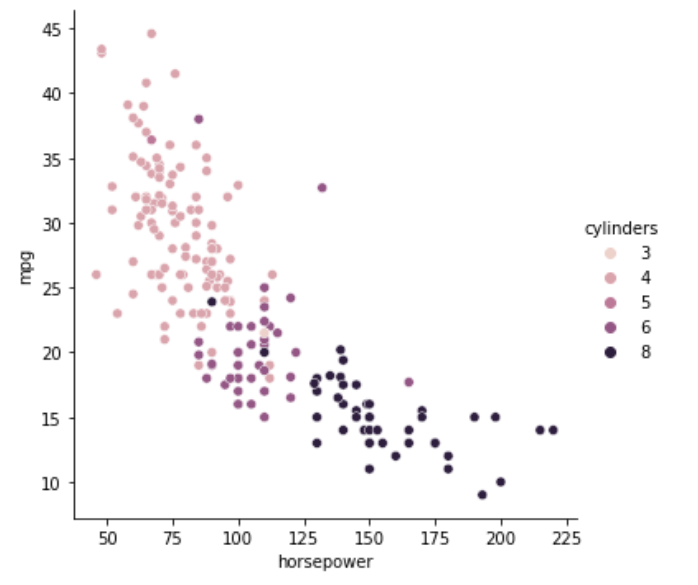
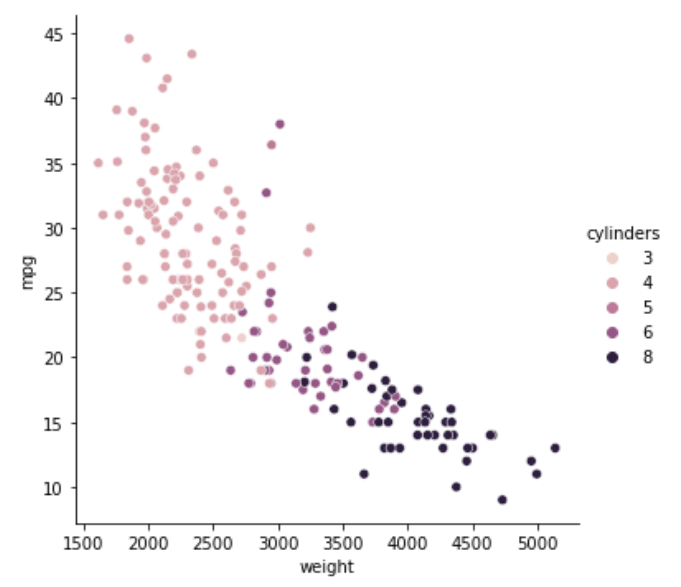
　同じような散布図を載せます。

mpg、horsepower、cylinderの関係性

mpg、weight、cylinderの関係性

　これを見ると、horsepowerやweightにもdisplacementと同様の傾向が見られます。このことから、さっき考えていた仮説「車の使用目的に合わせて設計するなら5つの変数は似たような値になりそう」も割と確信を持てそうな気がしています。
　シリンダー8は重い、排気多い、馬力高い、の特徴があり、トラックとかの長距離運送とか、もしくは悪路を走るためにパワーが欲しいとか、そんな可能性を感じます。
　シリンダー4は軽い、排気少ない、馬力低い、の特徴があり、整備された道路を走るならこんなもんかなーとか思ったりしました。

model year によって性能はどの程度変わるのか？

　70~82年代に低燃費化が進んだことを先に述べましたが、実際にどの程度のものなのか確認できる範囲で見てみました。

model year, mpg, cylinders の関係性

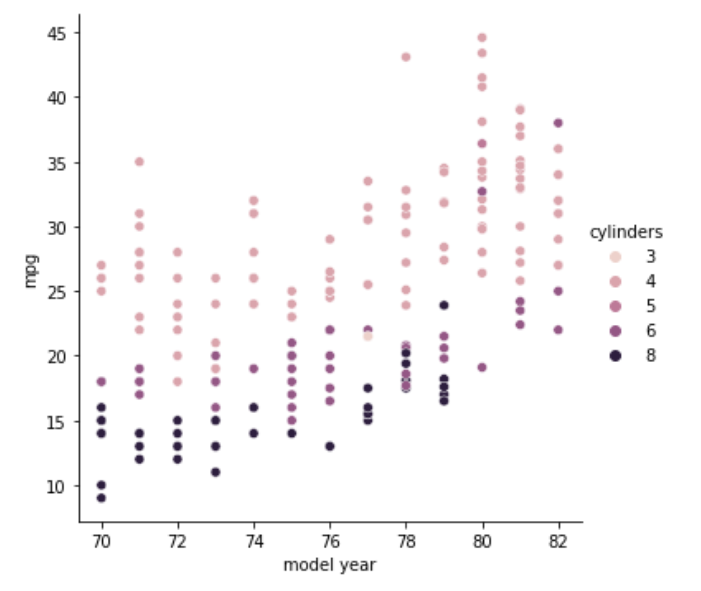
　これを見ると確かに、全体的に右肩上がりになっているので、時代が進むにつれて燃費が向上しているような印象がありますね。
　cylindersとの関係性も見れるように、cylindersの違いで色分けをしています。シリンダー4が白寄り、シリンダー8が黒寄りの色付けがされています。
　シリンダー8（黒）は80年以降あまり使われなくなっているようです。時代の変化とともに燃費の悪いものは使われなくなったみたいですね。交通網が整備されたからか、高い馬力が必要な場面がほとんどなくなった、というのが私の予想です。

　箱ひげ図も描いてみました。多分こっちのほうがわかりやすいような気がします。

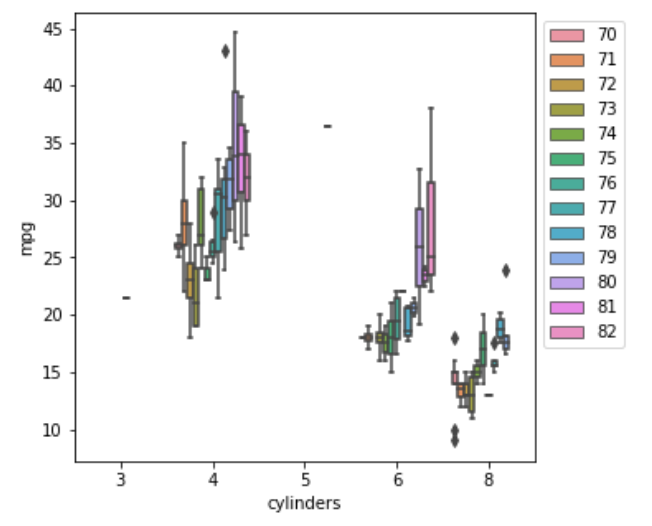
　特にシリンダー6は80年以降かなり燃費が向上しているようですね。シリンダー8は80年以降ほとんど使われなくなったこともわかります。

　他の散布図も見てみましょう。

model year, mpg, displacement の関係性

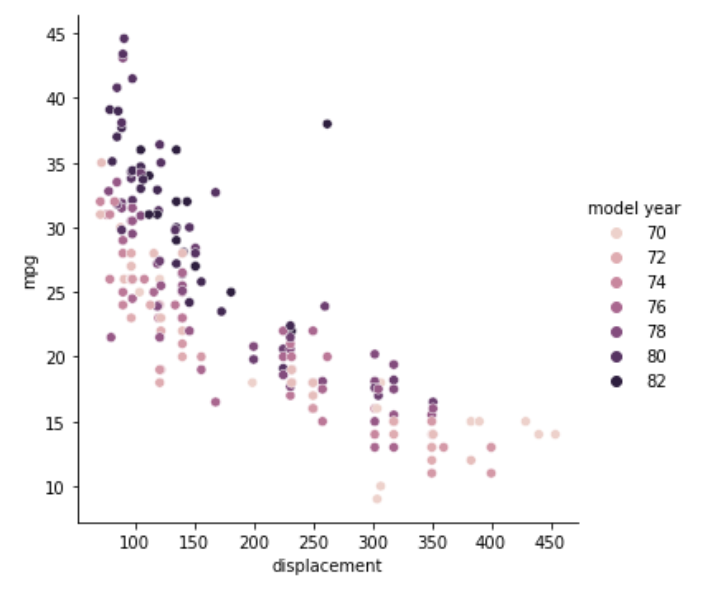
model year, mpg, horsepower の関係性

model year, mpg, weight の関係性

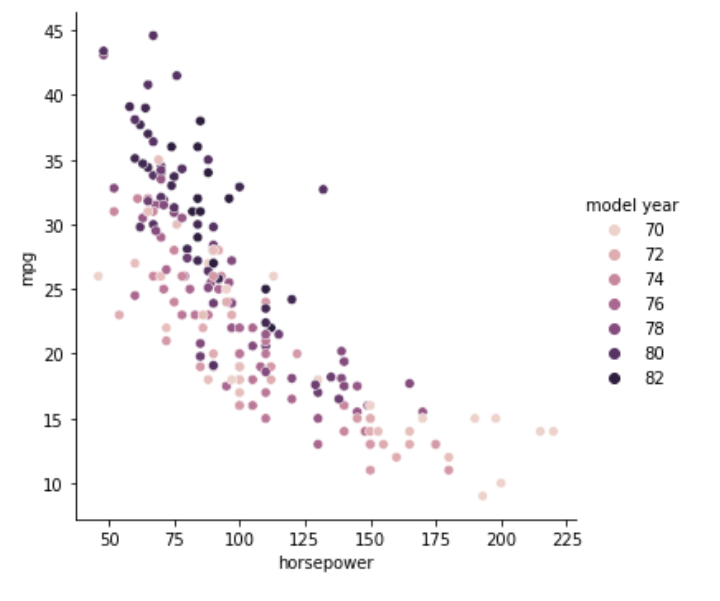
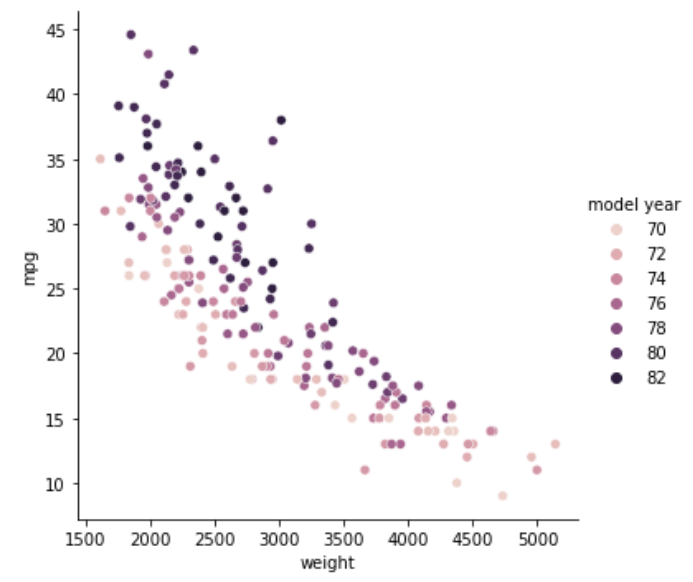
　今度はmodel yearによって色分けをしています。70年が白寄りで、時代が進むにつれて黒くなっていき、82年が黒になっています。
　displacementとhorsepowerとweightの3つはいずれも同じような散らばり方をしていますが、model yearを含めても同じ傾向になるようですね。白い点の古い車は下に集まっていて、黒い点の新しい車が上に集まっています。また、黒い点が左側に集まっていることから、時代が進んで重い、排気多い、馬力高い、の車があまり作られなくなったようです。低燃費化が進んでいるのは間違いなさそうですが、さらに時代の流れでそもそも馬力の高い車が必要なくなったと考えられます。

origin とは何者なのか

　originという変数名と1～3という中身だけではイマイチ何を表しているのかよくわからなかったので、これも可視化によって何か情報が得られないかとヒストグラムや散布図を作成しましたが、それでもイマイチよくわかりませんでした。
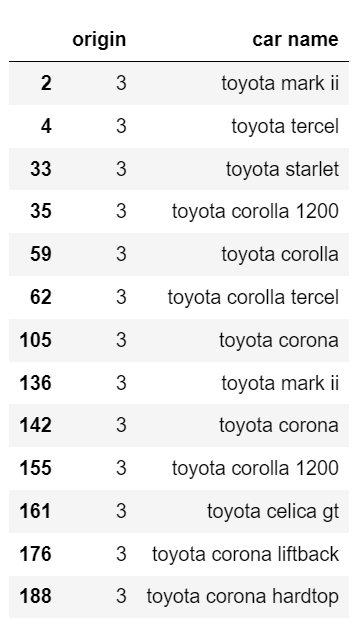
　このoriginが何者か気づいたのは、car nameを眺めていた友人でした。car nameにtoyotaの文字列が含まれているのは、originが3のデータだけという発見をしてくれました。実際に確認した結果が以下です。

'toyota'を含むデータを表示

df_train[df_train['car name'].str.contains('toyota')]

toyotaとorigin

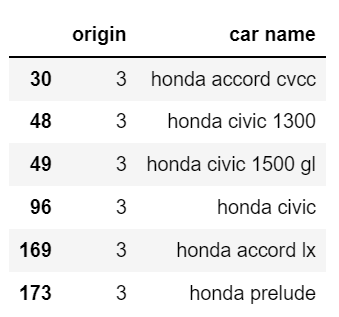
　確かに、toyotaを持つデータは全てoriginが3ですね。同じように、car nameにhondaを含むデータはどうだろうかと思って確認しました。

hondaとorigin

　こちらも全てoriginが3でした。この結果を見て、originは車のメーカーを表しているのでは？という仮説が生まれたので、検証します。
　car nameの文字列のうち、最初の1単語はメーカーを表す単語っぽいので、まずはそこだけを取り出すことを考えました。うまく取り出せたので、それをmaker変数として用意します。各メーカーがどのくらいあるのかを確認しました。

メーカーを取り出す

# 単語を空白で切り分けて、最初の単語を取り出してmaker変数とする
df_train_mk = copy.copy(df_train)
for id, name in enumerate(df_train_mk.loc[:,'car name'].str.split()):
    df_train_mk.loc[id,'maker'] = name[0]
# 各メーカーがどのくらいあるのか確認
df_train_mk.sort_values('maker').groupby('origin')['maker'].value_counts(sort=False)

メーカーごとのデータ数

　メーカー名を検索してどこの国か確認しましたが、originが1のメーカーはアメリカで、2はヨーロッパ、3は日本で間違いなさそうです。

　メーカーごとに燃費の違いがあるか確認してみました。

メーカーと燃費の確認

sns.boxplot(data=df_train_mk, x='origin', y='mpg', hue='maker')
plt.legend().remove()
plt.show()

makerごとの箱ひげ図

　originが2ならメーカーごとに燃費の差があると言ってもよさそうですね。ヨーロッパの地域差によるものでしょうか？　対して、originが1と3だとメーカーによる差があるとは言いにくそうです。そもそも母数が少ないメーカーもあるので、モデルに学習させるときにメーカー変数はあまり活躍しないような気がします…。

モデルによる予測は次の記事にします

　変数について個人的に気になったことはだいたい調べ終わったので、いよいよモデルで回帰予測…にしようと思いましたが、記事がかなり長くなりそうなのでここで区切ります。
　ここまでご覧いただいた皆様、ありがとうございました。

　次回の記事はこちらです。

signate の問題はこちらから

※練習問題に関する内容の公開は問題ないっぽいですが、何か問題があれば記事ごと削除します。