こちらの記事をご覧いただきありがとうございます。
↓の続きです。
前回の簡単なまとめをしておきます。
- ward法でクラスタリングをした
- ward法とkmeans法でだいたい同じ結果になった
- ward法のほうが
cylindersとoriginをよりきれいに再現した
クラスタリングの手法でkmeans法とward法（デンドログラム）を試しました。他にもクラスタリング手法はありますが(最近傍法とか)、今回は次元削減との組み合わせの手法を試します。
次元削減
次元削減って何？と思う人もいると思うので、一応簡単に説明しておきます。雑に言えば、元のデータが持っている情報をなるべく減らさずに別の形へと書き換えて、情報量の少ない変数をなかったことにします。
…テキストで伝えてもいまいち伝わらないと思うので、次の主成分分析を試すときに意識的に補足説明を増やします。
私が次元削減をするときに↓を参考にしたのでぜひご覧ください。
主成分分析
たぶん次元削減で一番基本的（だと個人的に思っている）な主成分分析から試します。
前処理
主成分分析でもカテゴリ変数をそのまま使えないので、Gower距離行列に変換します。量的変数だけの場合は標準化が必要です。
モデルで学習
（次元削減のモデル適用って学習と呼んでよいのでしょうか？）
Gower距離行列に変換したデータに主成分分析を適用してデータを変換します。
# 主成分分析で変換
pca = PCA()
pca.fit(df_train_gw)
df_train_pca = pca.transform(df_train_gw)
print(df_train_pca)
print(df_train_pca.shape)
変換前
変換後
主成分分析による変換が出来ました。
先にも書きましたが、主成分分析ではデータの情報量をなるべく減らさずに別の形に書き換えます。行列の形の変化もわかりやすいようにshapeもつけておきました。どちらも199×199ですね。データの形状の変化はありません。中身だけ変わりました。
この変換の何がうれしいかと言われれば、情報量が一部の変数に凝縮されることです。一番若い(?)変数（コードで書くならdf_train_pca[0]）に最も多くの情報を残し、若い順で情報量が多く残ります。最後の方の変数(df_train_pca[198])はカスみたいな情報量しか残っていません（たぶん）。
その説明として、主成分分析で変換した後の各変数の分散のグラフを載せます。
# 主成分分析変換後の各変数の分散
var = pd.DataFrame(df_train_pca).var()
plt.plot(np.arange(0,199), var)
plt.show()
横が変数の若い順、縦が分散
199個ある変数のうち、それなりに大きい分散を持つ変数はわずかしかありません。
主成分分析では、分散の大きさを持っている情報量の多さととらえています。多くの情報が最初の数個の変数に凝縮されているのがなんとなくでも感じられていればありがたいです。
さてもう一つ、主成分分析の各変数が持つ情報量を示すものとして、pca.explained_variance_ratio_があります。そのまま和訳すると「説明された分散比」らしいです。各変数が持っている情報量の割合を示してくれます。
そのまま表示するとこうなります。
# 各変数の情報量の割合
print(pca.explained_variance_ratio_)
変数の情報量の割合
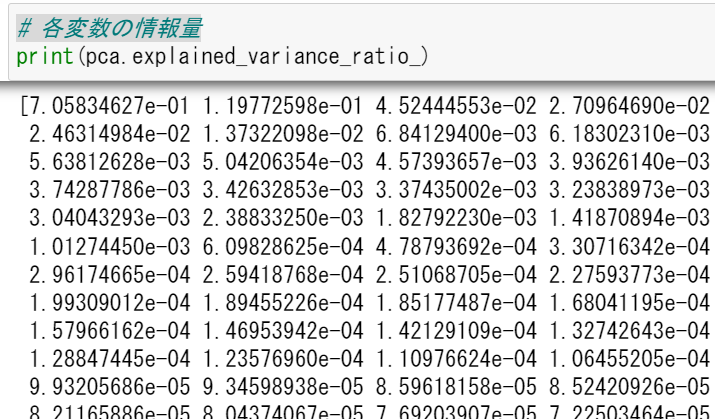
最初の 7.05834627e-01 ≒ 0.706 が、一番若い変数の情報量の割合を示しています。つまり、最初の一つの変数だけでおよそ70%の情報を持っていることを表しています。
これを累積和にするとこうなります。
# 累積和
explained_variance = np.cumsum(pca.explained_variance_ratio_)
plt.plot(np.arange(0,199), explained_variance)
plt.show()
情報量割合の累積和
さっきの情報量割合を累積和にしています。25の目盛のあたりで1.00近い数値になっていますが、これはつまり変数を25個残せばほぼ100％の情報が残ることを表しています。90％くらいでいいなら変数10個もいりません。
主成分分析の変数が持つ意味を調べる
主成分分析によってどう変わったのかを確認します。確認しやすいように、変数を2つに絞ってグラフ上にプロットします。もちろん、情報量が多い若い変数2つを残します。
plt.figure(figsize=(8,8))
plt.scatter(df_train_pca[:,0],df_train_pca[:,1])
plt.show()
主成分分析後の散布図
なんか2次曲線っぽさを感じますね。この散らばりの意味を確認するために、色付けして出力します。 mpgの値の大きさに応じて色のグラデーションを付けます。
グラデーションの付け方は以下を参考にしました。ぜひご覧ください。
先に色の説明をしておくと、黒が小さく、黄色が大きい、赤が中間です。以下の図のようになります。
import matplotlib.cm as cm
x =np.linspace(0,2*np.pi,100)
for i in range(30):
plt.plot(x,i*np.sin(x),color=cm.hot(i/30.0))
plt.xlim(0,2*np.pi)
plt.savefig("cm.png")
plt.show()
黒→赤→黄色で大きくなっていく
さて、先ほどの散布図に`mpgの値に応じてグラデーションを付けてみます。
feature = 'mpg'
max_ = df_train_cy_ye[feature].max()
min_ = df_train_cy_ye[feature].min()
scale = max_-min_
plt.figure(figsize=(8,8))
for value in df_train_cy_ye[feature].unique():
condition = df_train_cy_ye[feature] == value
plt.scatter(df_train_pca[condition,0],df_train_pca[condition,1],color=cm.hot((value-min_)/scale))
plt.show()
2次曲線っぽさを感じる
先に書いたとおり、2次曲線っぽい変化をしているような印象はあります。特に黒(mpgが低い)は右上から下に下るにつれて赤みが出てくるように見えます。左側の黄色や赤は上に行くにつれ色が変わるって感じではないですね。
mpgが2次曲線っぽくなるので、'displacement'とかもそうなるのでしょうか？
※コードはほぼ同じなので省略します。
displacement,horsepower,weight
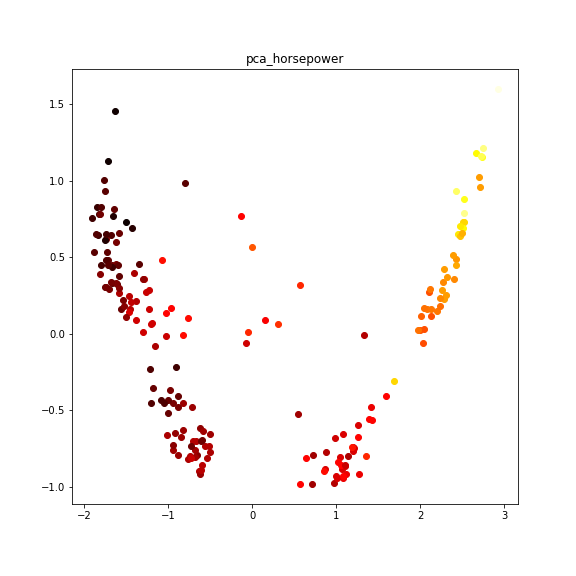
こんな感じだろうな―と思っていました。mpgの逆のグラデーションになるだろうなーは案の定ですね。
accelerationはどうでしょうか？
acceleration
やはり結構色が混ざっていますね。しかし、右ほど黒が多く、左ほど黄色が多いです。全然関係ないって程ではないですね。
cylindersとoriginはどうでしょうか？クラスタリングの時にだいたいこれで分かれていましたが…
※さっきと同じグラデーションにすると見づらくなったので色を変えました。
※カテゴリ変数が値の大きさに意味はありませんが、色分けによって違うグループであることが確認できます。黄色だから良いとかそういうことはありません。
赤が小さい、黄色が大きい
cylinders,origin
なるほど、ザックリまとまっていたのはだいたいcylindersによる影響だったのですね。originも、左上に2グループとそれ以外で1グループに分かれます。
最後にmodel_yearです。
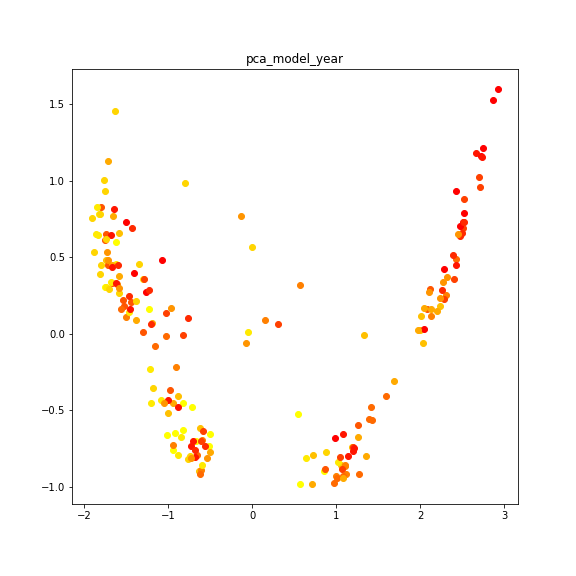
これはだいぶ散らかっているような気がしなくもないです。右側に黄色がいないですね。
影響力の高そうなcylindersやoriginを抜いたらどうなるのか？
クラスタリングの時に影響力が高く、また主成分分析でもザックリ分類してくれていた。'cylinders'や'origin'を変数から外した場合、この主成分分析にどのくらい影響が出るのだろうか？と気になったので調べます。
量的変数を標準化→cylindersとoriginを外す→Gower距離行列に変える→主成分分析で変換 と処理を行います。
※やることは以前書いたことと大半同じなのでコードを省略します。
cylindersとoriginを除くと…？
さらに2次曲線味が増しましたね。スポーツブランドのロゴにありそう。
これもどのような意味を持っているのか確認します。
同じようなグラフをたくさん出しても長いので、個人的に面白い奴だけ出します。
まずはmpgです。
pca2とmpg
（pca2とかいうナンバリングのクソ適当な命名なのは気にしないでください）
これはかなりきれいなグラデーションに見えますね。モデル予測の時にも使えそうな気がします。
…mpgを変数に使っているとモデル分析に使えないのでは？と思ったので、後でmpgも除いたバージョンも試します。displacementとかの変数でほぼほぼ再現できると思いますが。
cylindersを使っていませんが、cylindersで色分けしたらどうなるでしょうか？
pca2とcylinders
言われてみればそうなるよねーって感じがします。この曲線がmpgできれいなグラデーションを作れるので、cylindersくんがきれいに3分割できるのもそうだろうなーって感じました。
関係が薄めと思われてきたaccelerationだとどうなるでしょうか？
pca2とacceleration
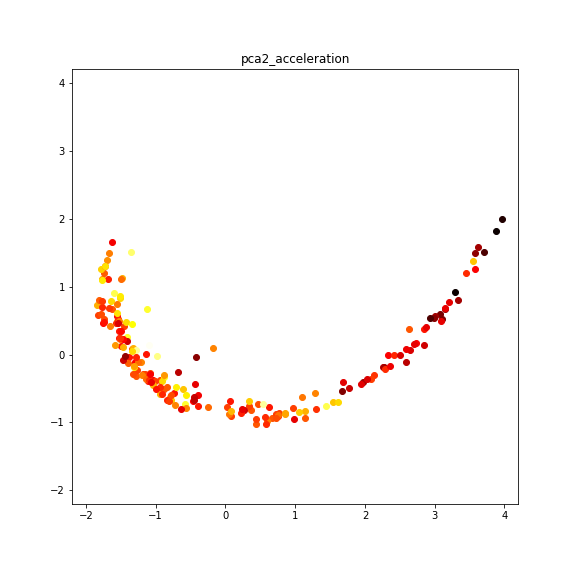
やはり色が混在していますね。もう少し色ごとの違いを見たかったので、色ごとに取り出します。
accelerationの値に応じて10段階に分けて、それぞれに色付けをします。10段階の分け方はパーセンタイル（箱ひげ図の分け方とだいたい同じ）です。境界線の値が複数あるときに等分割されませんが気にしないでください。
パーセンタイルで10等分してくれる関数
def divide_quantity_to10(samples, feature):
dividing_point = []
for i in range(10):
dividing_point.append(samples[feature].quantile(i * 0.1))
samples[f'{feature}_divide'] = 0
for i in range(10):
samples[f'{feature}_divide'] = samples[f'{feature}_divide'].where(samples[feature] < dividing_point[i], i)
# 色変えしたい変数
feature = 'acceleration'
# 10分割
df_train_divide = copy.copy(df_train_cy_ye)
divide_quantity_to10(df_train_divide,feature)
# 10段階に分けて出力
fig = plt.figure(figsize=(16,6))
plt.title(f'pca2_{feature}')
for i in range(10):
ax = fig.add_subplot(2,5,i+1)
condition = df_train_divide[f'{feature}_divide'] == i
ax.scatter(df_train_pca2[condition,0],df_train_pca2[condition,1],color=cm.hsv(i/10))
plt.xlim(-2.2,4.2)
plt.ylim(-1.2,2.2)
plt.show()
pca2とacceleration
値が小さいと右寄りで、徐々に左に移っている…？一番値が小さいときは右寄りで、値が大きいときは左寄りなのは見て取れますが、間は別に右寄りでも左寄りでもないような…。重量級の時に加速が重い奴が多いってくらいでしょうか？
回帰分析の時を考慮してmpgも外す
先に少し話題に出しましたが、目的変数であるmpgを使った変換は回帰分析をするときに使えないので、cylindersとoriginに加えてmpgも外します。
※やることがほぼ同じなのでコードを省略します。
mpgも除いてみると…？
だいたいひとつ前と同じ曲線ですね。mpgとdisplacement horsepower weightの性質がだいたい同じなので、そんな気がしていました。
一応色付けもします。だいたい同じ結果になりそうですが。
pca3とmpg
mpgが入っていない時とだいたい同じ結果になりました。
少し違うのは、2次曲線の太さがこちらの方が太く、また曲線の内側よりも外側のほうがmpgの値が大きくなっている印象があります。外側と内側の違いが分かればかなり役に立ちそうですね。
外側と内側の違いを作っているのは、どうやらmodel_yearっぽいです。
pca3とmodel_year
ぱっと見で黒が内側に多く黄色が外側に多い印象です。よく見ると黒と赤は混ざっている部分も多いですね。外側なほどmodel_yearが大きいと言ってよいのではないでしょうか？
ザックリ主成分分析のまとめ
-
mpgやdisplacementなどの値に応じてグラデーションする2次曲線のようなものが出来上がる。 -
cylindersやoriginを入れると、その値に応じてまとまりが出る。 - ↑を入れないとより2次曲線っぽさが出る。
- 曲線の内側と外側は'model_year'が作っているっぽい
T_SNE
主成分分析で私が感じたことはだいたい書いたので、別の次元削減も試します。
次はT_SNEです。詳細は割愛しますが、やっていることはだいたい主成分分析と同じです。
前処理
主成分分析と同じです。
カテゴリ変数をそのまま使えないので、Gower距離行列に変換します。量的変数だけの場合は標準化が必要です。
from sklearn.manifold import TSNE
tsne = TSNE(random_state=0)
df_train_tsne = tsne.fit_transform(df_train_gw)
T_SNEで次元削減
早速2次元に圧縮したものをグラフにプロットします。
きれいに5つの塊に分かれました。
…5つのグループ？まさかcylindersとoriginか？
cylindersとoriginだった
そんな気がしていましたが、やっぱりそうなんですね。
（いろいろ終わった後で思ったことですが、たぶんgower距離計算のおかげでカテゴリの違いがハッキリ出るんだと思います。）
一応mpgによる色分けも載せます。
左上の2つのグループは左下に行くほど、下の3グループは右下に行くほど値が大きいみたいですね。
cylindersとoriginを取り除く
主成分分析でもやったように、T_SNEでもcylindersとoriginを取り除いてみます。
うわ、きっしょ
水の流れのような何かに見えます。これも色分けしてみましょう。
tsneとmpg
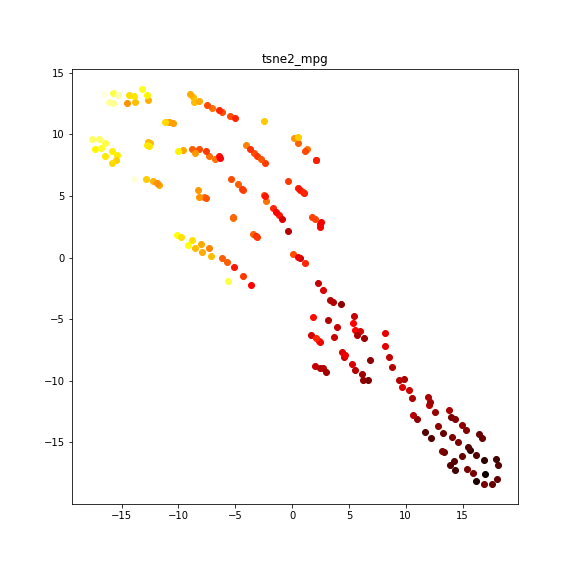
全体の傾向としては、右下ほど黒、左上に行くほど黄色になる印象です。細かく見ると、左上の赤~黄色の広がりがある部分では、つながりのある小グループごとに左上ほど黄色くなっているような感じがします。（これテキスト表現で伝わっているでしょうか？）
この広がりは何によって作られているのでしょうか？
model_yearで広がっているっぽい
model_yearごとに色分けすると、細かいグループがmodel_yearごとにくっついていることがわかります。しかし、model_yearが同じならくっつくというわけでもないようですね。わかりやすいように色ごとに出力します。
同じ色でも右下～左上に広がっていますね。性能の差でグループが分離しているような感じでしょうか。
mpgも除いてみる
主成分分析でmpgを取り除きましたが、T_SNEでもやってみます。
cylinders,origin,mpgを取り除く
mpgありと比べて、画像がひっくり返っただけのような気がします。細かく見れば、広がり方が大きくなっているような印象があります。この微妙に広がったのはもしかしたらありがたいかもしれません。
色分けもします。mpgです。
これもひっくり返せばさっきと同じ感じがしますね。左上が黒で、右下に行くにつれて黄色に変化していきます。グループごとに右下ほど黄色なのも同じですね。
ほかの色分けもさっきとほぼ同じなので割愛します。細かいグループはmodel_yearによって構成されていました。
UMAP
UMAPも次元削減の手法の一つです。やっていることはだいたいT_SNEと同じです。（同じって言うと語弊が多いような気がしますが）
前処理
主成分分析と同じです。
カテゴリ変数をそのまま使えないので、Gower距離行列に変換します。量的変数だけの場合は標準化が必要です。
import umap
UMAP = umap.UMAP(random_state=0)
df_train_umap = UMAP.fit_transform(df_train_gw)
UMAPで次元削減
早速プロットします。
UMAPで次元削減
5つの塊に分かれました。cylindersとoriginなんだろうなぁ。
それを確かめるために色分けします。
cylindersとoriginでした
そうだと思いました。次元削減にカテゴリを入れるときにはよく考えたほうがいい気がしてきました。
やはりcylindersとoriginを除きます。
cylindersとoriginを除くと…？
これはいったい何の模様でしょうか？何やら愉快なことになっていますね。ぱっと見では解釈が難しいです。
色付けをしてどうなっているのか確認してみましょう。
全体的にみると、右上が黒で左下が黄色になっていますね。全体の傾向もうまくグラデーションしていますが、塊ごとに見たほうがグラデーションがキレイです。
他の傾向もだいたいT_SNEと同じでした。
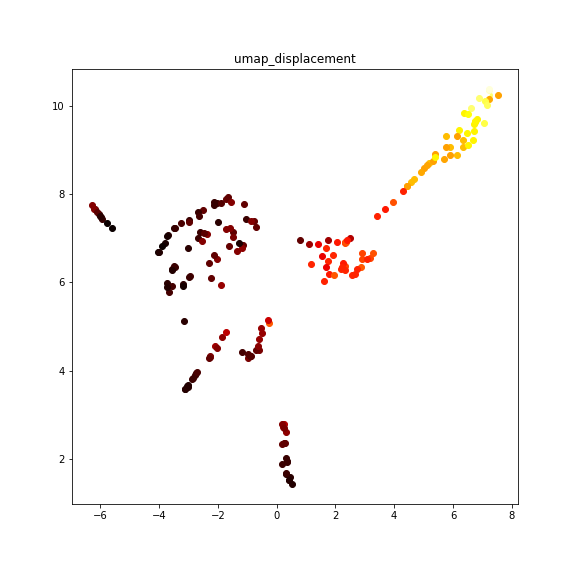
mpgも除く
やはりmpgも除いて試します。
なんかすっきりしたような気がします。
色付けしてみましょう。
他の手法と違い、きれいなグラデーションとはいかないようです。全体的には、右下が黒、中央が赤、広がると黄色、とかそんな感じでしょうか？そうでもない…？
他のグラフも見てみます。
displacement
horsepower
weight
acceleration
cylinders
origin
model_year
ザックリ傾向は他の手法と同じような気がします。
次回に続きます。
今回は次元削減を使いました。割と面白い結果になったなと個人的に思っています。次元削減をうまく使えば回帰予測にも役立ちそうです。
次回はようやく本題の回帰分析です。線形回帰とか、RandomForestとか、LightGBMとかを使って燃費を予測します。その中に今回の次元削減を取り入れたりとか、やれそうなことはいろいろあります。全部終わるまでまだしばらくありそうです。