こちらの記事をご覧いただきありがとうございます。
機械学習についていろいろ勉強している中で、時系列データの分析に関心を持つようになりました。
その練習としていずれ天気予報をしてやろうと思っていますが、その事前準備として時系列データの分析の基本を勉強してきたので、ここにまとめます。
勉強のアウトプットとして書くので見づらい部分もあると思いますが、ご覧いただいた皆様にも学びがあれば幸いです。
詳しく説明すると記事が長く見づらくなってしまうので、この記事では各要素を簡潔にまとめる程度にしています。あと自分がまだそんなに詳しくない。
詳しく知りたい項目があれば各自で調べてみてください。私が参考にしたものはなるべくリンクを貼っておきます。
参考
以下を存分に参考にさせていただきました。
この記事でまとめられていることは、ほぼほぼこの参考資料にまとめられていることと同じです。
時系列データって何ですか？
時間で変化するものを観測したデータのこと
私が分析しようとしている気象情報はその最たる例だと思いますが、時間の流れとともに変化するものを、時間も一緒に記録したデータを「時系列データ」と言います。
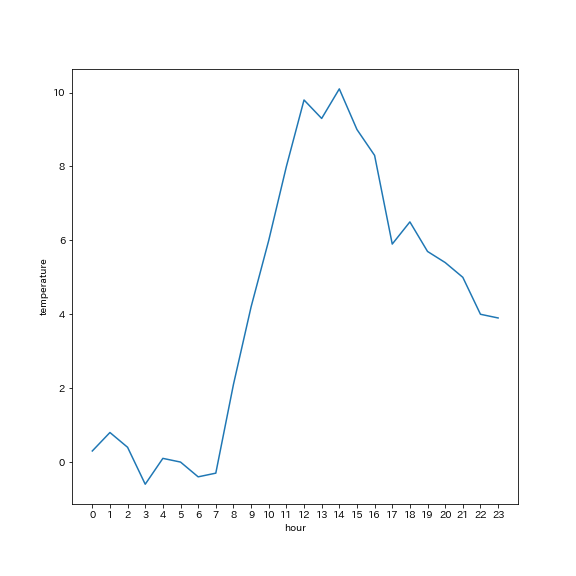
大抵は、x軸に時間を、y軸に観測値を持つ折れ線グラフで、時間による変化を見ることができます。
例：2021年1月1日の気温変化
多変量時系列
時系列データの中でも、同じタイミングで複数のデータを記録したものを「多変量時系列」と言います。
下は気象庁から公開されている気象情報データです。分析のためにもらってきました。
※気象庁のデータはこちらから拝借しました
気象情報データ（加工済み）
時系列データから得られる情報
長期的に見るか、短期的に見るか
データの何を知りたいかによって、情報の取り出し方が変わります。
長期的に見る場合、例えば天気なら、2000年～2020年の東京の気温がどう変わったかを見たい場合などは、小さな変化を取り除いて「 トレンド 」に注目します
短期的に見る場合、例えば天気なら、昨日から今日までの気温の変化を見たい場合などは、長期的な変化を取り除いて「 短期的変動 」に注目します。
視点がミクロかマクロか、みたいな表現をしてもいいかもしれません。
トレンド
長期的な傾向の変化のこと。
天気でいえば、地球温暖化は「気温のトレンドが上昇傾向である」と表現してよいでしょう。
1日2日の変化ではなく、継続して変化し続けている様子です。
例：2021年の気温のトレンド
取り出し方：移動平均
特定の時間とその周辺の時間の平均をとる手法です。
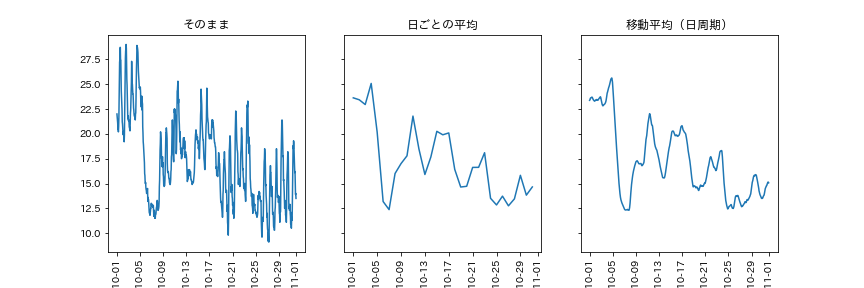
例えば1時間ごとに観測した気温データがあったとして、 12月1日12時の観測値を12月1日0時～12月2日0時の平均値に置き換える 、といった形で、全ての観測値を周囲12時間の平均に置き換えます。
これによって1日の中での気温の変化が均され、季節によって徐々に変化する気温を眺めることができます。（トレンドを含む点に注意）
気温を1日単位で移動平均(2022年10月)
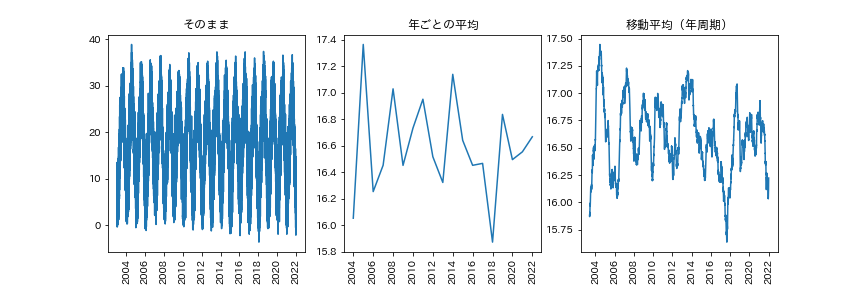
平均する範囲を年単位にすれば、年内の気温変化が均されるので、季節変化がなくなってトレンドを眺めることができます。
気温を1年単位で移動平均(2003年～2021年)
短期的変動
短期的な変化のこと（まんまじゃないか）。
気温でいえば、今日は特に暑かったな～みたいな感想が出てきたら、それは「気温の短期的変動で暑い」と表現できます。
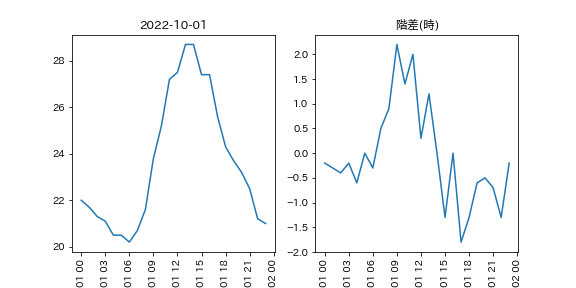
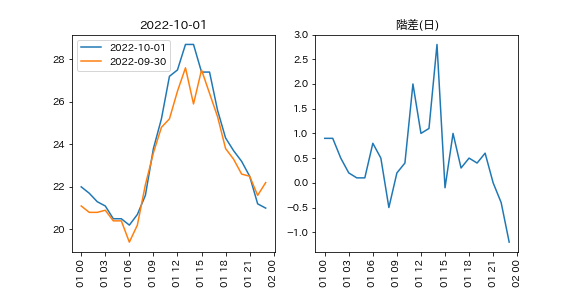
取り出し方：階差
特定のの時点の値からひとつ前の時点の値を引いた値のこと。
気温なら、「12月1日午後3時の気温の階差」は 12月1日午後3時の気温から12月1日午後2時の気温を引いた値 です(1時間ごとの観測なら)。
気温を階差に変換(2022年10月1日)
気温を階差に変換(2022年10月)
※経済分野では差ではなく比を用いることが多いらしいです。株価の収益比とか。
スケールの差に影響される変化なら比を取ると有効です。大抵は対数の差（実質比の計算）が用いられる気がします。
取り出し方：季節階差
データに周期性がある場合、その周期に合わせて階差を計算します。
例えば、気温なら1日ごとに周期性があるので、「12月1日午後3時の気温の階差」を 12月1日午後3時の気温から11月30日午後3時の気温を引いた値 にします。
これによって前日と比較しているデータを眺めることができます。
気温を日の季節階差に変換(2022年10月1日)
昨年との比較にしたいのであれば、ちょうど1年前の同じ時間との差を取ればいいですね。
気温を年の季節階差に変換(2022年10月1日)
気温を年の季節階差に変換(2022年10月)
ボラティリティ
データの振れ幅のこと。
振れ幅が大きいなら「ボラティリティが大きい」と表現できます。
分散の大きさをそのままボラティリティと表現できるかもしれません。
※私が調べた限りでは、ボラティリティは経済用語感が強い気がします。
経済の動向を調べるための時系列分析の用語がそのまま経済以外でも普及したのではないでしょうか？（知らんけど）
ボラティリティが大きい小さい
(画像はネット上に落ちていたものを拝借しました)
ノイズ
不要な情報のこと。見たい情報ではない情報と言ってもよいです。
トレンドを見たい場合は短期的変動がノイズとなり、短期的変動が見たい場合はトレンドがノイズになります。
※時系列では白色雑音と呼ばれるものがありますが、それとは区別されるものです。
時系列の周期
周期的変動
一定間隔で同じような変化を繰り返す変化のこと。
気温でいえば、1日の気温変化や1年の季節による気温変化は周期的変動ですね。
1年周期の周期的変化は特に季節変動と呼ばれます。
例：1日の気温の周期的変化(2022年10月1日~7日)
現実の周期的変動は徐々に周期がずれていくパターンが多いようです。
地球の自転速度も徐々に遅くなっているとかなんとか。(こちらを参考)
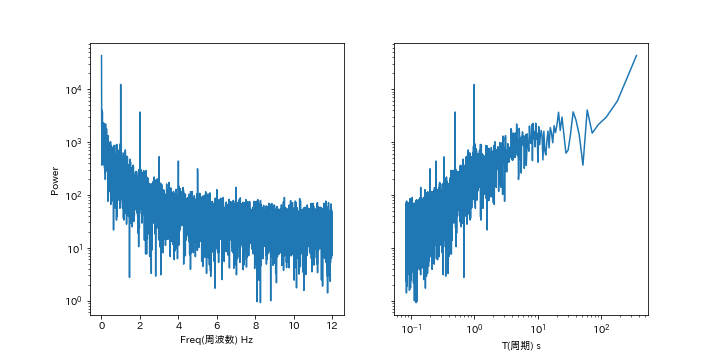
スペクトル分解（時系列を複数の周期関数に分解する）
時系列データが複数の周期的変動の要素を持っている場合に、周期の波を一つ一つ取り出します。
時系列データをフーリエ変換するとスペクトルに、スペクトルをフーリエ逆変換すると時系列データになるんだそうです。
詳しくは以下をご覧ください。
スペクトル分解
具体的なやり方の解説
例：気温をスペクトル分解(2021年)
例：気温の階差（時）をスペクトル分解(2021年)
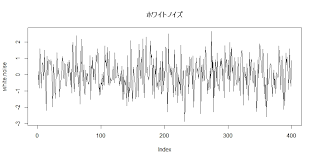
白色雑音
あらゆる周期の波を同じ割合で含んでいる波のこと。
特に時系列データでは時間に相関がない情報を指しており、時系列モデルを作る場合は残差が白色雑音になるようにします。
時間に関係のあるデータはちゃんと式として再現しようってことですね。
白色雑音の例
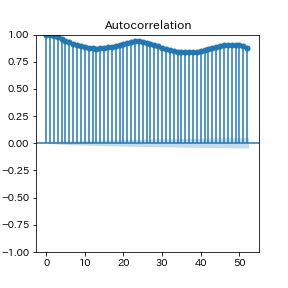
自己相関（係数）と自己相関関数
ある時間の値とそのk時点前の時間の値の相関(係数)のこと。
相関係数が大きい(1か-1に近い)ほど、今の値は過去の値と関連が深い（時間の影響がある）と言えます。
相関係数が小さい(0に近い)ほど、時間と関係が薄いです。
気温の自己相関(時)
また、相関係数を時間差の関数とする自己相関関数があります。
グラフに直すとコレログラムです。
例：気温の自己相関関数(2003年~2018年)
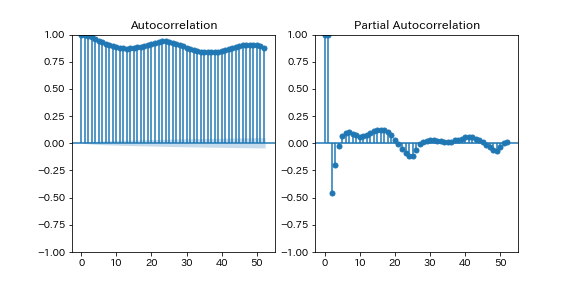
偏自己相関
例えば、気温は1時間前と強い相関があるのはそうだとして、2時間前との相関を考えた時に、1時間前と2時間前が強い相関があるので、今と2時間前で強い相関があって当然のような気がしませんか？
今と2時間前の相関を計算する時に、2時間前が1時間前から受けている影響をなくして計算しているのが 偏自己相関 です。
自己相関（左）と偏自己相関（右）
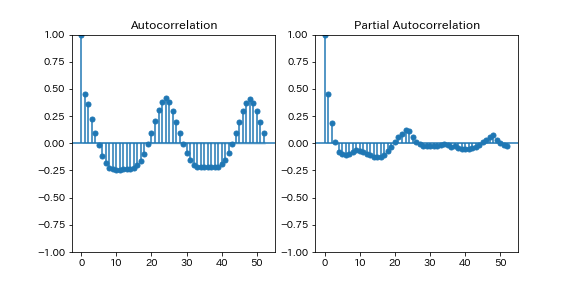
階差と自己相関関数
時系列データを階差に変換してから自己相関関数に変換すると、結構結果が変わります。季節階差でも同様です。
だいぶ印象が変わると思うので、気になるものは一通り確認しておくと良いのではないでしょうか。解釈の仕方だけ気をつけましょう。
気温の階差（時）と（偏）自己相関関数
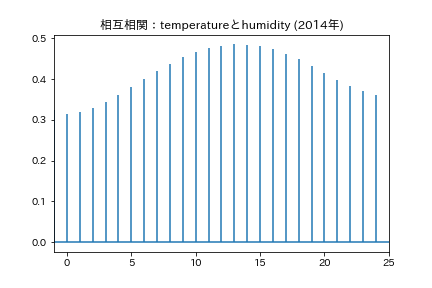
相互相関（関数）
多変量時系列の場合の、他の変数のk時点前のデータとの相関係数のこと。
1(-1)に近いと関係が深いと言えます。
※因果関係があるという訳ではないので注意
気温と湿度の相互相関関数(2014年)
季節調整
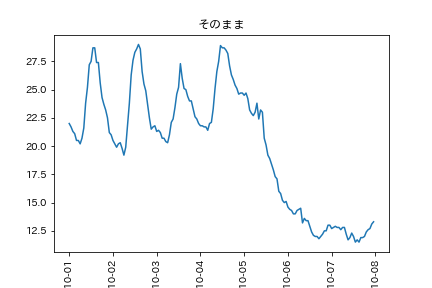
時系列データを眺めるとき、そのまま折れ線グラフにして眺めてもいまいち解釈に困ることがあります。
もしくは、ぱっと見では気が付きにくい情報が隠れているかもしれません。
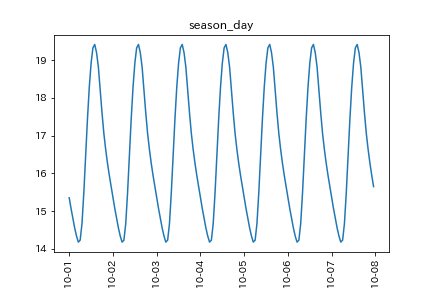
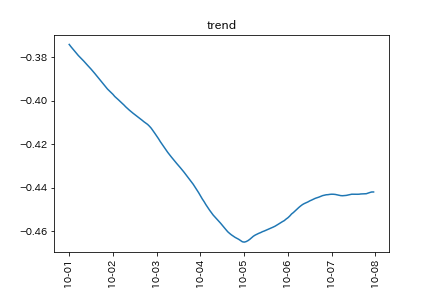
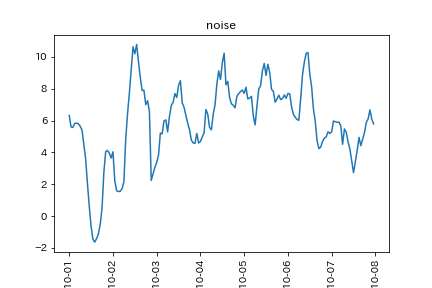
そんな時に、先にも挙げた「トレンド」や「季節成分」に分けてから観察すると、かなり眺めやすくなります。
※例は季節成分で日周期だけ取り出していますが、この場合にノイズに年周期の変動が入り込みます。
周期が複数あるなら分けて取り出せるのが望ましいです。
例：気温データの分解(季節成分は日周期のみ)
季節調整の手法
季節調整では、元の時系列データをトレンドと季節成分と不規則成分の3つに分けることを考えます。
かけ算に分解されることが多いような気がしますが、これはやはりスケールの変化に対応できるようにするためです。
$ 時系列データ = トレンド + 季節成分 + 不規則成分 $
または
$ 時系列データ = トレンド × 季節成分 × 不規則成分 $
以下は基本的な手法であり、古典的と言われることもあるものです。
こちらで紹介されている手法です。
最初に季節成分を取り出します。
これは周期ごとに分割してそれぞれの平均を計算して、周期の回数分だけ平均値を並べます。
例えば1日周期の気温の変化であれば、0時の気温の平均、1時の気温の平均、…23時の気温の平均、と計算します。
気温の季節成分（日周期）
次にトレンドを取り出します。
元の時系列データから季節成分を引き（掛け算に分解するなら割る）、引いた後のデータで移動平均を計算します。
気温のトレンド成分
最後に、元の時系列データからトレンドと季節成分を引く（割る）と、不規則成分が残ります。
気温の不規則成分
以上が基本的な手法です。
これを発展させた手法もあります。こちらでいくらか紹介されています。
時系列データの将来予測
天気予報をするなら、 今 の気象情報から 少し先 の天気が予測できる必要がありますね。
ビジネスっぽい話なら、今までの業績を維持すると将来の売上は～とか、株価の変動が～とか、そういうことができるとかなり役立つはずです。
例：気温を予測
ARモデル：過去データから現在の値を予測する
将来予測の手法はいろいろあるっぽいですが、（おそらく）最も基本的な手法がARモデルです。
ARモデルでは、今の値は過去の値によって決まることを式で表現します。
$ 今 = a × 1時点前 + b × 2時点前 + … + n × m時点前 + ノイズ $
aとかbはうまいこと妥当な数字を探します（後術）。
気温を例にすると、↓のようになります。
$ 今の気温 = a × 1時間前の気温 + b × 2時間前の気温 + … + n × m時間前の気温 + ノイズ $
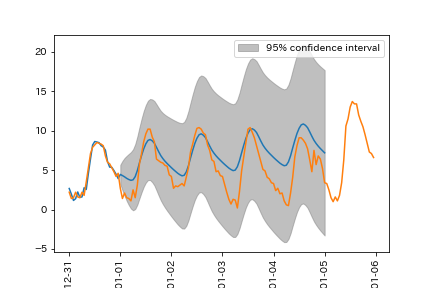
これを使って、
$ 1時間後の気温 = a × 今の気温 + b × 1時間前の気温 + … + n × (m-1)時間前の気温 $
とすると、1時間後の気温が予測できます。
また、予測した値を使って
$ 2時間後の気温 = a × 1時間後の気温(予測) + b × 今の気温 + … + n × (m-2)時間前の気温 $
とさらに先の予測ができ、理論上いくらでも先の予測でもできます。
（先になるほど予測のズレが大きくなりやすいですが）
パラメータ推定
で、aとかb（係数）のうまい探し方にYule-Walker法というものがあります。
予測誤差分散の期待値を最⼩にするように係数を決める手法です。
※ほか最小二乗法や最尤法とかでも可能です。
簡潔な説明をするには少々ややこしい話なのでここでの解説は割愛します。
こちらが詳しいのでぜひご覧ください
もしくは、使うだけなら専用のライブラリを利用すればいいので、いったん理解を飛ばすのもよいと思います。
モデルの次数
次数とは、予測のために何時点前までのデータを利用するか、ということです。
気温でいえば、今の気温を予測するために1時間前が分かれば十分なのか、1日前くらいまで欲しいのか、とかそんな話です。
たくさんあればその分良くない？と思うかもしれませんが、詳しすぎるとかえって予測精度が悪くなることが多いです（過学習）。
扱う時系列データによって必要な次数も変わります。
次数決定のためによく用いられる指標が、 AIC というものです。
説明は割愛します。こちらなどぜひご覧ください。
将来予測の前処理
データをそのまま時系列モデルにぶち込んでも予測は可能ですが、精度が良くないこともしばしば起こります。
うまいこと予測できるように、以下のような前処理がよく利用されます。
解釈が変わる点だけ気を付けてください。
- 変数変換
- 階差（差分）、季節階差
- 前期比・前年比
- 移動平均
- 欠測値・異常値処理
気温をそのまま予測（青が予測値、橙が真値）
気温の階差を予測（青が予測値、橙が真値）
階差を気温に戻して予測（青が予測値、橙が真値）
時系列（など）分析用ライブラリ：statsmodels
pythonで時系列分析を行うなら、 statsmodels を利用すれば必要な機能はそろっています（まだ試してないけど）。
web検索で時系列分析例を探すと大抵statsmodelsを利用していました。手軽に分析するならこれで良いでしょう。
計算の理論からよく身に付けたいなら、自作で理論通りの計算コードを書くのもよいと思います。
終わり。
いかがだったでしょうか？
概要だけだったのでこれだけでは十分な理解ではないと思いますが、全体図のイメージになっていれば幸いです。
これを参考にして必要な知識を適宜補っていただければ、時系列分析はある程度何とかなる…はず。
気象データ分析をしてみようと思い立ってから、実際にデータを集めて、時系列データ分析の手法を勉強して、分析手法を一通り使ってみて、ってやっていたら結構日がたっていました。
何をするにも準備から始めて扱いに慣れるまでは結構時間がかかりますね。慣れてしまえばあとは大したことないことが多いんですが…。
して、ここからは気温だけでなく他の気象情報の分析を進めます。
気温のコードを取り回す前提で書いたのでそこまで時間はかからないような気がします。
最終的には明日の気温とか天気とかがそれなりの精度で予測できるようにしたいですね。