動作環境
以下の環境でシミュレーションを行いました.
| 項目 | バージョン |
|---|---|
| ubuntu | 22.04 |
| ROS | ROS2 humble |
はじめに
事前に設定された経路に対して,障害物を避けながら追従制御を行うシミュレーションを紹介します.車輪型ロボットの障害物回避には,ポテンシャル法やDWA(Dynamic Window Approach)などが一般的に使用されますが,今回はよりシンプルな計算手法を用いた論文[1]のアプローチを参考に実装しました.
ロボットの経路追従方法
本実験では,Pure pursuit法に基づいて移動ロボットを目標経路に追従させます.
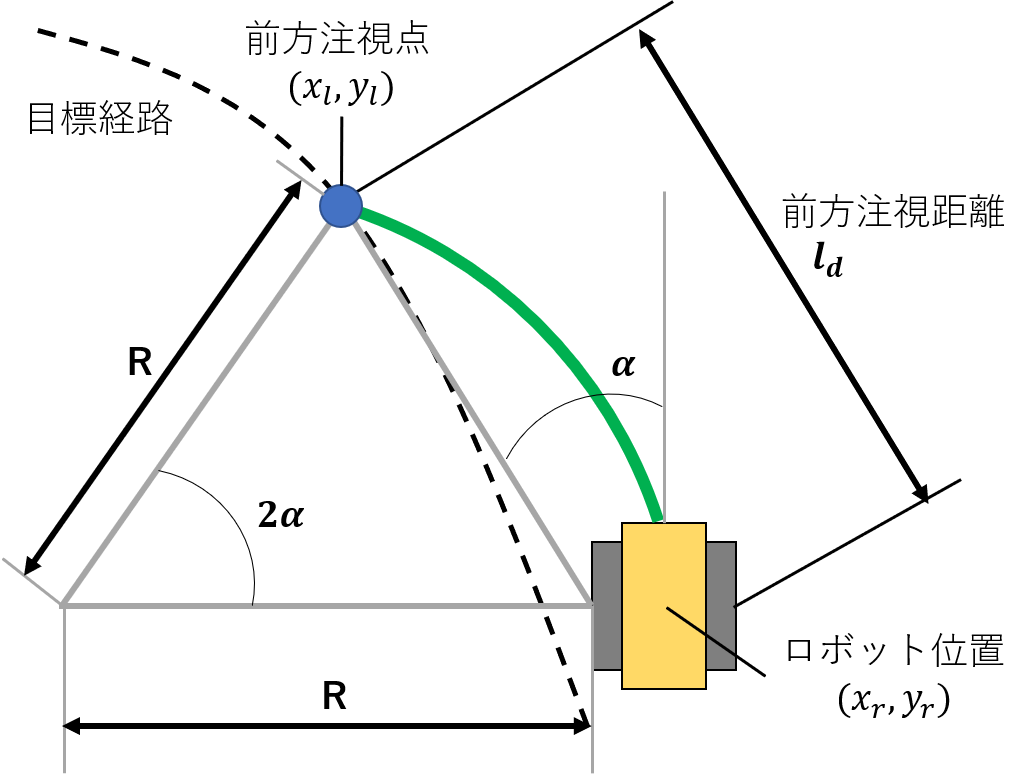
ここで,Pure pursuit 法とは, 並進速度 $v_r$ 及び前方注視距離 $l_d$ に対し, 並進速度 $v_r$ で移動ロボットの現在位置 $\left(x_r, y_r\right)$ から $l_d$ 先の経路上の点,前方注視位置 $\left(x_l, y_l\right)$ へ向かうための旋回制御手法です.
Pure pursuit 法を用いて, 制御入力 $v, \omega$ と旋回半径 $R$ をつぎのように与えます.
\begin{equation}
\begin{aligned}
v & =v_r \\
\omega & =\frac{2 v \sin \alpha}{l_d} \\
R & =\frac{v}{\omega}=\frac{l_d}{2 \sin \alpha}
\end{aligned}
\end{equation}
ここで, $\alpha$ は次のような, 目標方向ベクトルと現在の方向ベクトルのなす角です.
障害物回避を考慮したPure Pursuit法
障害物を回避させる方法として,前方注視点を障害物を中心とした円上に移動させる方法を用います.
1, 障害物回避行動のトリガーとなる条件
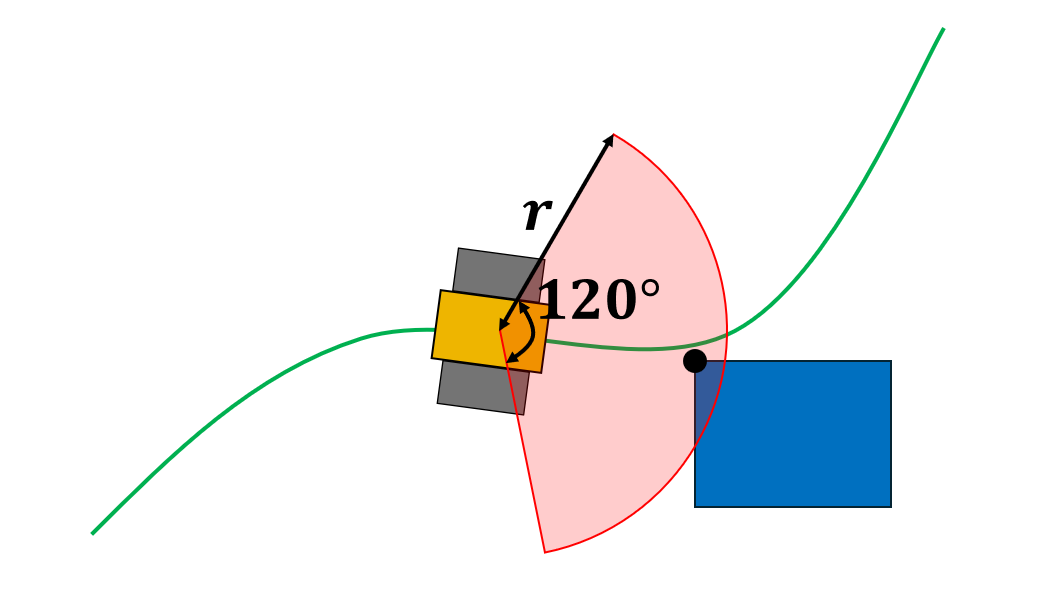
障害物回避開始の条件として,ロボットを中心に前方r[m],120度以内の扇形領域に存在する障害物の最接近点 $\left(x_o, y_o\right)$ が検出された場合とします.
2, 障害物回避のアルゴリズム
障害物回避を考慮したするため,下の図に示すように, 中心が障害物の位置 $\left(x_o, y_o\right)$ で半径が $t h$ の円 $C_o$ の円周上に前方注視点を移動させます. $t h$ は予め設定しておく障害物回避開始閾値です. 前方注視点 $\left(x_l, y_l\right)$ の決定方法は, 中心がロボットの位置 $\left(x_r, y_r\right)$, 半径が前方注視距離 $l_d$ の円 $C_r$ と円 $C_o$ の交点で, 1 サンプリング時間前の前方注視点との距離が近い側の点を前方注視点と定めます.ここで,再定義される前方注視点の座標 $\left(x_l, y_l\right)$ は以下の式で求められます.
\begin{aligned}
& y_l=\frac{-B \pm \sqrt{B^2-4 A C}}{2 A} \\
& x_l=\frac{y_r-y_o}{x_o-x_r} \cdot y_l+\frac{l_d^2+x_o^2+y_o^2-t h^2-x_r^2-y_r^2}{2 x_o-2 x_r}
\end{aligned}
ここで, $A, B, C$ はそれぞれ,以下のとおりです.
\begin{aligned}
& A=1+\left(\frac{y_r-y_o}{x_o-x_r}\right)^2 \\
& B=-2 y_r-2 x_r \frac{y_r-y_o}{x_o-x_r} \\
& +\frac{y_r-y_o}{x_o-x_r} \cdot \frac{l_d^2+x_o^2+y_o^2-t h^2-x_r^2-y_r^2}{x_o-x_r} \\
& C=x_r^2+y_r^2-l_d^2+\left(\frac{l_d^2+x_o^2+y_o^2-t h^2-x_r^2-y_r^2}{2 x_o-2 x_r}\right)^2 \\
& -x_r \cdot \frac{l_d^2+x_o^2+y_o^2-t h^2-x_r^2-y_r^2}{x_o-x_r}
\end{aligned}
再定義した前方注視点をもとに,式(2),(3)から$v, \omega$を目標並進速度$v$,目標回転角速度$\omega$を求め,式(1)から左右輪の目標回転角速度$\omega_L, \omega_R$に変換し、ロボットの車輪を制御します。

3, 障害物回避処理から, 目標ルートへ復帰する条件
障害物の回避行動を行った後, 元の目標ルートに復帰させるように, 2つの条件を設けます.
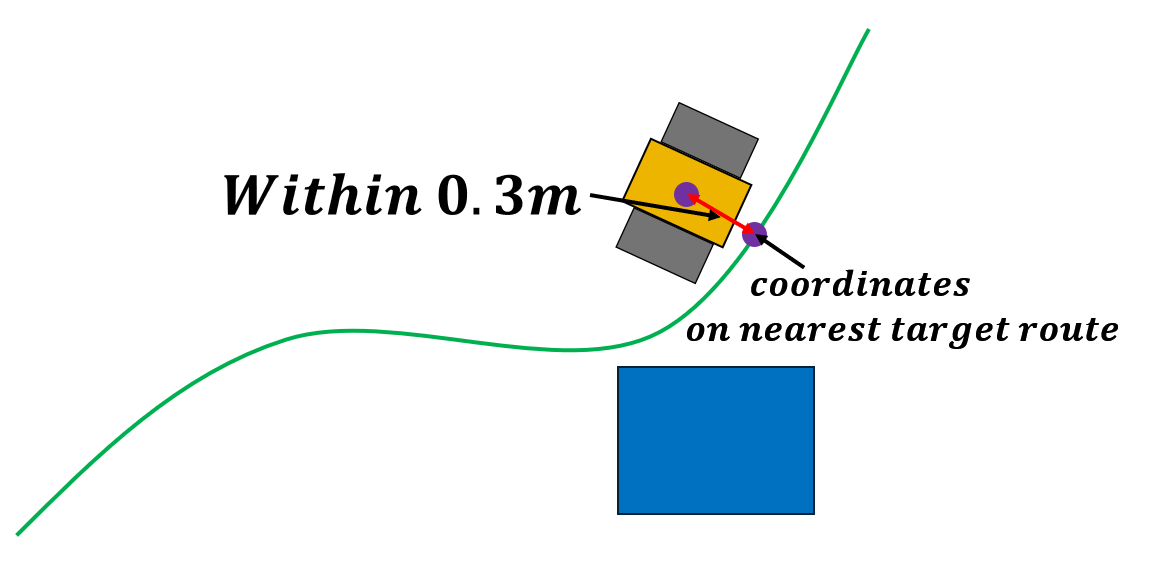
条件1 ロボットの現在地とロボットに最も近い目標ルート上の座標との距離が0.3m以内
条件2 回避行動開始地点とロボットに最も近い目標ルート上の座標との距離が0.5m以上

この2つの条件を満たすと, 回避処理が終了し, 前方注視点が目標ルートへ移動します.ロボットは目標ルートへ復帰します.
実装
以上の理論を実装したコードは, 以下のGitHubで公開しています. このコードでは, オドメトリによる自己位置推定と, 事前に設定された経路座標および障害物の座標をもとに, 障害物回避を考慮した経路追従をシミュレートしています.
経路の最適化問題を解いているわけではないので, 必ず最短経路を走行することはできませんが, 障害物を円を描くように安定して回避しています. 障害物を回避した先に建物などの大きな壁が存在した場合には、元の経路に戻ることが難しくなるため, そこは別途例外処理が必要だと思います.(例えば, 避ける方向の先に更に障害物が存在するかを回避前に判別しておくなど)
次回は実際のロボットで, この障害物を回避するアルゴリズムを実装したときに, シミレーション通り障害物を回避させることができるか検証したいと思います.
ソースコード
参考文献
[1] 築城 大知, 坂口 聡範, 越智 亮太, 山本 薫: Pure pursuit法を用いた移動ロボットにおける滑らかな障害物回避手法の提案, 第64回自動制御連合講演会, 746/750(2021)
謝辞
この取り組みは, GxP(グロースエクスパートナーズ)株式会社様のサポートを受けて実施しています. 貴重なアドバイスや, ロボットに必要な機材の支援をいただきました. 心より感謝申し上げます.