※こちらは，会社の技術ブログとのクロスポスト記事です．元の記事はこちら

この記事では，Latin hypercube sampling (LHS) を調査します．
LHSによって生成される点群の性質と効果を視覚的，数値的に見ていきます．
利用したプログラムは，こちらで公開しています．

はじめに

LHSは，ランダムに点群を生成する方法の1つです．
最適化スタート時の初期解生成において，Random samplingの代わりにLHSを使う場合があります．
Efficient Global Optimization，ベイズ最適化，サロゲート進化計算などで良く利用されます．
これらの最適化アルゴリズムは，応答曲面法による推定モデルを利用します．
Random samplingよりLHSを利用した方が，構築した推定モデルの精度が良いと言われています．

この記事では，LHSによって生成される点群の性質と，点群から推定した応答曲面の精度を調査します．

点群の性質

LHS及びRandom samplingによって生成される点群を調査します．
点群は，以下のMATLABプログラムで生成します．

  N = 50; D = 2;
  X1 = rand(N,D);
  X2 = lhsdesign(N,D);
  [~,X3] = sort(rand(N,D),1);
  X3 = (rand(N,D)+X3-1)/50;

2次元の点群を各50個生成しています．

X1は，メルセンヌ・ツイスターを利用する関数randで生成された点群です．
X2は，関数lhsdesignで生成された点群です．
X3は，lhsdesignではなくrandを利用したLHSによって生成された点群です．

X2とX3は，同じ性質を持つことが期待されます．
X1は，比較のための一般的なランダムな点群です．
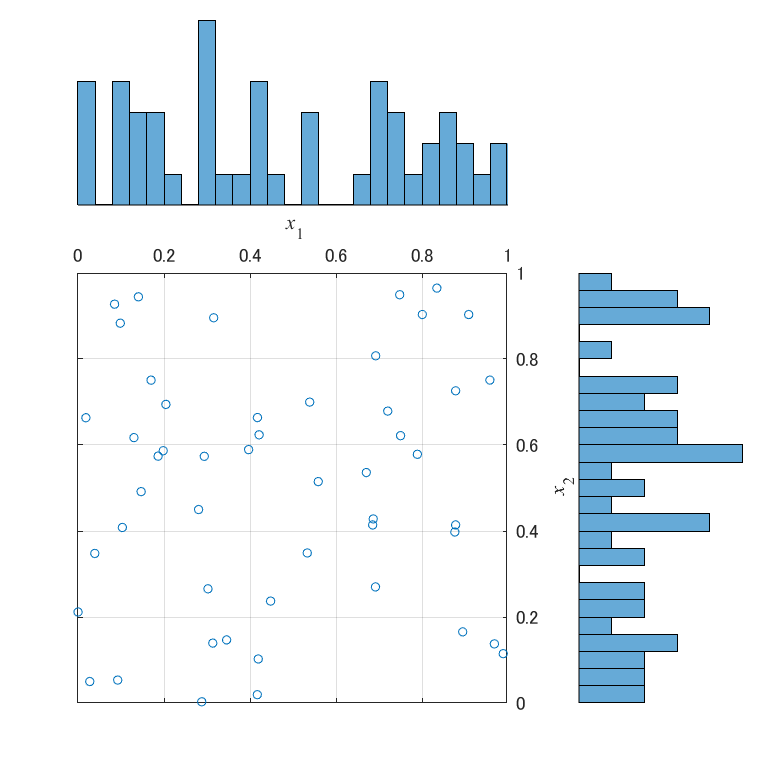
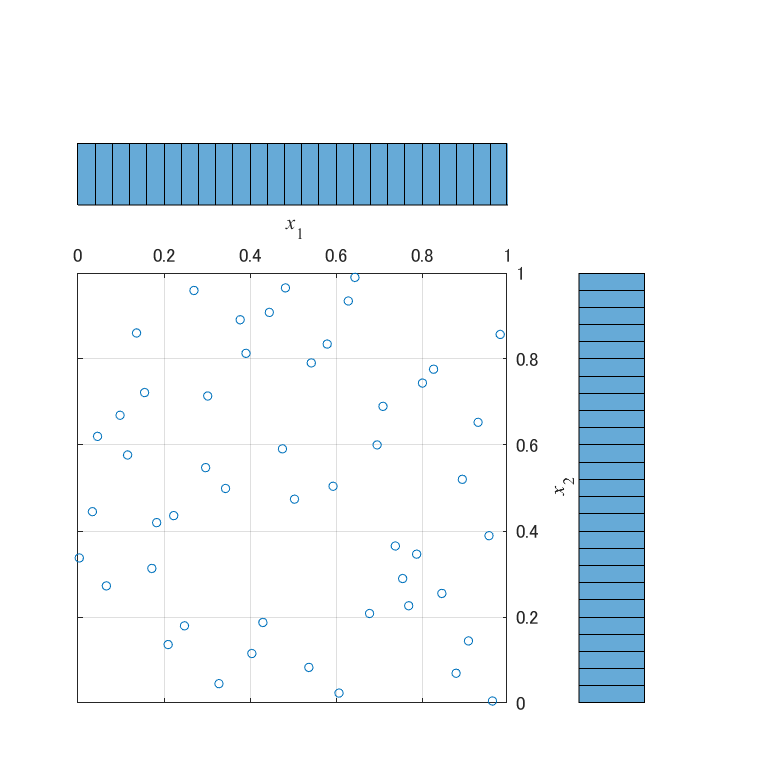
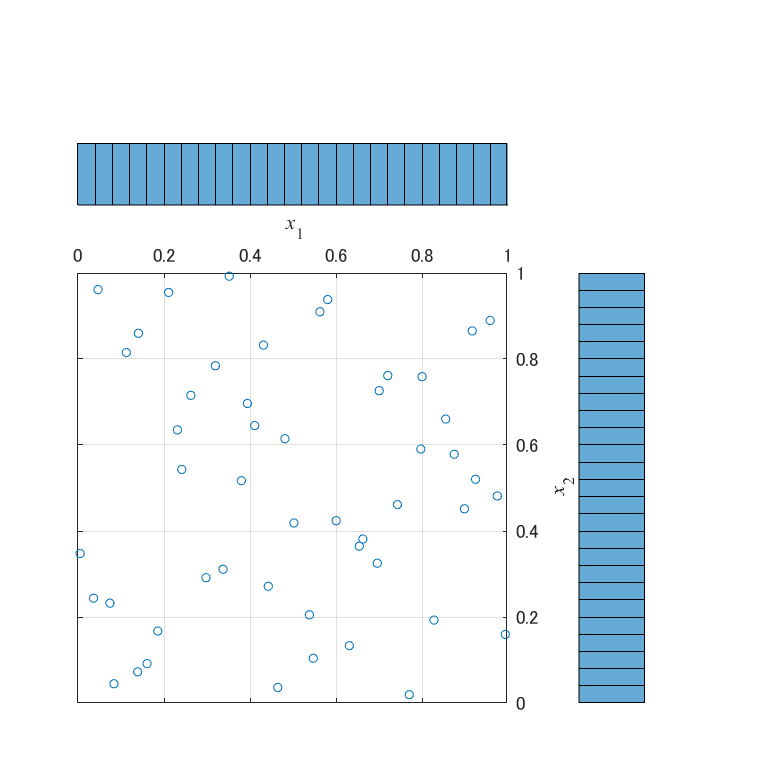
生成した点群を散布図と周辺ヒストグラムでプロットすると，以下の図が得られます．

周辺ヒストグラムは，ビンの数が25で，0.04の間隔で境界が存在します．
図から，X1は点群が空間全体に分布しているものの，空間を細かく区切ってみると粗密の偏りがあることが読み取れます．
$x_1=0.6\pm0.04$の範囲には点が存在しませんが，$x_1=0.3$近辺には6個の点が存在します．
$x_2$にも同様に偏りがあり$x_2=0.8$近辺には点が1個しか存在しません．
一方，X2とX3は，空間を細かく区切ってみても，粗密の偏りが存在しません．
空間を軸に沿って50分割した時，1つの空間に必ず点が1個分布しています．
これは，LHSによって生成される点群が持つ，特徴的な性質になります．

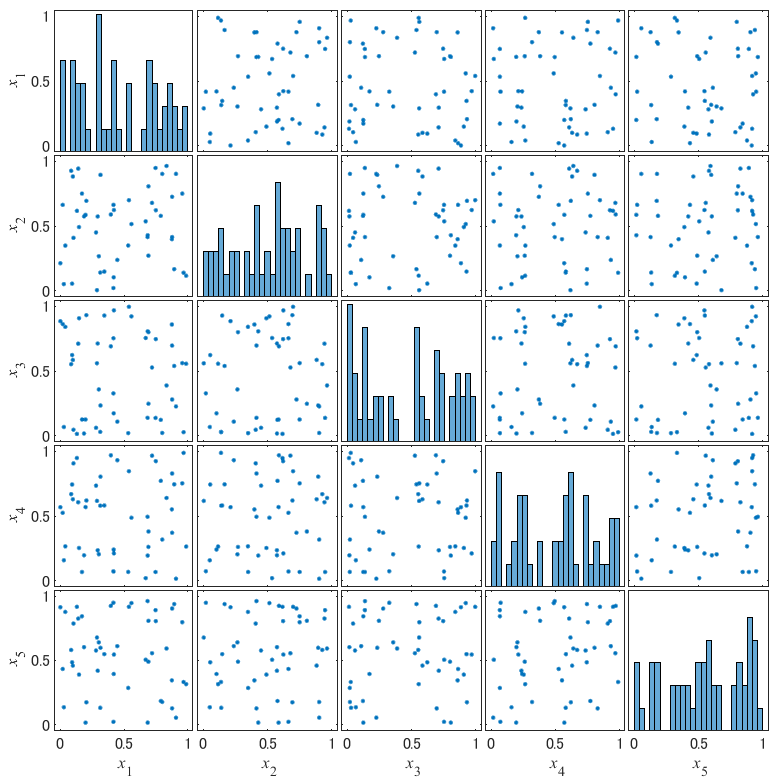
次元数を2⇒5に変更した場合も確認しましょう．
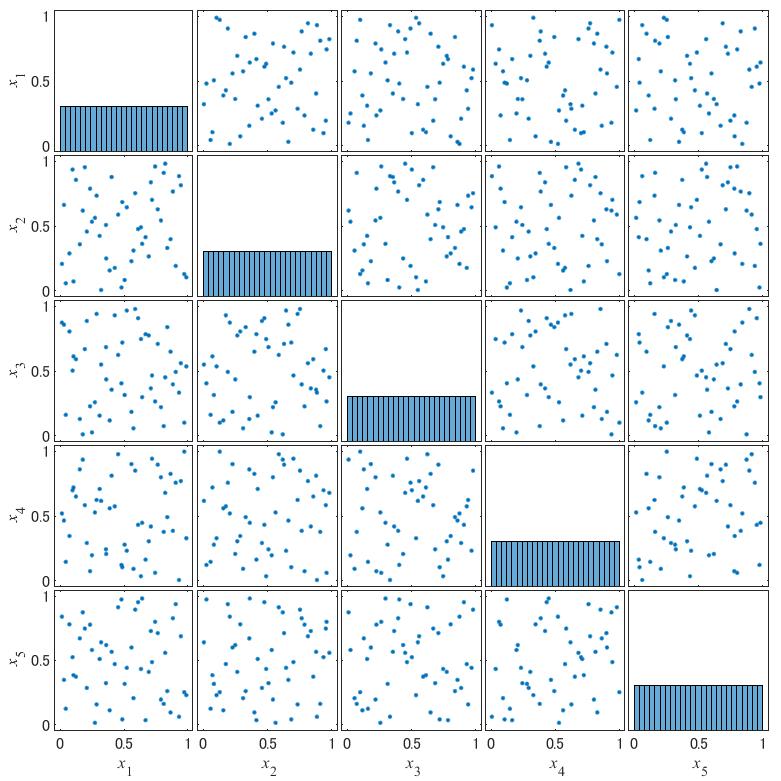
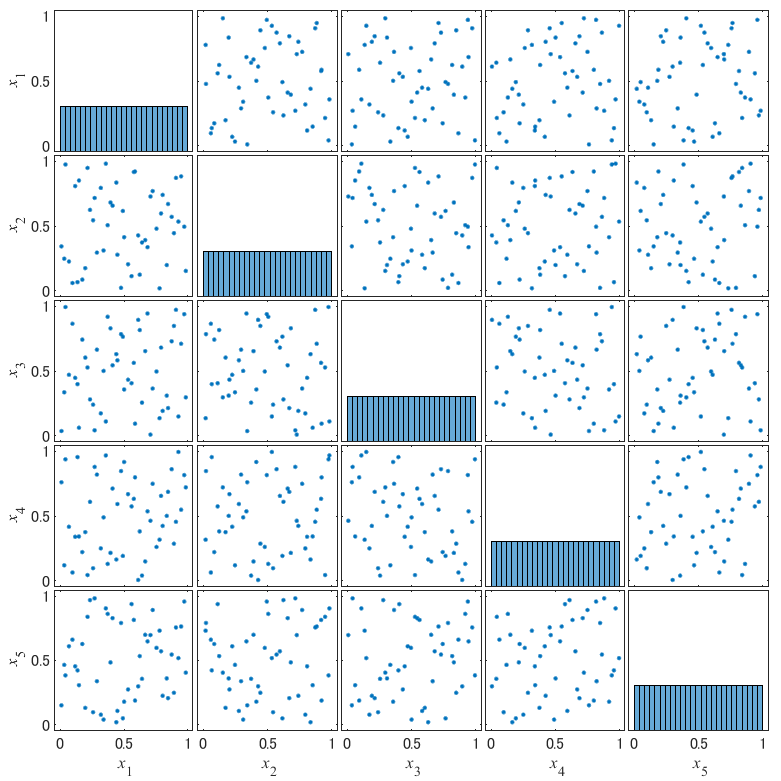
MATLABで作成した5次元の散布図行列は，以下になります．

図から，次元数が大きくなったとしても2次元の場合と同様の性質を持つことが確認出来ました．

点群から推定した曲面（RBNN）

ここでは，sin波を足し合わせた曲面を推定します．
まず，点群Xの各座標$(x_1,x_2)$から，その高さを求めます．
次に，高さを推定したい地点の集合，点群Yを用意します．
今回は，$100\times100=10,000$の格子点群をYとします．
そして，応答曲面法で点群Yの各地点の高さを推定します．

応答曲面法として，Radial basis neural network (RBNN) を採用します．
点群Yの高さ（真値），誤差（推定値と真値の差）も計算します．

  XH = sum(sin(X.*10),2);       % 点群Xの高さ
  [x1,x2] = meshgrid(0:1/99:1); % 2次元の格子座標
  Y = [x1(:),x2(:)];            % 点群Y

  EH = sim(newrbe(X',XH'),Y')'; % 点群Yの高さ（推定値）
  YH = sum(sin(Y.*10),2);       % 点群Yの高さ（真値）
  disp(sum(abs(EH-YH),'all'));  % 誤差（推定値と真値の差）の合計を表示

関数newrbeを利用するには，Deep Learning Toolboxが必要です．
推定した応答曲面と誤差（真値と推定値の差）の合計は，以下になります．


X1: 496.1693	X2: 174.7704	X3: 286.9724

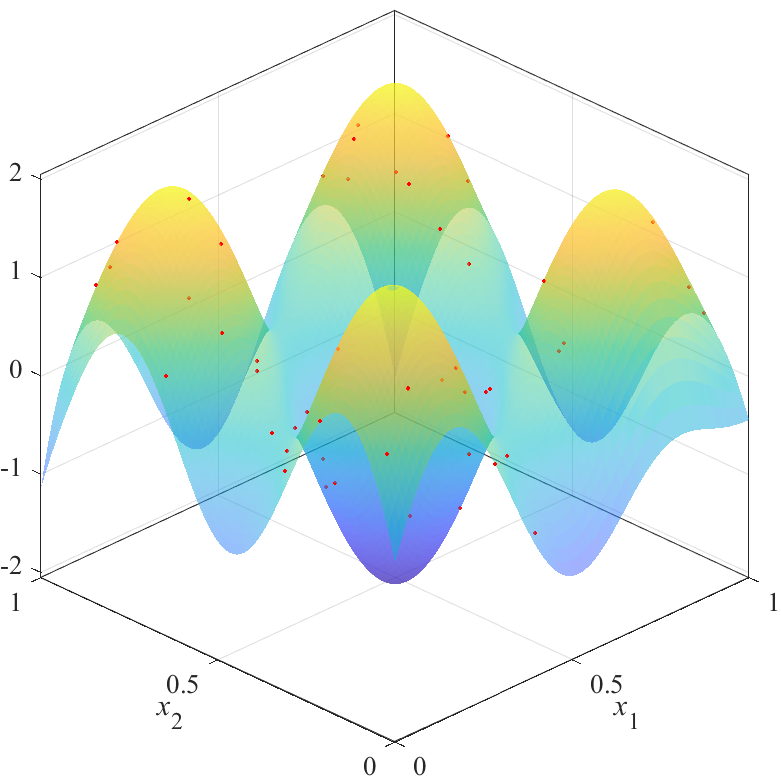
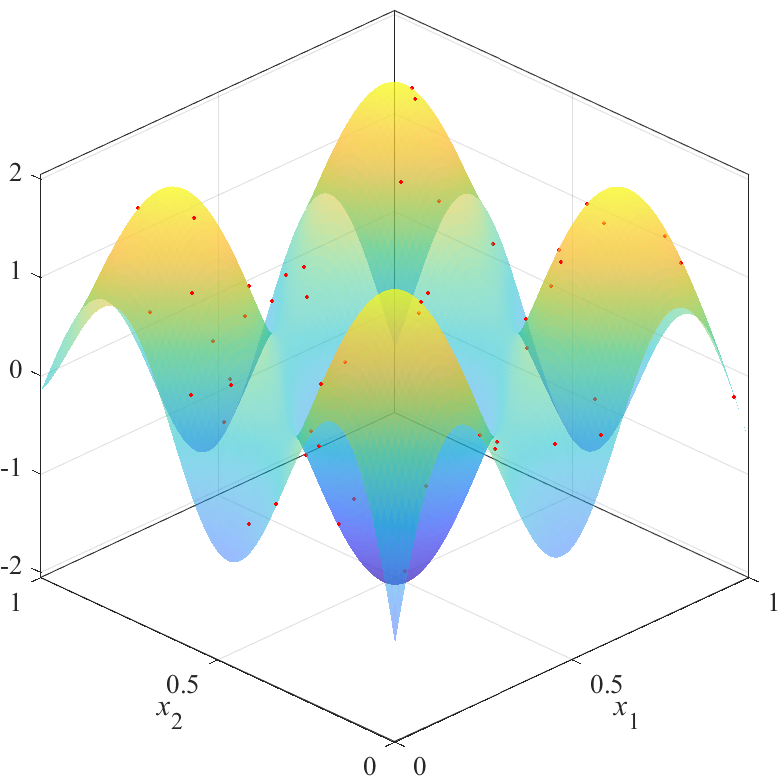
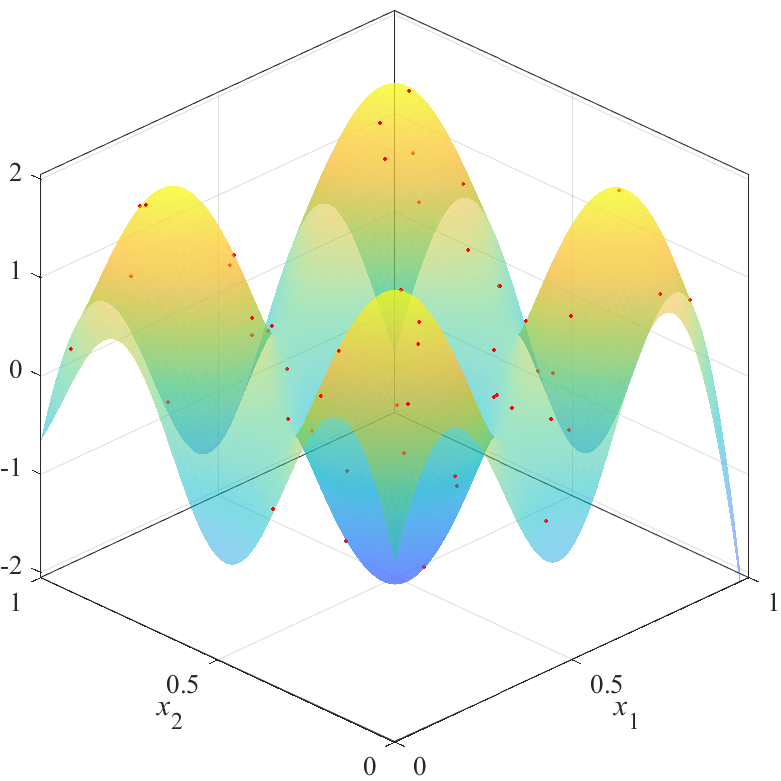
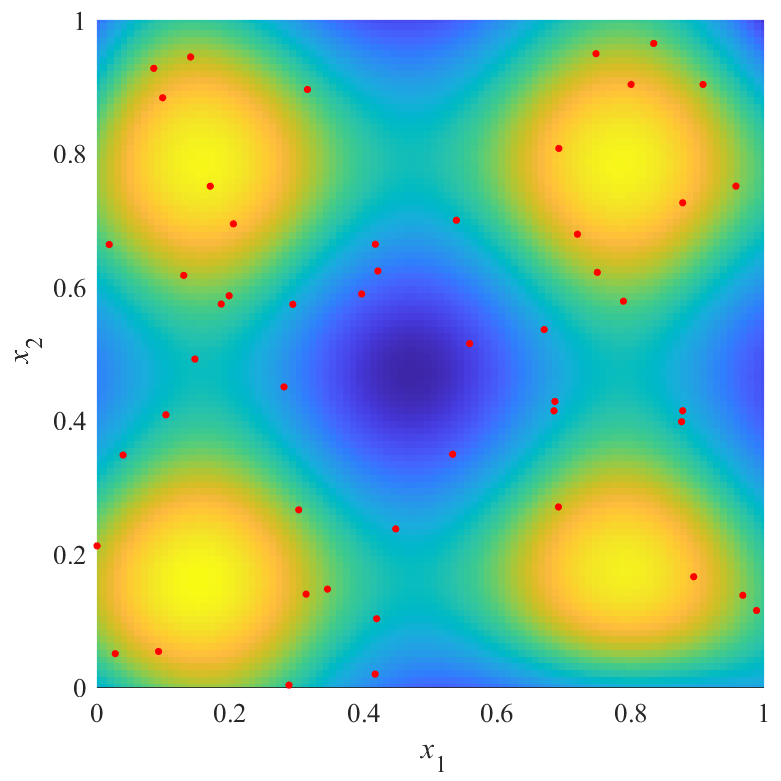
図の赤点が点群X，青から黄色の面が推定した応答曲面を表します．
上の図は，斜めから見た図で，曲面の高さと色で推定結果を表しています．
曲面は透明度0.5でプロットされており，重なり合っている部分は色が濃くなっています．
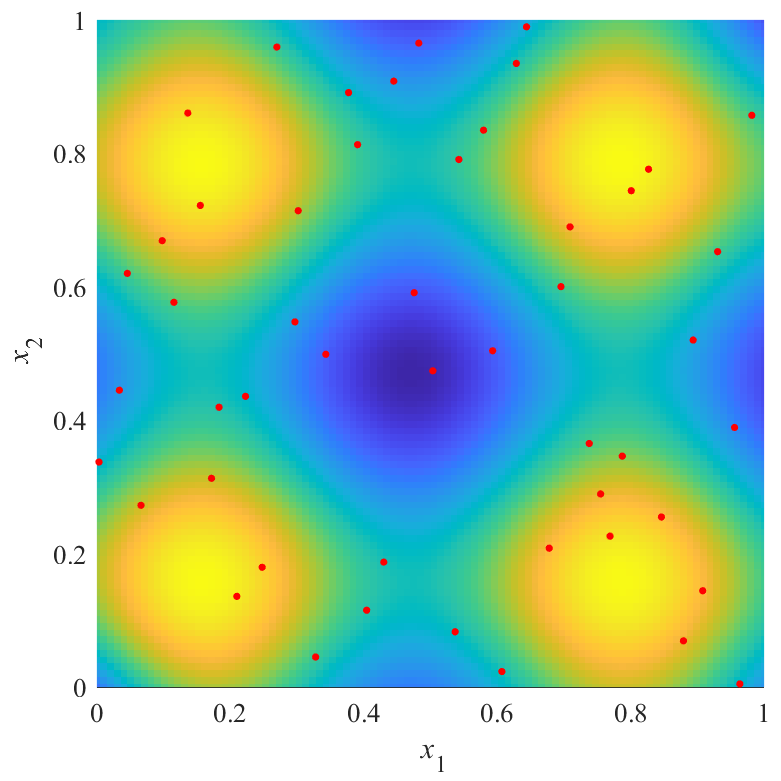
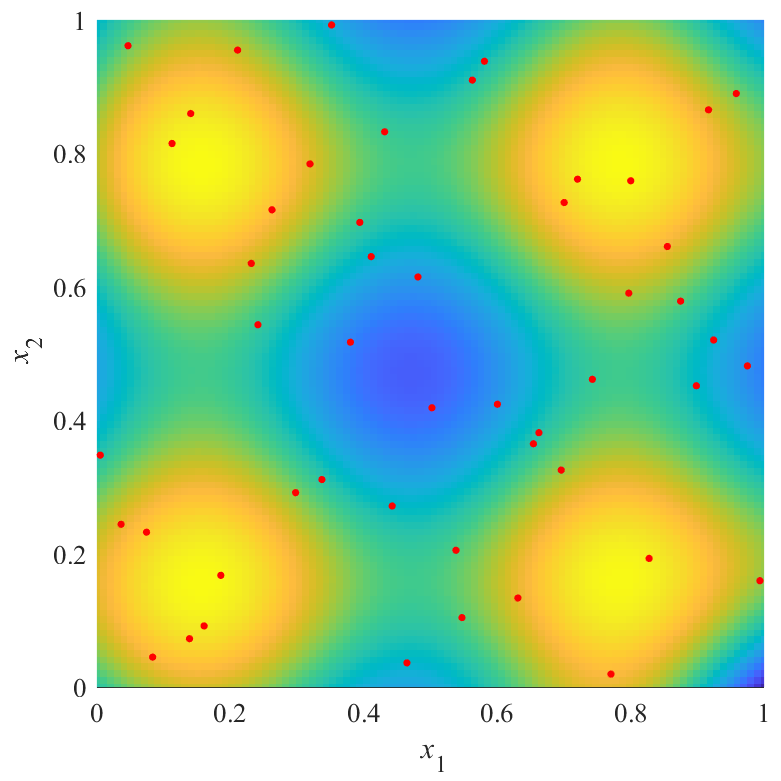
下の図は，同じものを真上から見た図で，色で推定結果を表しています．

図から，評価値が最も良いX2は，$x_1=x_2$を軸とした左右対象に近い結果を得られることが分かります．
逆に，評価値が最も悪いX3は，左右非対象な結果を得られていることが分かります．
また，X2の結果とX3の結果にも大きな差があることが分かります．

一般に，乱数を含む結果には振れがあるため，1試行の結果だけで結論を出すことができません．
そこで，点群サイズを20～100に変化させて，各サイズ101試行した推定結果を確認します．

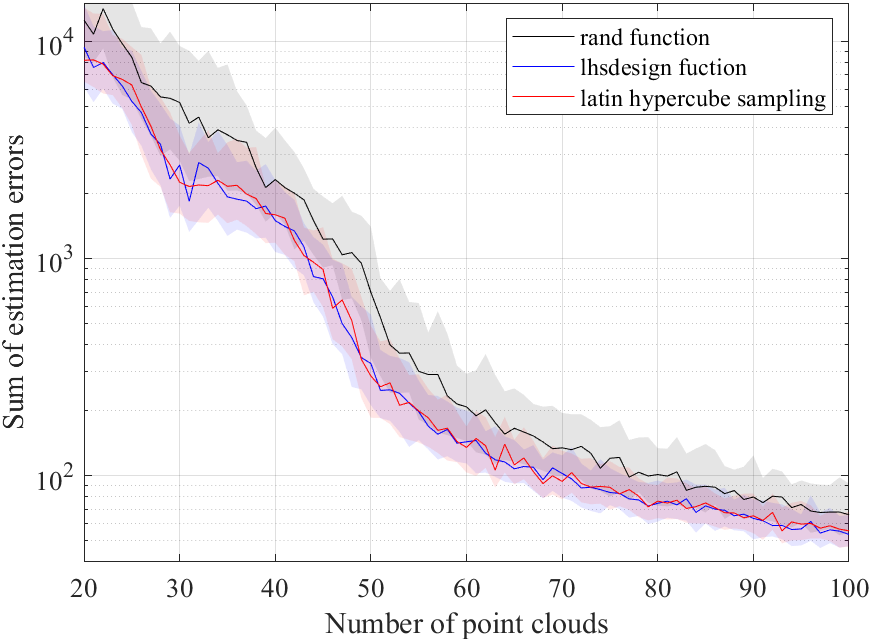
上の図は，横軸が点群サイズ，縦軸が評価値です．縦軸はログスケールです．
黒，赤，青の各色がX1，X2，X3の結果に対応します．
濃い線は中央値の結果，その周辺の薄く色のついた領域は四分位範囲を表します．
図から，点群サイズが大きくなるほど推定精度，評価値が良くなることが分かります．
Random samplingよりLHSを利用した方が，構築した推定モデルの精度が良いことが確認できます．
また，X2とX3の推定精度が同程度であることが確認できます．

点群から推定した曲面（ガウス過程回帰）

RBNNと同様に，ガウス過程回帰でも推定をしてみます．
MATLAの組み込み関数fitrgpとpredictを利用した，次式で点群Yの高さを推定します．

  EH = predict(fitrgp(X,XH),Y); % 点群Yの高さ（推定値）

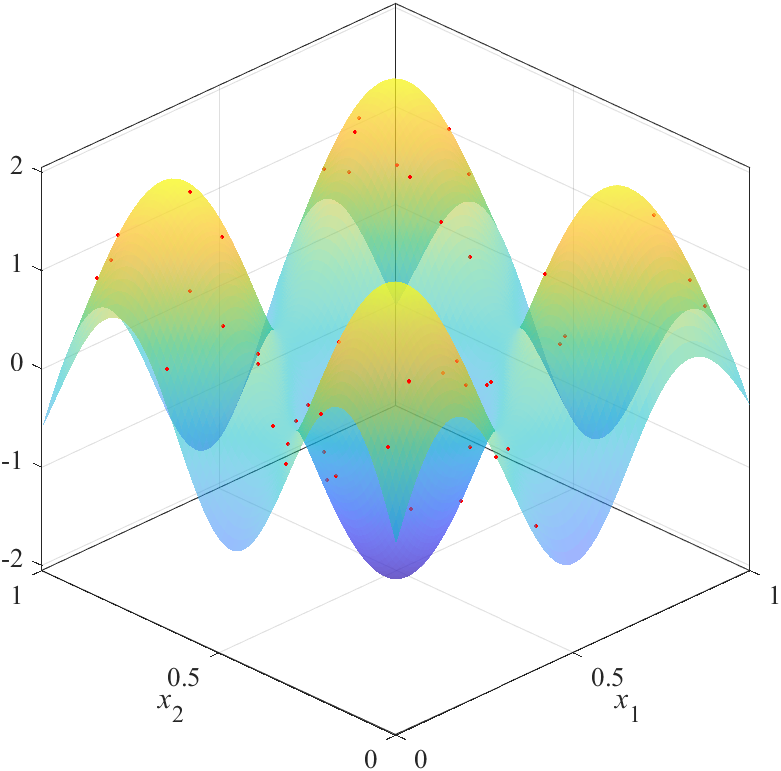
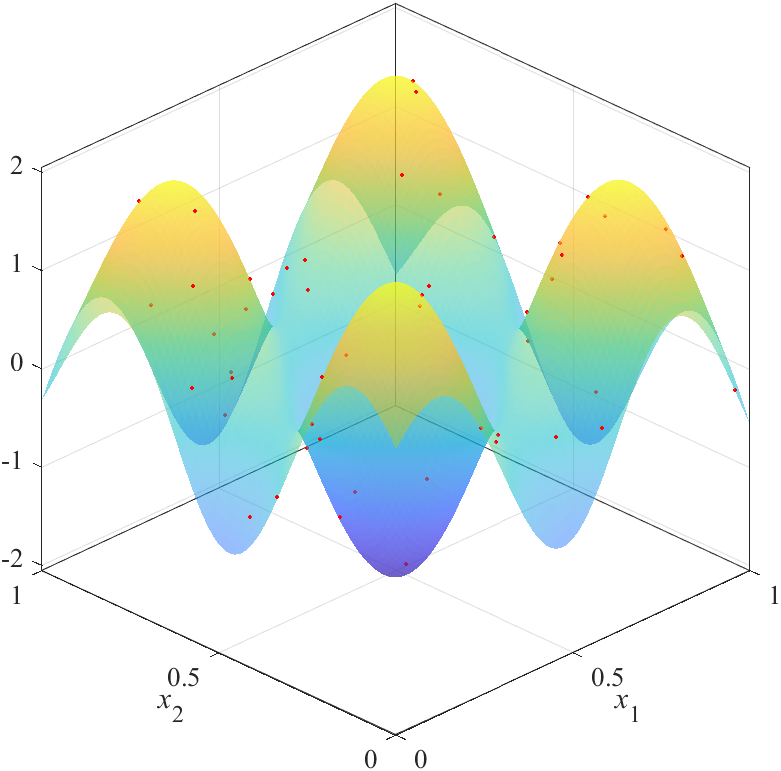
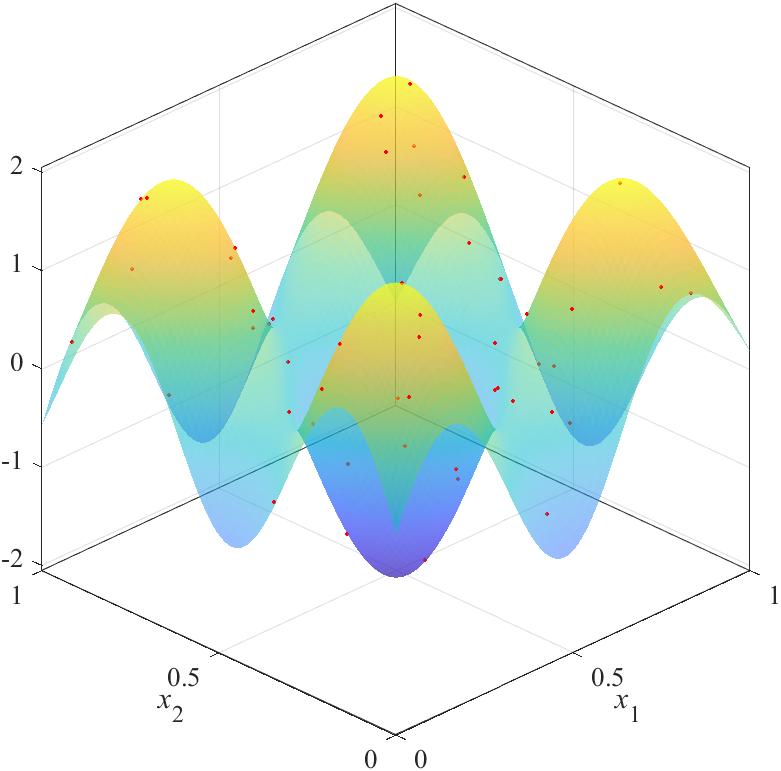
推定した応答曲面と誤差（真値と推定値の差）の合計は，以下になります．


X1: 374.5022	X2: 274.8412	X3: 272.5964

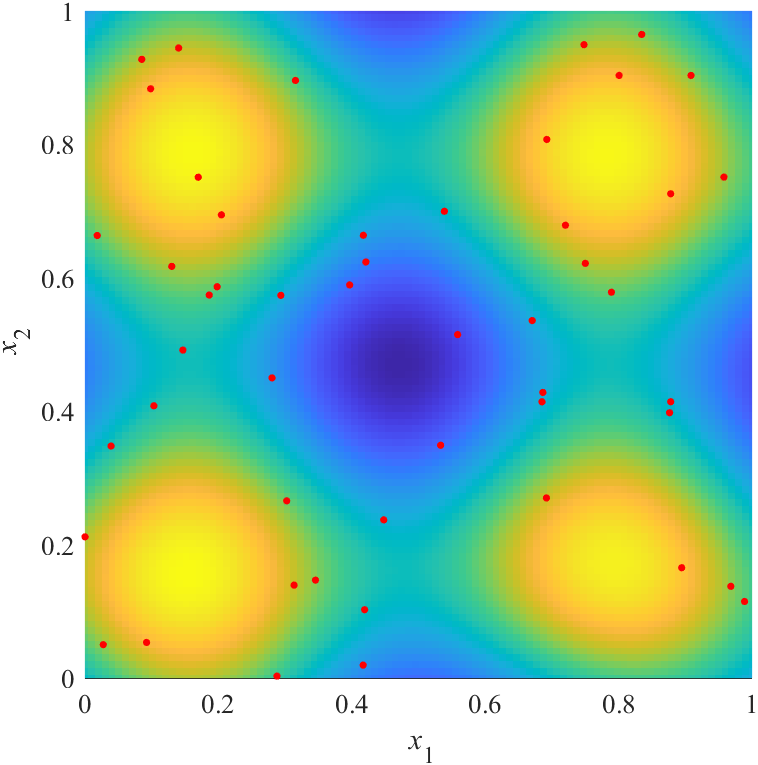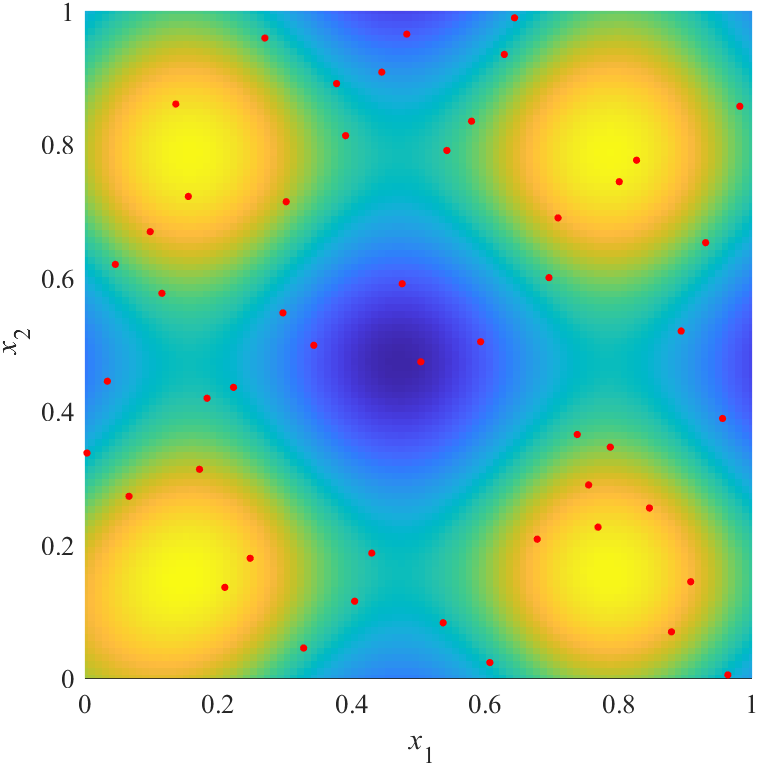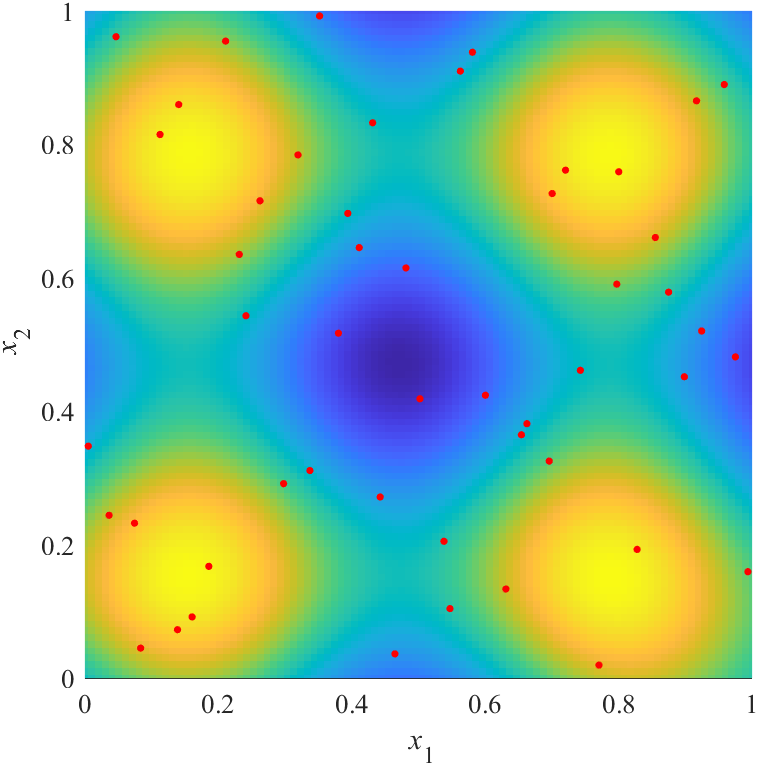点群サイズを20～100に変化させて，各サイズ101試行した推定結果は，以下になります．

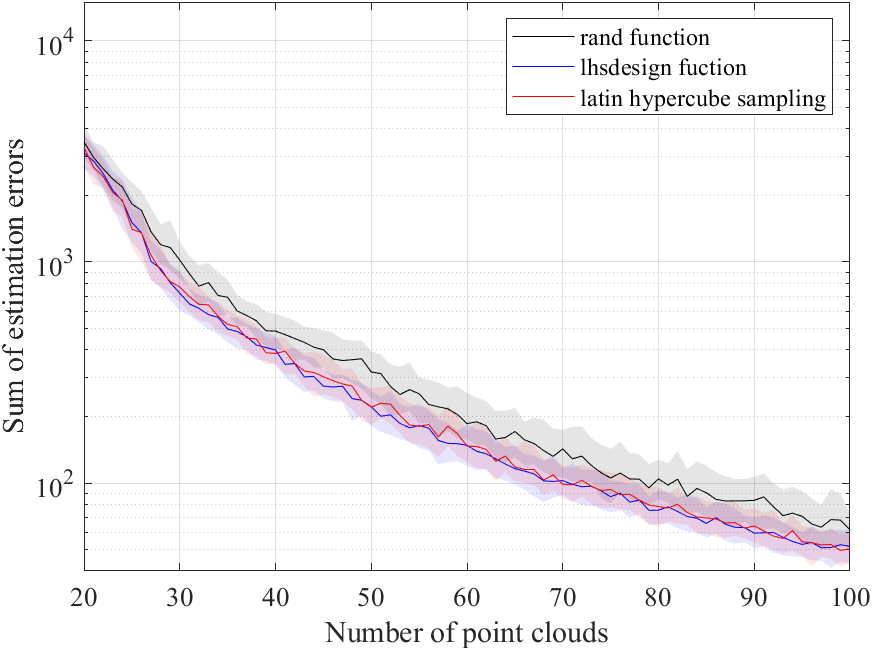
応答曲面法がガウス過程回帰の場合でもRandom samplingよりLHSを利用した方が，構築した推定モデルの精度が良いことが確認できます．

終わりに

この記事では，LHSによって生成される点群の性質と効果を視覚的，数値的に見てきました．
視覚的に分かり易い2次元の結果に焦点を当てましたが，2次元以外でも同様の結果が得られるはずです．
もし興味があれば，以下のような変更を加えて自分で実験してみると，より理解が深まると思います．

点群サイズ$N$，次元数$D$，乱数シード，試行数といった数値パラメータを変更する
乱数発生器やサンプリング元の分布を変更する
乱数をSobol, Haltonなど別のものに変更する
応答曲面法を多項式近似，サロゲート加重平均など別のものに変更する
結果に有意差があるか検定する