LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@tomtkg

AHC043参加記

Posted at

RECRUIT 日本橋ハーフマラソン 2025冬（AtCoder Heuristic Contest 043）に参加しました．
最終順位は，255 / 1422でした．AHC043参加の記録をここに残します．

問題理解～サンプル実行

問題理解

最初は問題の理解に努めます．箇条書きで，理解した内容をメモとして残します．

  • 環境：$50\times50$の2次元グリッド
  • 目的：所持金の最大化
  • 出力：$T=800$ターンの行動
    • 座標($i,j$)に線路を建設，所持金-100
    • 座標($i,j$)に駅を建設，所持金-5000
    • 待機，所持金±0
  • 入力
    • 初期資金$K$(=11000~20000)
    • $M$(=50~1600)人の家と職場の座標

簡単な例による理解

※この記事では，すべての距離はマンハッタン距離で考えます

次は，非常に簡単な例をシミュレーションします．

距離が$d$離れた2地点$\boldsymbol{a}$と$\boldsymbol{b}$を考えます．
$\boldsymbol{a}$と$\boldsymbol{b}$は，ある人の家と職場とします．
$\boldsymbol{a}$と$\boldsymbol{b}$に駅を建設し，その間に線路を建設する場合，

  • 建設に必要なターン数：$d+1$
  • 建設に必要な資金：$9900+100\times d$
  • 最初に建設可能な最大距離$d_{max}$：$11$~$101$　（$98$がグリッドのmax）
  • 資金回収に必要なターン数$x$（1人を輸送する場合）：
    • $9900+100\times d = d \times x \Rightarrow x = 100 + \frac{9900}{d}$

となります．駅と線路の建設後は，毎ターン，資金が$d$増加します．

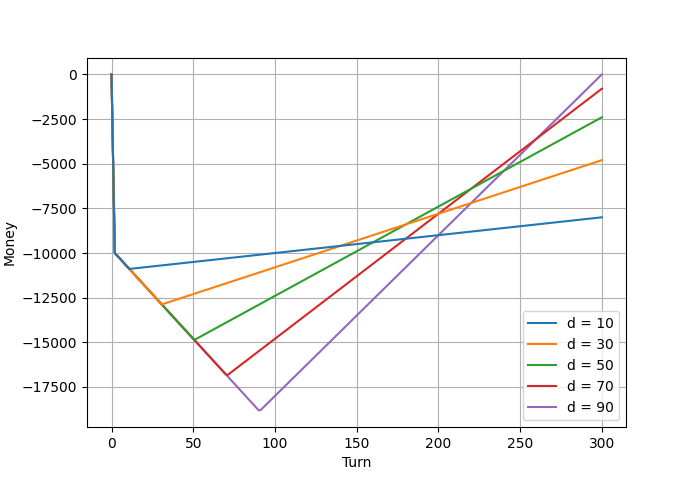
2地点間の距離$d=\{{10,30,50,70,90\}}$を考えます．
ターン経過による資金の変動は，以下になります．

Figure_1.png

収入が距離$d$に依存していること，線路建設と比較して駅建設の費用が非常に大きいことから，なるべく$d$が長くなるような2地点に駅を建設するのが良いとわかります．

$d=90$の場合，300ターン目に建設資金が回収できます．
（建設ターン：91，建設資金：18900，資金回収ターン：210）
一方，$d=10$の場合，800ターンが終了しても建設資金が回収できません．

少し複雑な例による検討

次は，先ほどの例において，複数人を輸送できるケースを考えます．
多人数をなるべく長距離輸送するのがベストですが，
1人を長距離輸送するのと複数人を短距離輸送するのは，どちらが良いでしょうか．

これは，800ターン終了時点での最終的な所持金を比較するのがベストでしょう．
最終的な所持金$s$は，以下の式で導出できます．$$
s = K - (9900 + 100\times d) + (800 - d)\times \Sigma_{i=1}^n d_i
$$ここで，$K$は初期資金，$d$は駅間の距離，$n$は輸送人数です．
また，$d_i$は$i$さんの家から職場までの距離です．
簡単にするため，$d_i=d$として計算すると，
$(K,d,n)=(0,90,1) \Rightarrow s=45000$，
$(K,d,n)=(0,38,2) \Rightarrow s=45558$，
$(K,d,n)=(0,25,3) \Rightarrow s=45725$です．

距離が短くても複数人を輸送した方が有利になるケースが多いことが確認できます．
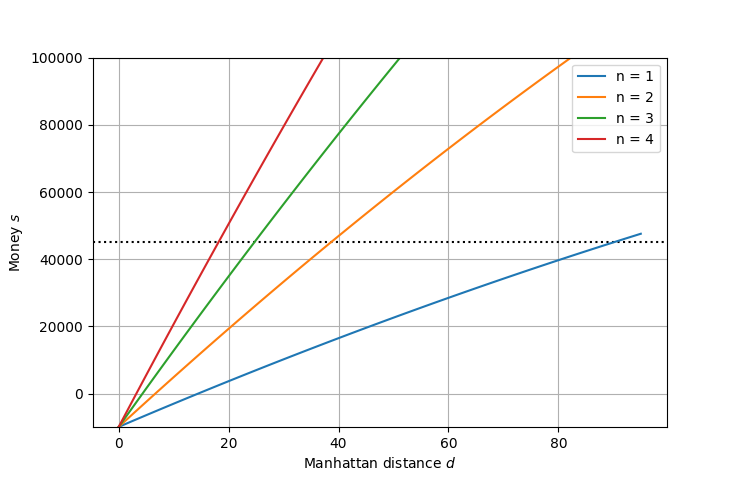
輸送人数$n=\{{1,2,3,4\}}$における距離$d$と最終的な所持金$s$の関係は，以下になります．

Figure_2.png

$s=45000$の地点に水平線を引いています．
距離$d=0$の場合，駅建設の費用のみ発生し，収入は0のため，$s=-10000$になります．
多人数を長距離輸送しているほど，最終的な所持金$s$が大きくなることが確認できます．

サンプル実行

次は，提供されているPythonによるサンプルプログラムを実行します．
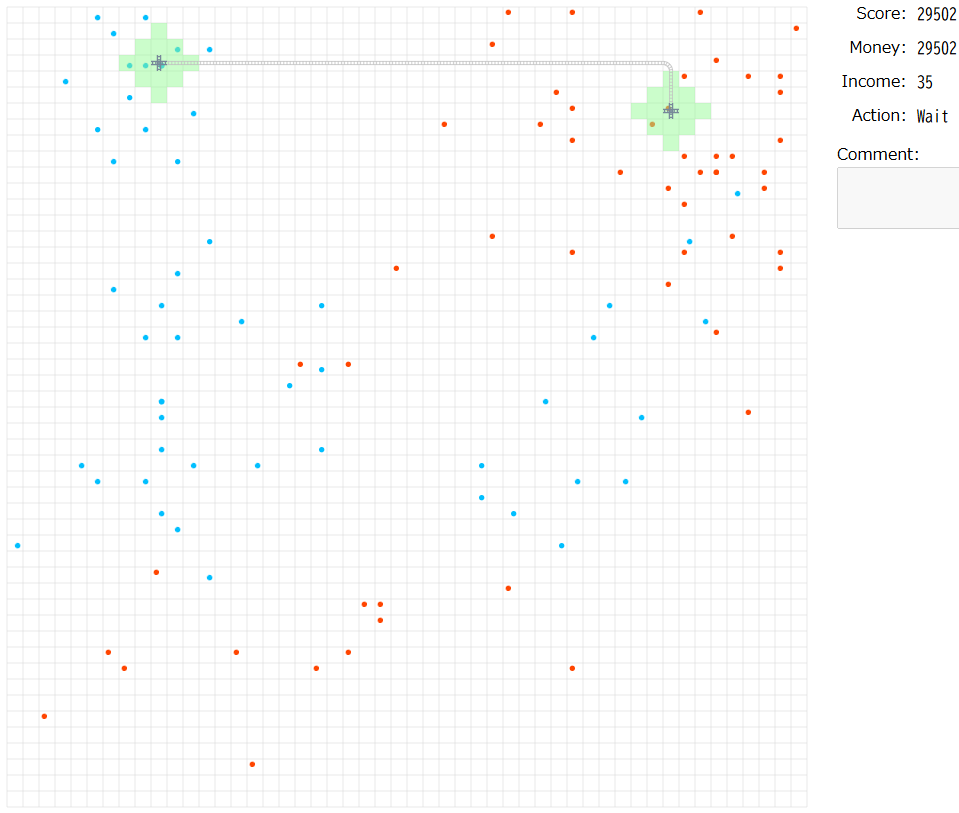
224行のプログラムを実行すると，score=29502が画面に表示されました．
また，Visualizerに出力を張り付けると，以下のようになりました．

image.png

$(K,d,n)=(16127,35,1)$のプログラムが実行され，$s=29502$がスコアになっていることが確認できました．

サンプル理解～最初の解法の提出（2駅建設）

サンプルの理解と方針の決定

サンプルプログラムには色々な処理が書かれていますが，AHC競技者に重要なのは，solver.solve()の中身です．

solver.solve()の中身は，以下の4つに分けられます．

  1. 人0，人1，... と順に見て，家と職場の位置に駅を配置したとき，駅の間を最短距離で線路接続可能な人を見つける（初期資金$K$の範囲内で）
  2. 見つけた人の家と職場の位置に駅を配置する
  3. 2つの駅の間を接続する線路を配置する
  4. その後は$T$ターン目まで待機する

最初の解法として，1. と 2. を以下のように変更してみます．
（初期資金$K$の範囲内で）最終的な所持金$s$が最も大きく2地点を見つけ，そこに駅を配置する

この実装のためには，人を順に見るのではなく，2次元グリッドを精査する必要があります．
そして，任意の2地点$(x_1,y_1)$，$(x_2,y_2)$を駅に選んだ場合，何人輸送できるか分かる必要があります．
今回は，セルの数$=50\times50=2500$に対して，人の数$M$が少ないため，家と職場の周りのみ探索します．

実装1（2駅建設）

まず，任意の地点に駅を配置した時，誰の自宅 / 誰の職場が駅の圏内に含まれるか直ぐにわかるようにします．
プログラムは，以下になります．

build_map
OFFSETS = [(0, 0),
    (1, 0), (-1, 0), (0, 1), (0, -1),
    (1, 1), (1, -1), (-1, 1), (-1, -1),
    (2, 0), (-2, 0), (0, 2), (0, -2),
]

def build_map(points: list[Pos], N: int) -> dict[Pos, set[int]]:
    m = {}
    for i, (px, py) in enumerate(points):
        for dx, dy in OFFSETS:
            x, y = px + dx, py + dy
            if 0 <= x < N and 0 <= y < N:
                m.setdefault((x, y), set()).add(i)

    return m
Solver.__init__
self.home_map = build_map(home, N)
self.work_map = build_map(workplace, N)

これで，準備完了です．
そして，solver.solveを以下のように書き換えます．

main1.py
def solve(self) -> Result:
    # 接続する人を見つける
-   rail_count = (self.K - COST_STATION * 2) // COST_RAIL
-   person_idx = 0
-   while person_idx < self.M:
-       if distance(self.home[person_idx], self.workplace[person_idx]) - 1 <= rail_count:
-           break
-       person_idx += 1
-   assert person_idx != self.M
+
+   max_d = (self.K - COST_STATION * 2) // COST_RAIL + 1
+   score = 0
+   st1, st2 = None, None
+   
+   for p1, h_ids in self.home_map.items():
+       for p2, w_ids in self.work_map.items():
+           d = distance(p1, p2)
+           if d < 5 or max_d < d:
+               continue
+           
+           pair_ids = h_ids & w_ids
+           if p2 in self.home_map and p1 in self.work_map:
+               pair_ids |= self.home_map[p2] & self.work_map[p1]
+               
+           income = sum(distance(self.home[id], self.workplace[id]) for id in pair_ids)
+           s = self.K - (9900 + 100 * d) + (800 - d) * income
+           
+           if s > score:
+               score = s
+               st1, st2 = p1, p2

    # 駅の配置
-   self.build_station(*self.home[person_idx])
-   self.build_station(*self.workplace[person_idx])
+   self.build_station(*st1)
+   self.build_station(*st2)

2次元グリッドの全域ではなく，家と職場の周りのみ探索します．
まず，2地点間の距離$d$を求め，初期費用で駅と線路を建設可能であることを確認します．
また，距離$d$が一定以上大きい値であることを確認します．
次に，駅2つと線路を建設した場合の最終的な所持金$s$を計算します．
そして，$s$が最大となる2地点を求め，st1，st2とします．
その後の線路を配置する操作と$T$ターン目まで待機する操作は，変更しません．

この最初の解法について，seed=0では以下の結果が得られました．

image.png

結果は，$(K,d,n)=(16127,43,2)$，$d_1=44$，$d_2=47$，$s=70814$でした．
ただし，このプログラムを提出したところ，幾つかのケースで実行時間制限を超過しました．

実装2（2駅建設，データ制限）

実行時間制限を超過しているため，プログラムを高速化する必要があります．
seed=0での結果を分析しながら，プログラムを改変します．

まず，build_mapの2重のfor loopを考えます．

for i, (px, py) in enumerate(points):
    for dx, dy in OFFSETS:

このfor loopによって，$54\times13=702$回，内部処理が実行されていました．
pointsの最大サイズは1600ですが，OFFSETSのサイズは13で固定です．
内部処理も軽いため，この処理は変更不要と判断しました．

次に，solver.solve()の2重のfor loopを考えます．

for p1, h_ids in self.home_map.items():
    for p2, w_ids in self.work_map.items():

このfor loopによって，$475\times490=232750$回，内部処理が実行されていました．
マップの最大値は$50\times50=2500$なので，最大で$2500\times2500$回，内部処理が実行される可能性があります．
これがプログラムが遅い原因と判断し，for loopの回数を$3000\times300=90000$までに制限します．
関数build_mapの末尾に以下を追加しました．

build_map
def build_map(points: list[Pos], N: int) -> dict[Pos, set[int]]:
    m = {}
    ...
    
+   m = dict(sorted(m.items(), key=lambda item: len(item[1]), reverse=True)[:300])
    return m

この変更によって，家や職場が密集している上位300地点の情報のみが保持されます．
他の家，他の職場が周りに存在しない地点は，探索されない可能性が生じます．

プログラムを変更をしても，プログラムの出力は変化しませんでした．
このプログラムを提出したところ，無事，結果が受理されました．
得点は4248691で，提出時点での順位は330位でした．

3駅建設への対応

実装3（3駅建設）

より所持金$s$を大きくするため，駅を複数建設し，それらを線路で繋ぐことを考えます．
まずは，先ほどの方法で駅を2つ建設した後，駅を1つ追加して，既存駅に接続します．
追加する駅をマップ全体から探索することは，実行時間の観点から現実的ではありません．
そこで，追加する駅の位置は，建設済みの駅の情報を活用して決定します．

具体的には，建設済みの駅から，その駅を利用可能な家 / 職場を持つ人の集合を得ます．
そして，それらの人の対応する職場 / 家の周囲を探索し，評価$v$の高い場所に駅を建設します．
場所の評価$v$は，最終的に以下の式を採用しました．
$$
v = 1000\times n + 10\times\Sigma_{i=1}^n d_i + 周辺の家の数 + 周辺の職場の数
$$ここで，$n$は輸送人数，$d_i$は$i$さんの家から職場までの距離＝１ターン毎に$i$さんから得られる収益です．
多人数の輸送を第1優先，１ターンの収益最大化を第2優先とし，駅を利用可能な周辺の家 / 職場の数も考慮しています．
最後の項目は，駅を複数建設することを見越した，将来の収益最大化を考えた設定です．
所持金の正確な見積もりは困難と判断し，上記の式で，駅の建設候補地を評価します．

駅の建設候補地は，以下のプログラムで求めます．

get_ids
def get_ids(stations: list[Pos], map: dict[Pos, set[int]]) -> set[int]:
    ids = set()
    for p in stations:
        if p in map:
            ids |= map[p]
    return ids
main3.py
home_ids = get_ids(stations, self.home_map)
work_ids = get_ids(stations, self.work_map)

candidate = []
candidate.extend(self.workplace[id] for id in (home_ids - work_ids))
candidate.extend(self.home[id] for id in (work_ids - home_ids)

for x, y in candidate:
    for dx, dy in OFFSETS:
    ...

実装1で用意したself.home_mapとself.work_mapを活用する関数get_idsを作成します．
get_idsに建設した駅のリストstationsとマップを入力し，対応する家 / 職場持つ人の集合を得ます．
そして，人の集合から家 / 職場の位置を求め，駅の建設候補地とします．
駅の建設候補地の周辺を確認し，評価$v$が最も高い箇所に駅を建設します．

実装3では，最終的に以下の結果が得られました．

image.png

1ターンの収益が$91\Rightarrow 141$となり，最終的な所持金も$70814\Rightarrow 97764$となりました．
ちなみに，線路建設の処理はサンプルを複製したのですが，最初はエラーが出ました．
線路の始点と終点を入れ替えたところ，上記の結果が得られました．

実装4（建設済み線路対応）

線路建設の処理に問題があることがわかったので，修正します．
新しい線路建設アルゴリズムは，以下の方針で実装をします．
[1]. 駅から垂直に移動した後，直角に曲がり，水平に移動する経路を試す
　　駅に到達 ⇒ [4]へ　　　　線路に到達 ⇒ [2]へ　
[2]. 駅から水平に移動した後，直角に曲がり，垂直に移動する経路を試す
　　駅に到達 ⇒ [4]へ　　　　線路に到達 ⇒ [3]へ　
[3]. [1] [2]のうち短い経路を採用し，経路が到達した線路に駅を建設し，[4]へ
[4]. 経路上に線路を建設

この方針の場合，経路を試す処理と実際に線路を建設する処理をわける必要があります．
経路は，[(1, 3), (1, 4), (2, 4)]のように，list形式で位置座標を持つことにします．

線路を建設するプログラムは，以下になります．

get_symbol
def get_symbol(prev: Pos, curr: Pos, next: Pos) -> int:
    if prev[0] == next[0]: return 1  # RAIL_HORIZONTAL
    if prev[1] == next[1]: return 2  # RAIL_VERTICAL

    if prev[0] < curr[0] and curr[1] < next[1]: return 5  # RAIL_RIGHT_UP
    if prev[0] < curr[0] and curr[1] > next[1]: return 4  # RAIL_LEFT_UP
    if prev[0] > curr[0] and curr[1] < next[1]: return 6  # RAIL_RIGHT_DOWN
    if prev[0] > curr[0] and curr[1] > next[1]: return 3  # RAIL_LEFT_DOWN

    if prev[1] < curr[1] and curr[0] < next[0]: return 3  # RAIL_LEFT_DOWN
    if prev[1] < curr[1] and curr[0] > next[0]: return 4  # RAIL_LEFT_UP
    if prev[1] > curr[1] and curr[0] < next[0]: return 6  # RAIL_RIGHT_DOWN
    if prev[1] > curr[1] and curr[0] > next[0]: return 5  # RAIL_RIGHT_UP
Solver.build_rails
def build_rails(self, path: list[Pos]) -> None:
    for i in range(1, len(path) - 1):
        symbol = get_symbol(path[i - 1], path[i], path[i + 1])
        self.build_rail(symbol, path[i][0], path[i][1])

get_symbolは，連続する3つの位置座標から，建設する線路の形状を求める関数です．
単純だが面倒な処理は，この関数に押し込みました．
pathは，経路の情報を持つ変数です．
その最初と末尾の要素は，駅の位置座標を表します．
build_railsは，2つの駅間に線路を建設する関数です．
変数pathを受け取り，その情報を基にself.build_railをlen(path)-2回呼び出します．
self.build_railは，サンプルに書かれている線路建設関数です．

経路を試すプログラムは，以下になります

next_position
def next_position(flag: bool, p: Pos, target: Pos) -> Pos:
    r, c = p
    tr, tc = target
    if (flag and c != tc) or (not flag and r == tr):
        c += (tc > c) - (tc < c)  # cをtargetに近づける
    else:
        r += (tr > r) - (tr < r)  # rをtargetに近づける
    return r, c
Solver.build_next
def build_next(self, stations: list[Pos], station: Pos) -> list[Pos]:
    target = min(stations, key=lambda x: distance(x, station))
    flag = False
    path, path2 = [station], [station]

    while True:
        p = path[-1]

        if p == target:  # 駅に到達
            self.build_rails(path)
            self.build_station(*station)
            return stations + [station]

        if self.field.rail[p[0]][p[1]] != EMPTY:  # 建設物に到達
            if flag:  # [1][2]に失敗
                break
            else:  # [1]に失敗
                flag = True
                path, path2 = path2, path

        path.append(next_position(False, p, target))

    path = min(path, path2, key=len)
    self.build_station(*path[-1])
    self.build_rails(path)
    self.build_station(*station)

    return stations + [path[-1], station]

関数next_positionは，flag=Falseの場合，垂直優先で経路を探索します．
逆にflag=Trueの場合，水平優先で経路を探索します．

build_nextは，経路を試す過程を含む関数です．
建設済みの駅のリストstationsと建設したい駅stationを入力として受け取り，内部で線路と駅を建設し，更新したstationsを出力します．
最初に垂直優先で経路を探索し，探索に失敗した場合はflag を変更し，水平優先で経路を探索します．

以上の実装で，プログラムのエラー終了が無くなりました．
本質的ではないので省略していますが，お金に関する処理は，build_railとbuild_station，build_nothing内に記載しています．

n駅建設への対応（反省会）

ここから，迷走しました．
迷走した内容，最後まで分からなかった部分を記録として残します．

  • 駅を建設する地点を2つ決めた後の行動
    • 駅を建設したい地点を先に決めるべきだった？
      • 効率的に最初の線路建設をできるが，駅建設の柔軟性が無くなる
    • すぐに駅と線路を建設するべきだった？
      • 最適な位置に次の駅を建設できるが，線路の位置取りが悪い可能性
  • 駅を建設する地点の探索範囲
    • $N\times N$のグリッドを全探索 ⇒ 最適だが，時間的に不可能
    • 家と職場の周囲に限定した全探索 ⇒ 最適だが，時間的に不可能
    • 分布に従う確率的な探索が良かった？
    • なるべく多くの家と職場をカバーする位置を抽出 ⇒ 採用
      • 時間制限はクリアできるが，最適性が犠牲になっている
  • 駅を建設する地点の選び方
    • 1駅建設した時点での利益最大化で良いのか？
    • 2駅の建設を同時に考えた方が良いのか ⇒ 難しさ
    • 最終的な利益の最大化を考えたとき，最適な評価基準は何か？
    • 線路と駅を建設しながら，次の駅建設地点を選ぶべきなのか？
    • 単純な線路を仮定したうえで，駅建設地点をどんどん選ぶべきなのか？
  • 建設の終了条件
    • ターン数で決め打ち ⇒ 良くない
    • 評価が下がった時 ⇒ 良くない
      • 1駅建設して評価が下がっても，さらに追加で駅を建設すると最終スコアがプラスになるケースが多くあった
    • 評価がプラスになる，駅の建設候補地点が無くなった時 ⇒ 採用
      • 候補地点の数に依存するが，ベターな選択と判断
  • その他
    • プログラムの途中で駅建設の方針などを切り替えるべきだった？
    • 建設した線路や駅の情報をもっとかつようするべきだった？
    • ターン数やプログラム実行時間に応じて動的に処理を変える必要があった？
    • 言語はPythonで良かった？（上位はC++ばかり）
    • エラーの効率的な見つけ方，直し方がわからない
    • 実行時間の効率な使い方がわからない（chokudaiサーチ以外にもある？）

終わりに

不甲斐ない順位となってしまい，残念でした．
より良い結果を出すために自分に足りない部分がわかったので，その理解を深めて技能を習得していきたいと思います

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?