Diffusion Models are Evolutionary Algorithmsという論文（arXivに投稿されたプレプリント)を読みました．論文タイトルは「拡散モデルは進化アルゴリズムである」と訳せます．
論文内容の紹介・解説は他の方にお任せするとして，この記事では論文で提案された「拡散進化アルゴリズム（Diffusion Evolution algorithm）」を検証（再現）します．
著者によるプログラムが以下に公開されています．（公開1か月で⭐100+）
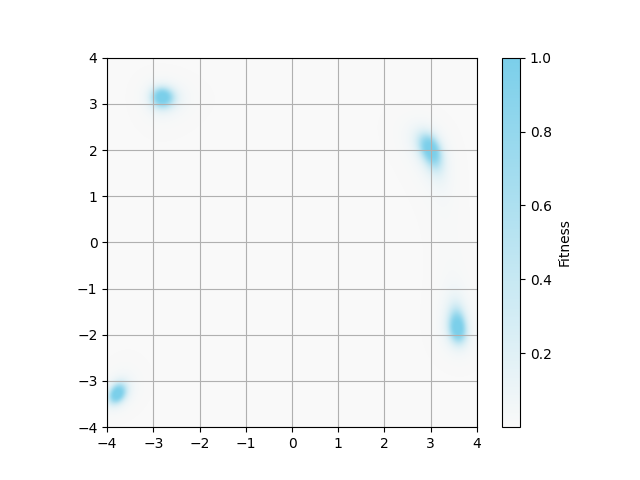
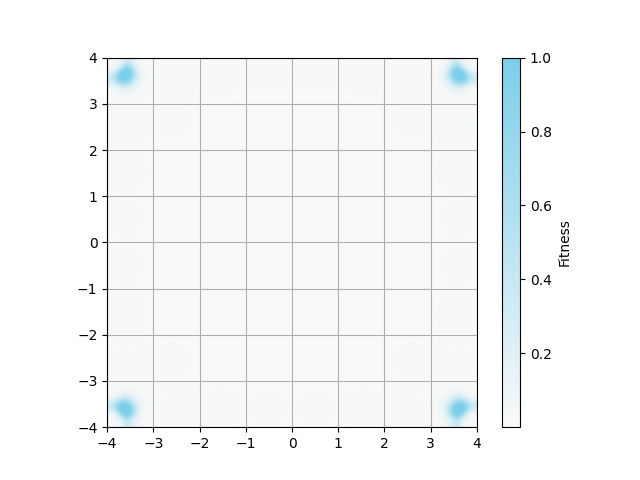
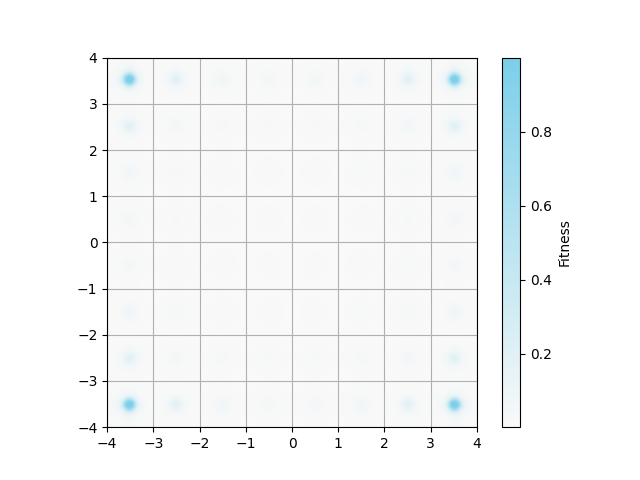
図1について
以下のコマンドで図1の解集合を出力できました．
git clone https://github.com/Zhangyanbo/diffusion-evolution diffevo
cd diffevo
pip install .
cd experiments/2d_models/two_peaks
python diffusion.py
コードを見ると，図1は512個の解をfitnessで色付けして描画しています．
3つの画像は，それぞれ0, 80, 98世代（反復回数）での解集合を描画しています．
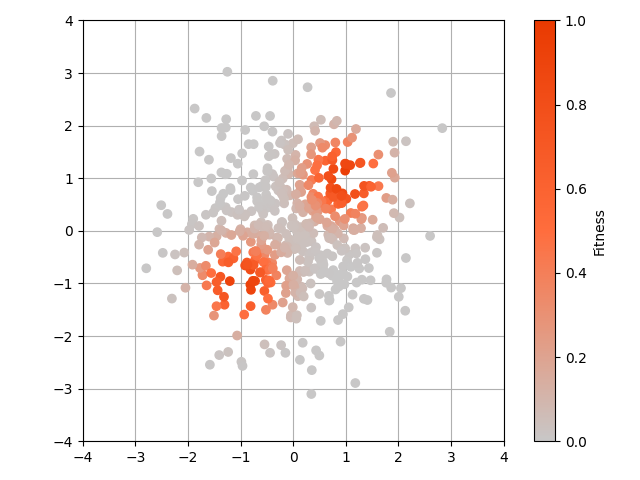
0世代は，x0 = torch.randn(num_population, 2)で生成されたランダムな初期解集合です．
コードの一部を変更して軸などを追加すると，以下の画像が得られました．
 |
 |
|---|---|
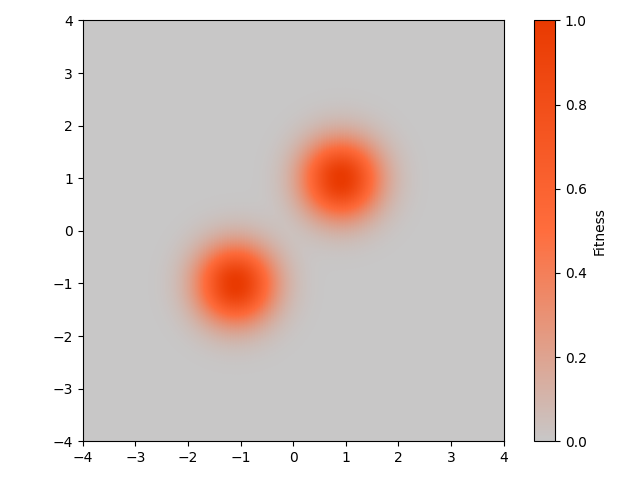
| 関数の景観 | $\mathrm{x}_T$（0世代目） |
 |
 |
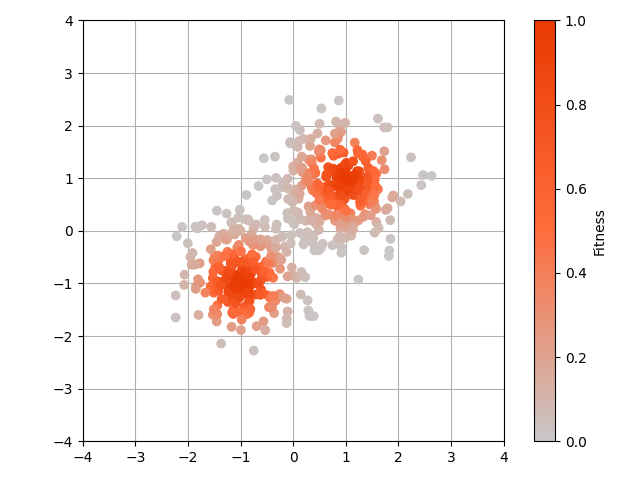
| $\mathrm{x}_t$（79世代目） | $\mathrm{x}_{t-1}$（80世代目） |
 |
 |
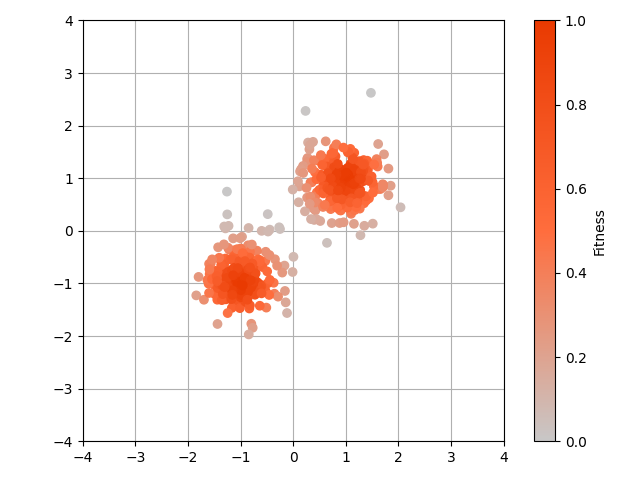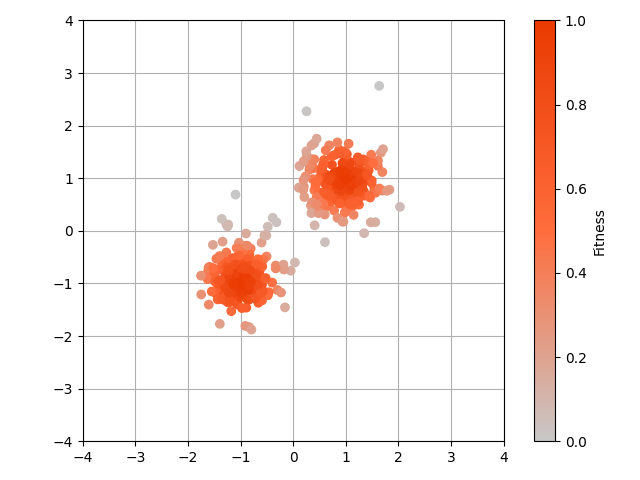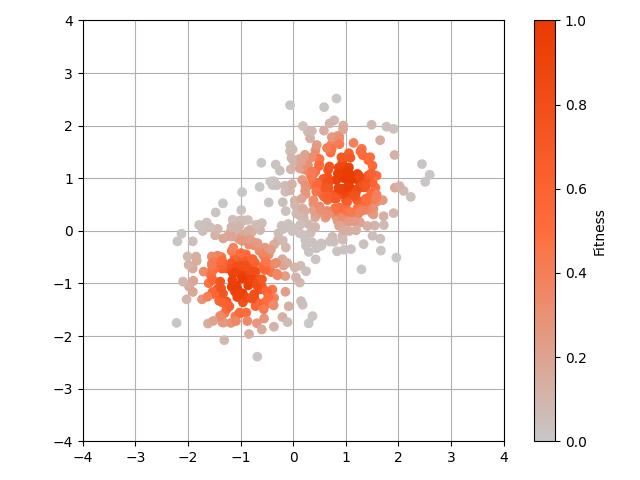
| $\mathrm{x}_1$（97世代目） | $\mathrm{x}_0$（98世代目） |
$(x_1,x_2)=(1,1)$を中心とする正規分布と$(x_1,x_2)=(-1,-1)$を中心とする正規分布を足し合わせて，関数（2変数の最大化問題）を作成しています．
論文では，1世代が経過すると$\mathrm{x}$の添え字が1減少する書き方をしています．
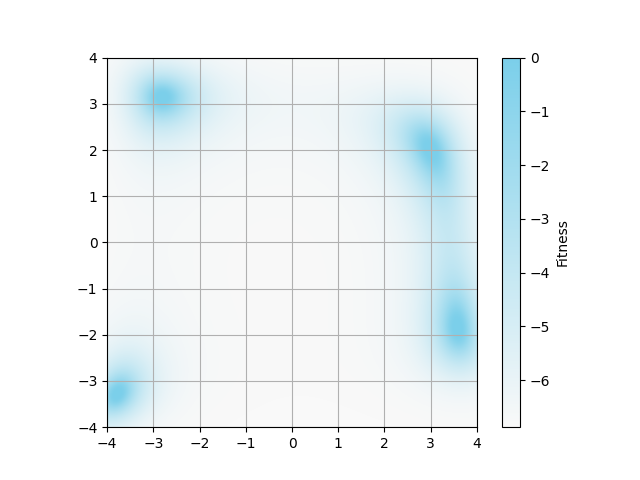
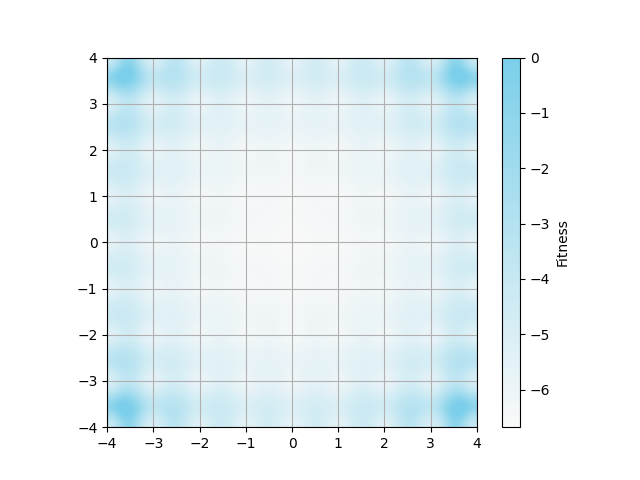
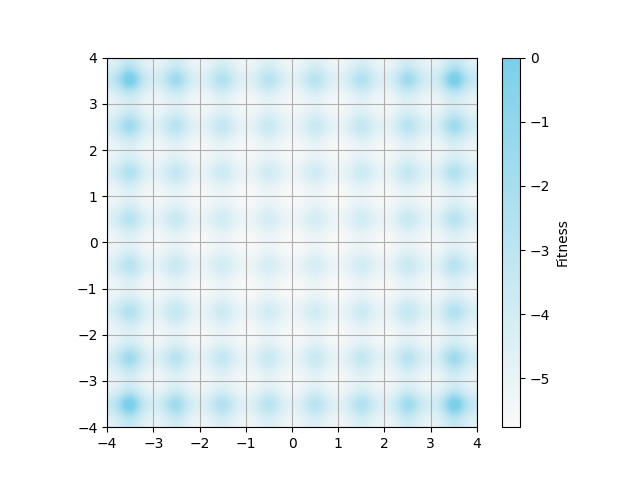
図2について
以下のコマンドで図2を出力できました．
cd experiments/2d_models # diffevoが元のディレクトリとする
mkdir data
python diffusion.py
dataディレクトリを作成してからプログラムを実行しないとエラーが出ます．
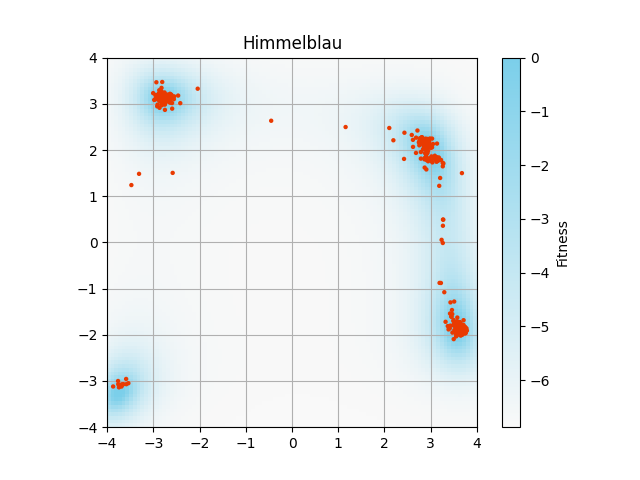
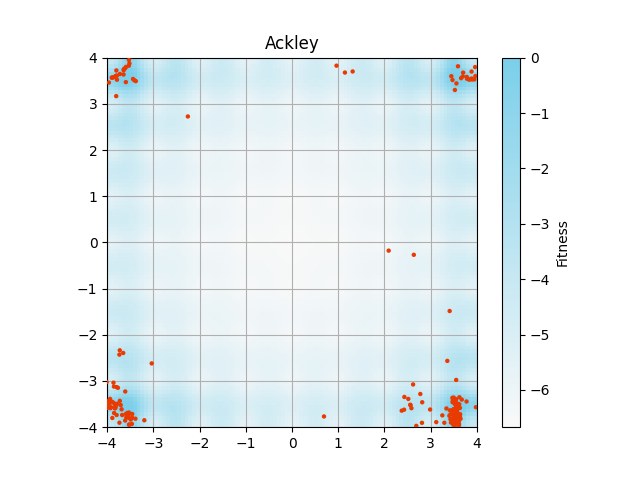
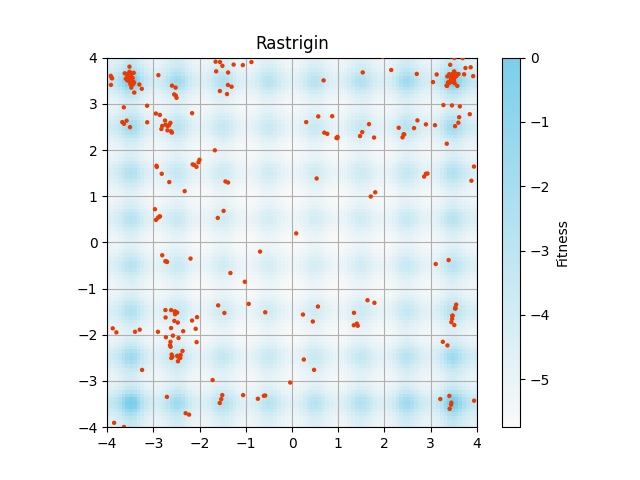
図3について
2024/10/20現在，hadesとfoobenchという謎の非公開パッケージがあるので，完全な再現は困難です．Issuesによると，その内パッケージがリリースされるそうです．
この記事では，CMAESとPEPGの処理が書かれているhadesは無視します．
拡散進化アルゴリズムのみ動かすことを目指します．
ベンチマーク関数
ベンチマーク関数が書かれているfoobenchパッケージは，以下のように再現します．
import torch
class Objective:
def __init__(self, foo, maximize, limit_val):
self.foo_name = foo
self.maximize = maximize
self.limit_val = limit_val
self._evaluate_func = {
"rosenbrock": self._rosenbrock,
"beale": self._beale,
"himmelblau": self._himmelblau,
"ackley": self._ackley,
"rastrigin": self._rastrigin,
}[foo]
def __call__(self, x: torch.Tensor) -> torch.Tensor:
x_clamped = torch.clamp(x, min=-4, max=4)
result = self._evaluate_func(x_clamped)
return -result if self.maximize else result
def _rosenbrock(self, X: torch.Tensor) -> torch.Tensor:
return torch.sum(
100.0 * (X[..., 1:] - X[..., :-1] ** 2) ** 2 + (X[..., :-1] - 1) ** 2,
dim=-1,
)
def _beale(self, X: torch.Tensor) -> torch.Tensor:
x, y = X[..., 0], X[..., 1]
return (
(1.5 - x + x * y) ** 2
+ (2.25 - x + x * y**2) ** 2
+ (2.625 - x + x * y**3) ** 2
)
def _himmelblau(self, X: torch.Tensor) -> torch.Tensor:
x, y = X[..., 0], X[..., 1]
return (x**2 + y - 11) ** 2 + (x + y**2 - 7) ** 2
def _ackley(self, X: torch.Tensor) -> torch.Tensor:
a, b, c = 20, 0.2, 2 * torch.pi
d = X.size(-1)
sum1 = torch.sum(X**2, dim=-1)
sum2 = torch.sum(torch.cos(c * X), dim=-1)
term1 = -a * torch.exp(-b * torch.sqrt(sum1 / d))
term2 = -torch.exp(sum2 / d)
return term1 + term2 + a + torch.exp(torch.tensor(1.0))
def _rastrigin(self, X: torch.Tensor) -> torch.Tensor:
A = 10
return A * X.size(-1) + torch.sum(
X**2 - A * torch.cos(2 * torch.pi * X), dim=-1
)
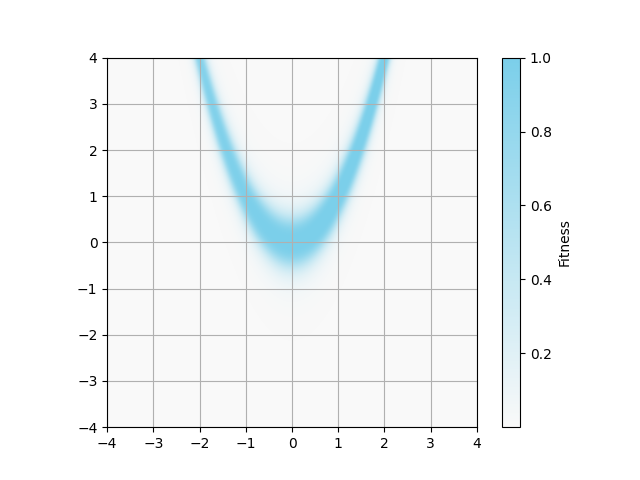
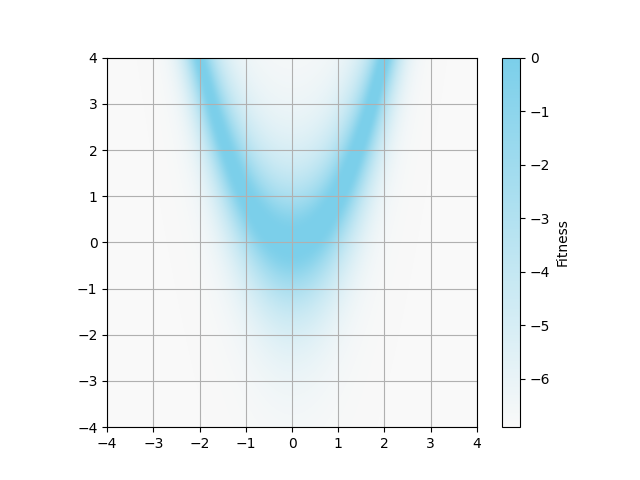
論文ではwe constrain the range of x and y to (−4, 4)と書かれていますが，
アルゴリズム側で変数範囲を制限する処理がありません．
そのため，解の評価時に範囲外の変数値を-4又は4に一時的に置き換えています．
（x_clamped = torch.clamp(x, min=-4, max=4)が該当）
また，foobench.pyの関数は，以下のようにラップされています．
def wrapped_obj(x):
d = abs(obj(x) - target) / scale
return eps / (d ** p + eps)
eps=0.001，p=2であり，targetとscaleは，問題毎に個別に設定されています．
つまり，この論文では特殊な加工をしたベンチマーク関数を取り扱っています．
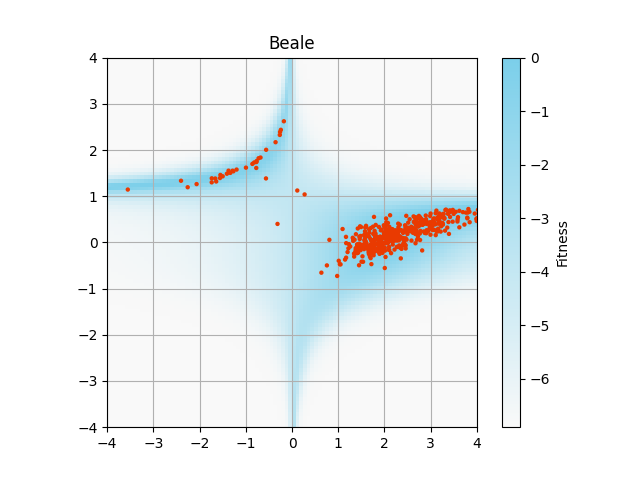
Rosenbrock関数とBeale関数は，大域的最適解(global optima)が1つの最適化問題です．
その他の関数は，大域的最適解が4箇所に分布する多峰性(multi-modal)最適化問題です．
メイン関数
plotbenchmark.pyを参考に，main.pyを作成します．
import matplotlib.pyplot as plt
from diff_evo import DiffEvo_benchmark
import torch
import numpy as np
import random
objs = ["rosenbrock", "beale", "himmelblau", "ackley", "rastrigin"]
if __name__ == '__main__':
# set random seed for reproducibility
seed = 10
torch.manual_seed(seed)
np.random.seed(seed)
random.seed(seed)
plt.figure(figsize=(12, 9))
DiffEvo_benchmark(objs, num_steps=25, plot=True, num_pop=512)
plt.tight_layout()
plt.savefig('benchmark.png')
plt.close()
乱数seedの記述は，不要かもしれません．
main.pyとfoobench.pyをdiffevo\experiments\benchmarksに置き，main.pyを実行すると図3と同様の画像が得られます．
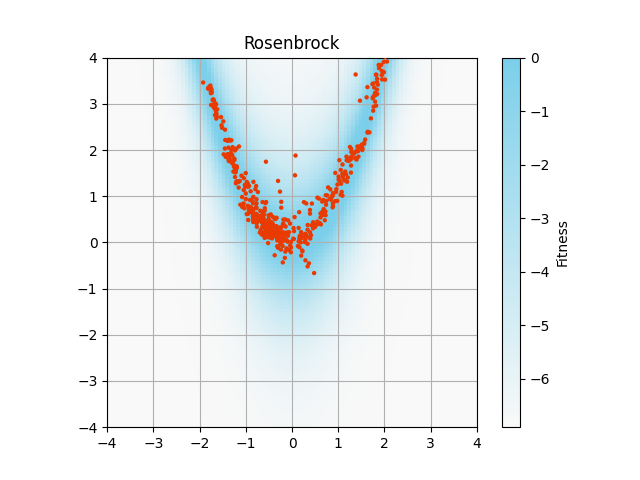
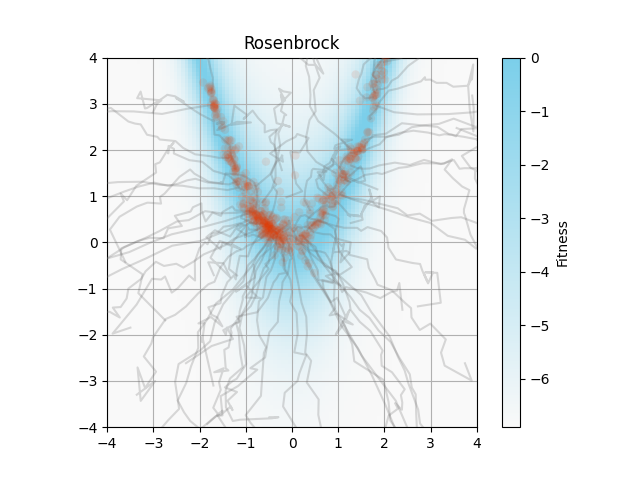
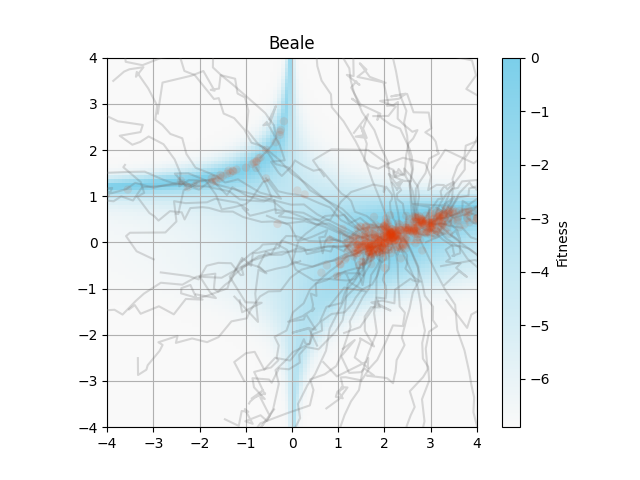
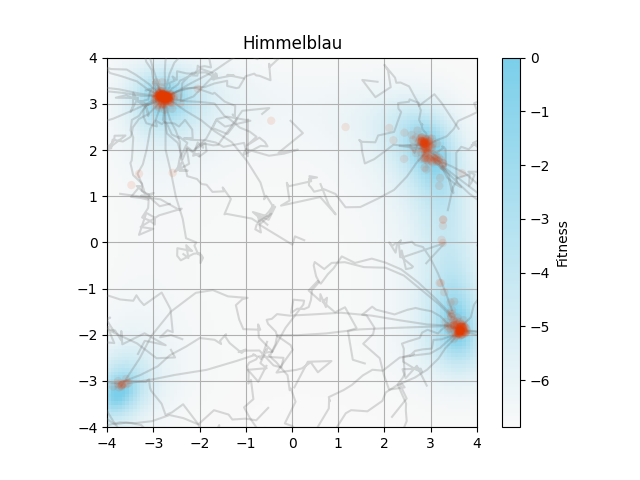
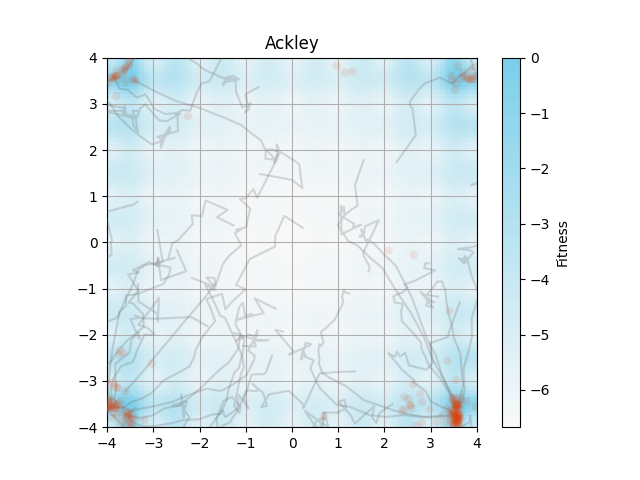
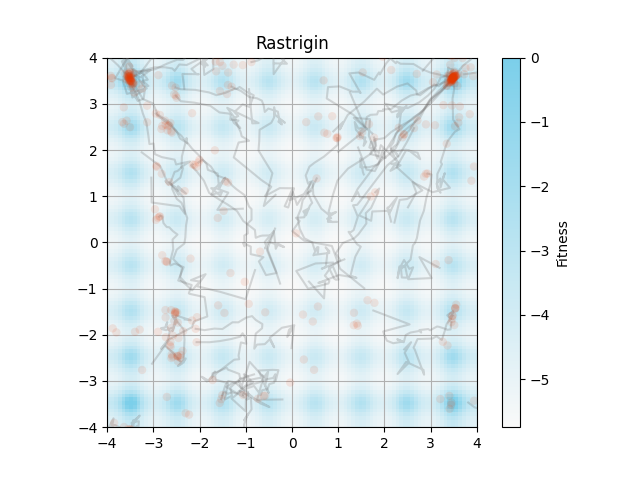
コードの一部を変更すると，以下の画像が得られました．
 |
 |
|---|---|
| 加工Rosenbrock関数の景観 | 論文画像で使われている景観 |
 |
 |
| 最終的に得られた512個の解集合 | 解集合＋64個体の軌跡 |
 |
 |
| 加工Beale関数の景観 | 論文画像で使われている景観 |
 |
 |
| 最終的に得られた512個の解集合 | 解集合＋64個体の軌跡 |
 |
 |
| 加工Himmelblau関数の景観 | 論文画像で使われている景観 |
 |
 |
| 最終的に得られた512個の解集合 | 解集合＋64個体の軌跡 |
 |
 |
| 加工Ackley関数の景観 | 論文画像で使われている景観 |
 |
 |
| 最終的に得られた512個の解集合 | 解集合＋64個体の軌跡 |
 |
 |
| 加工Rastrigin関数の景観 | 論文画像で使われている景観 |
 |
 |
| 最終的に得られた512個の解集合 | 解集合＋64個体の軌跡 |
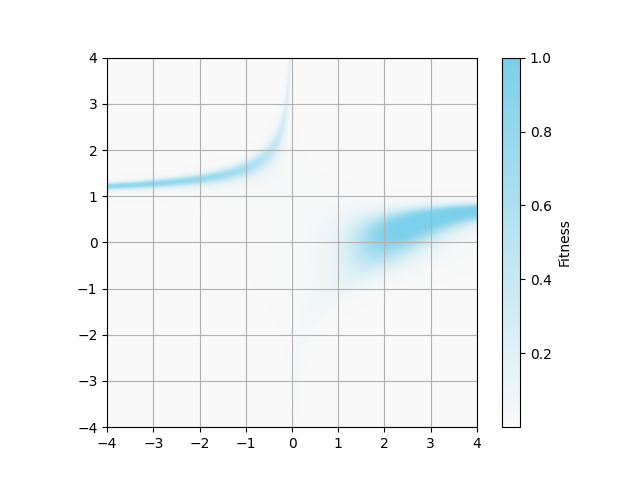
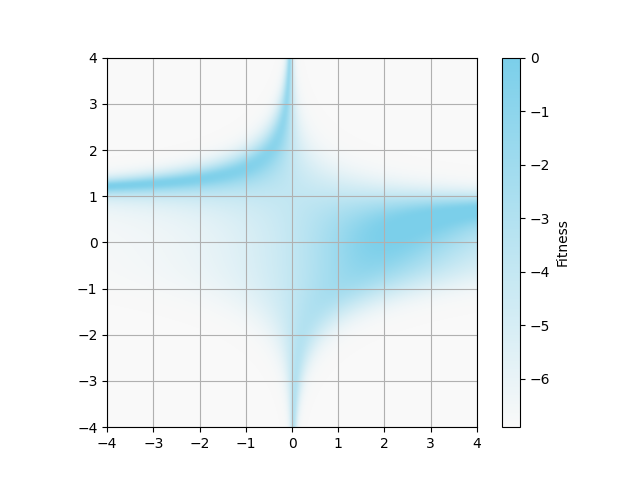
アルゴリズムでは区間$(0, 1]$のFitnessを使っていますが，論文の画像では$\log(~\text{Fitness}+10^{-3}~)$で背景描画をしています．
自分の再現では図の描画範囲外にも解が分布しています．
表1について
表1の再現実験をすると，以下の結果が得られました．
| Rosenbrock | Beale | Himmelblau | Ackley | Rastrigin |
|---|---|---|---|---|
| 4.89 (1.00) | 4.73 (1.00) | 3.05 (0.99) | 3.05 (0.99) | 4.37 (0.87) |
表は，拡散進化アルゴリズムが最終的に獲得した上位 64/512 個の解による結果です．
左がシャノン・エントロピーの値，右の括弧が64個体の平均fitnessです．
獲得した最上位解のfitness（100試行の平均）は，以下の通りでした．
| 元となる関数名 | fitness | 1-fitness（最適値1との差） |
|---|---|---|
| Rosenbrock | 0.9999985021352767 | 1.50e-6 |
| Beale | 0.9999956798553467 | 4.32e-6 |
| Himmelblau | 0.9999914211034775 | 8.58e-6 |
| Ackley | 0.9996752345561981 | 3.25e-4 |
| Rastrigin | 0.9469611895084381 | 5.30e-2 |
終わりに
一部で話題になっている？論文の再現を試みました．
不完全でも論文で利用したプログラムを公開している点を何よりも高く評価したいです．
図4の再現プログラムもありましたが，試す前に力尽きました．
査読前の論文なので当然ですが，これから議論や改善をしていくことが可能です．
論文を大幅に改稿・ブラッシュアップした上で，査読に出されると良いと思いました．