距離学習(MetricLearning)は画像認識に使われている学習の1つです。
次元空間において同じラベルのものを近く、違うラベルのものを遠く置くことができるモデルを作ることが目的で、
分類するクラスが決まっていない、人間の顔の認識や
2つ物体が同じかどうかを判断する同違判別などでよく使われます。
今回はその距離学習に使われる2つのLossを理解し、実装していきたいと思います。
初心者の理解、実装なので間違っている所があればご教授願います。
N-Pair Sampling
距離を学習する方針としては画像を何個か取り出し、特徴量を抽出し、その距離をLossとすることで学習していきます。
ここで画像を何枚使うかで様々なモデルがあります。
単純なものから、2枚で学習していくシャムネットワーク、3枚で学習していくトリプレットネットワークが開発され、現在も使われています。
しかしより多くの画像を使って相対的距離を測ろうとしたのがこのN-Pair-Samplingです。
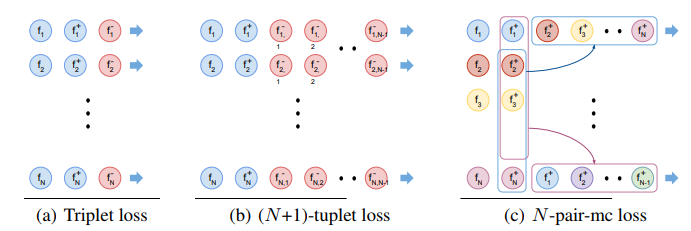
図引用[http://www.nec-labs.com/uploads/images/Department-Images/MediaAnalytics/papers/nips16_npairmetriclearning.pdf)
名前の通りをまず作るN個のクラスから2枚ずつ画像を取り出し、
そしてそれぞれの特徴量を計算してそこからN組のデータセットをつくります。
ここでその都度N+1個のベクトルを計算(図の(b))するのではなく、
N組を一度で計算してそこからデータセットを作っていく(図の(c))ので計算コストが少なくなります。
実装は2つのテキストファイルを作り出すようにしています。
1つはすべての画像のパス、もう1つがサンプリングされたインデックスです。
dataset側で1行ずつ読み込んでembeddingNetに入れるといいと思います。
自分が使ったデータのラベルが数字だったのでnp.whereを使いましたがもっといい方法があるかもしれません。
def n_pair_sampling(base_dir, path_text, n_pair_index_text, epoch_number, N):
labels = os.listdir(base_dir)
label_names = []
for label in tqdm(labels):
images = os.path.join(base_dir, label)
for im_name in os.listdir(images):
label_names.append(int(label))
path = os.path.join(label, im_name)
with open(path_text, mode='a') as f:
f.write("{}\n".format(path))
label_names = np.array(label_names)
for _ in tqdm(range(epoch_number)):
pair_samples = []
categories = [int(i) for i in os.listdir(base_dir)]
select_classes = np.random.choice(categories, N, replace=False)
for select_class in select_classes:
pair_sample = np.random.choice(np.where(label_names==select_class)[0], 2, replace=False)
#[x1, x2]
pair_samples.append(pair_sample)
pair_samples = np.array(pair_samples)
# print("pair", pair_samples)
anchors = pair_samples[:,0]
positives = pair_samples[:,1]
# print("anchors", anchors,"positives" , positives)
with open(n_pair_index_text, mode='a') as f:
for anchor_index in anchors:
f.write("{} ".format(anchor_index))
f.write(",")
for postive_index in positives:
f.write("{} ".format(postive_index))
f.write("\n")
N-Pair Loss
論文内ではN-Pair-mc lossと書かれています。
N組で学習するのでLossも変えなければなりません。しかしやっていることはTriplet lossと同じで、ベクトルの距離を使って同じクラスのものを近づけ違うクラスを遠ざけています。
L_{n-pair-mc}(\{(x_i,x_i^+)\}_{i=1}^N;f)=\frac{1}{N}\sum^N_{i=1}\log(1+\sum_{j\neq{i}}\exp(f^T_if^+_j-f^T_if^+_i))
実装
class n_pair_mc_loss():
def __init__(self):
super(n_pair_mc_loss, self).__init__()
def forward(self, f, f_p):
n_pairs = len(f)
term1 = torch.matmul(f, torch.transpose(f_p, 0, 1))
term2 = torch.sum(f * f_p, keepdim=True, dim=1)
f_apn = term1 - term2
mask = torch.ones_like(f_apn) - torch.eye(n_pairs).cuda()
f_apn = f_apn * mask
return torch.mean(torch.logsumexp(f_apn, dim=1))
Angular Loss
Angular Lossはangularつまり角度を使ったlossです。
いままではベクトル同士の距離を使って空間内で移動させてたものを角度を使うことでより正確に移動できるという考えです。
イメージとしては基準の角度を設定して、negativeがその閾値を超えた時矯正する感じです。
論文内ではα=45度もしくはα=36度のときに良い結果が出たようです。
角度を使うので一度に使うベクトルは3つ以上で、
3つのみで計算する、つまりTripletSamplingで使う通常版と、
それをN-Pair-Samplingで使えるように拡張した2つがあります。
通常版(triplet版)
l_{ang}(\Gamma)=[||x_a-x_p||^2-4\tan^2\alpha||x_n-x_c||^2]_{+}
通常版の実装
class AngularLoss(nn.Module):
def __init__(self, alpha=45, in_degree=True):
super(AngularLoss, self).__init__()
if in_degree:
alpha = np.deg2rad(alpha)
self.tan_alpha = np.tan(alpha) ** 2
def forward(self, a, p, n):
c = (a + p) / 2
sq_dist_ap = (a - p).pow(2).sum(1)
sq_dist_nc = (n - c).pow(2).sum(1)
loss = sq_dist_ap - 4*self.tan_alpha*sq_dist_nc
return F.relu(loss).mean()
n-pair版
l_{ang}(B)=\frac{1}{N}\sum_{x_a\in{B}}\{log[1+\sum_{\substack{x_n\in{B}\\y_n\neq{y_a,y_p}}}exp(f_{a,p,n})]\}
n-pair版の実装
class Angular_mc_loss(nn.Module):
def __init__(self, alpha=45, in_degree=True):
super(Angular_mc_loss, self).__init__()
if in_degree:
alpha = np.deg2rad(alpha)
self.sq_tan_alpha = np.tan(alpha) ** 2
def forward(self, f, f_p, with_npair=True, lamb=2):
n_pairs = len(f)
term1 = 4 * self.sq_tan_alpha * torch.matmul(f + f_p, torch.transpose(f_p, 0, 1))
term2 = 2 * (1 + self.sq_tan_alpha) * torch.sum(f * f_p, keepdim=True, dim=1)
f_apn = term1 - term2
mask = torch.ones_like(f_apn) - torch.eye(n_pairs).cuda()
f_apn = f_apn * mask
loss = torch.mean(torch.logsumexp(f_apn, dim=1))
if with_npair:
loss_npair = self.n_pair_mc_loss(f, f_p)
loss = loss_npair + lamb*loss
return loss
@staticmethod
def n_pair_mc_loss(f, f_p):
n_pairs = len(f)
term1 = torch.matmul(f, torch.transpose(f_p, 0, 1))
term2 = torch.sum(f * f_p, keepdim=True, dim=1)
f_apn = term1 - term2
mask = torch.ones_like(f_apn) - torch.eye(n_pairs).cuda()
f_apn = f_apn * mask
return torch.mean(torch.logsumexp(f_apn, dim=1))
lossの引数であるf,f_pを下図に示します。
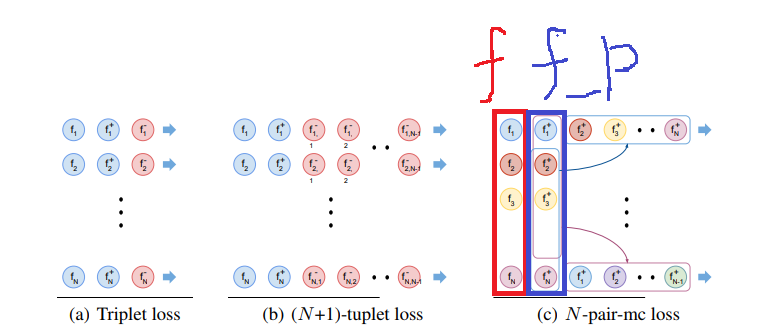
つまりN組作ったペアのうち、片方をf、もう片方をf_pとしてlossに入れます。
最後に
今回の2つのlossは埋め込みベクトルを直接計算しましたが、SphereFace, CosFace, ArcFaceのようなクロスエントロピー誤差を使えるようなモデルもあるみたいです。
距離学習は正解データが少ない場合などビジネスで活用される機会が多いと思うので、これからも発展していくと思います。
参考
https://github.com/ronekko/deep_metric_learning
https://alis.to/whey/articles/KOw49OXdyz5R
https://qiita.com/whey_yooguruto/items/34ee22d63bb6e260a6ba
n-pair samplingの論文
angular lossの論文