「パターン認識と機械学習 上」を読んで勉強しましたが、パラメータについての解釈がいまいちピンとこなかったので可視化できるツールを作ってみました。
目的
PRML上2章に出てくるいろんな分布の可視化。
パラメータを自由に変更して、それに伴う分布の変化を確認できるようにする。
使ったもの
PRML上
Python3.5
研究室の先生
ライブラリ
requirements.txt参照 ->https://github.com/tnyo43/PRMLstudy/blob/master/requirements.txt
実装には全てmatplotlibを使ってもよかったのですが、PyQtでUIを作ったのでグラフもPyQtで作りました。
コード
GitHubにあります
https://github.com/tnyo43/PRMLstudy
以下、実装したものを紹介していきます。分布についての説明も少しつけていますが、勉強中で、かつ今回は実装メインなので、概念に関する解釈は間違っているかもしれません。
ベータ分布
{\rm Beta}(\mu | a, b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1} \tag{2.13}
で定義される分布。0 $\le \mu \le $1の範囲内での$\mu$の確率密度を表し、
\int {\rm Beta}(\mu | a, b)d\mu = 1 \tag{2.14}\\
E[\mu] = \frac{a}{a+b} \tag{2.15}
{\rm var}[\mu] = \frac{ab}{(a+b)^2(a+b+1)} \tag{2.16}
の性質を持ちます。a、bはμの分布を決める超パラメータ。本書では二項分布の事前分布として紹介されています。
ツール
$python BetaFunction.py
を実行。ツールが起動します。
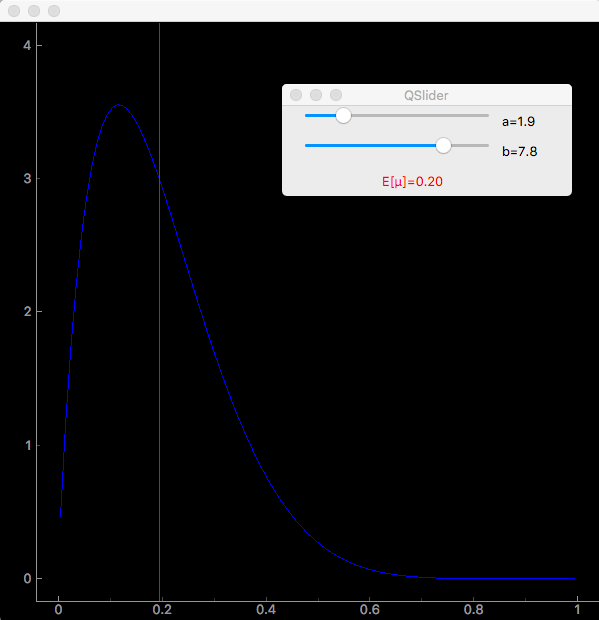
実行画面はこんな感じです。スライダーで超パラメータa、bの値を変化させると、青で表示された分布が変わっているのがわかります。赤い線はベータ分布の平均です。超パラメータを変更すると、
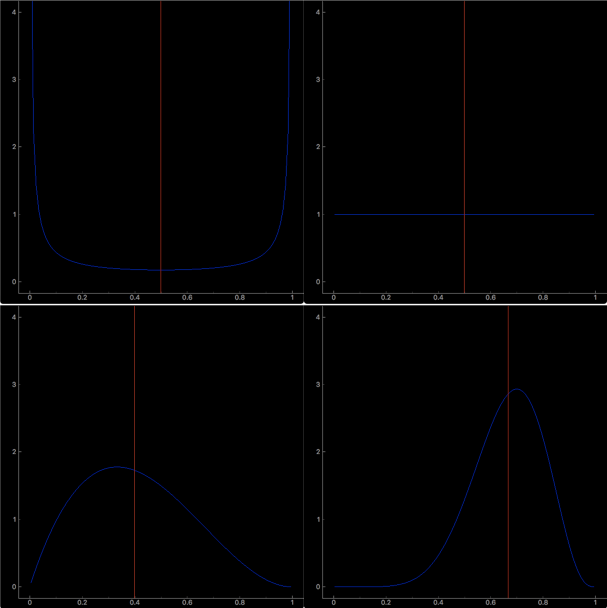
上のグラフの超パラメータはそれぞれ
(左上)$a=0.1, b=0.1$
(右上)$a=1, b=1$
(左下)$a=2, b=3$
(右下)$a=8, b=4$
超パラメータを変更すると分布が変化していることがわかります。逐次ベイズ推論では段階を踏むごとに超パラメータの値が更新されていくようです。
ディリクレ分布
{\rm Dir}(\boldsymbol{\mu} |\boldsymbol{\alpha}) =
\frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)}\prod^K_{k=1}\mu_k^{\alpha_k-1} \tag{2.38}
ただし
\alpha_0 = \sum^K_{k=1}\alpha_k \tag{2.39}\\
0 \le \mu_k \le 1\\
\sum^K_{k=1}\mu_k=1\\
多項分布のパラメータ${\mu_k}$に対する事前分布事前分布に利用されるらしいです。
ツール
ツールは3変数の多項分布の確率密度分布を表示しています。
$python DirichletDistribution.py
以下のようなツールが起動します。
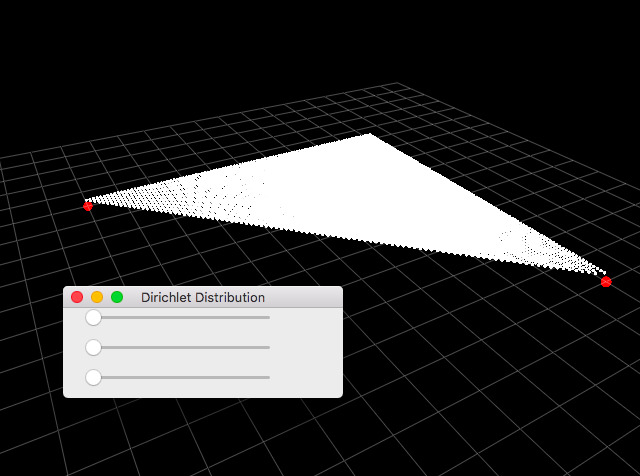
確率密度の大きさをそれぞれの点の高さで表現しています。以下、パラメータ$\boldsymbol{\alpha}$を変更した様子をいくつか貼りました。パラメータは画像内のUI画面から確認できます。
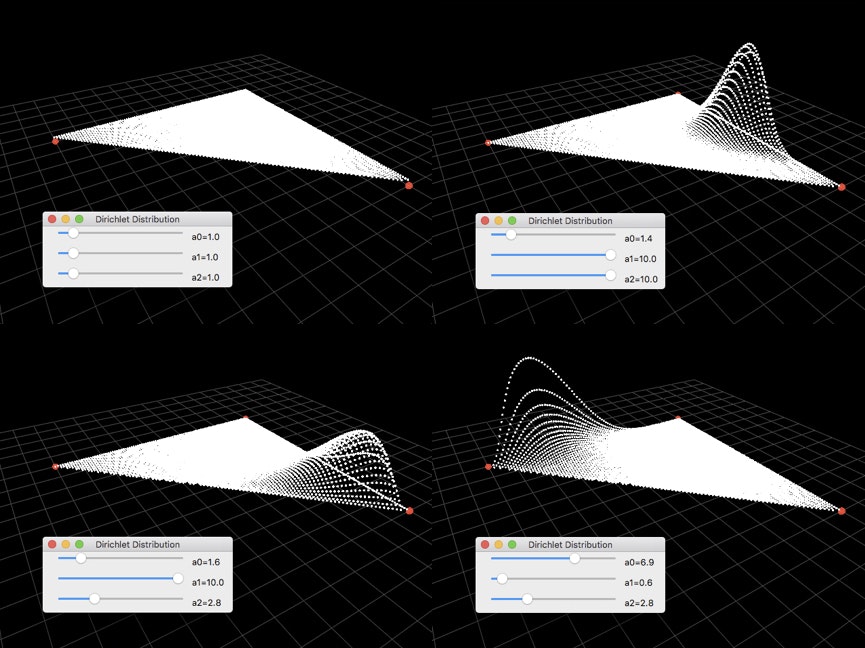
(2.38)から、$\alpha_k$は$\mu_k$の指数になっていることがわかります。大きい指数$\alpha_k$を持つ$\mu_k$が1に近いほど確率密度が大きくなっていますね。
ガウス分布に対するベイズ推定
分散$\sigma^2$が既知のガウス分布の平均$\mu$を、与えられたN個のデータ$\boldsymbol{X}= \left[x_1, ..., x_N\right]$から推定する問題。
$\mu$が与えられた時に観測データが生じる確率である尤度関数は、$\mu$の関数で、
p(\boldsymbol{x}|\mu) = \prod^N_{n=1}p(x_n|\mu) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}}\exp{\left\{ -\frac{1}{2\sigma^2}\sum^N_{n=1}(x_n - \mu)^2 \right\}} \tag{2.137}
この尤度関数に対して、事前分布$p(\mu)$をガウス分布とすると、共役事前分布となります。つまり、事前分布$p(\mu)$を
p(\mu) = \mathcal{N}(\mu | \mu_0, \sigma_0^2) \tag{2.138}
とすると、と事後分布$p(\mu|\boldsymbol{x})$は、
p(\mu|\boldsymbol{x}) \varpropto p(\boldsymbol{x}|\mu)p(\mu) \tag{2.139}
となます。これを計算すると、
p(\mu|\boldsymbol{x}) = \mathcal{N}(\mu | \mu_N, \sigma_N^2) \tag{2.140}
ただし
\mu_N = \frac{\sigma^2}{N\sigma_0^2 + \sigma^2}\mu_0 + \frac{N\sigma_0^2}{N\sigma_0^2+\sigma^2}\mu_{ML}\tag{2.141}\\
\frac{1}{\sigma_N^2} =\frac{1}{\sigma_0^2}+\frac{N}{\sigma^2} \tag{2.142}
\mu_ML = \frac{1}{N}\sum^N_{n=1}x_n \tag{2.143}
(2.142)より、データ数Nが増えるにつれて$\mu$の推定の分散が小さくなっていくことがわかります。
また、(2.141)の第一項はNの増加と共に小さくなり、第二項は(2.143)で定義される$\mu$の最尤推定解$\mu_{ML}$に近づくことがわかります。
逆にデータ数が少ない時、初期値として設定した事前分布の平均$\mu_0$と分散$\sigma_0^2$に大きく影響されるので、初期値の設定の仕方は大切そうです。
ツール
$python GaussianDistribution.py
を実行。3つのグラフとスライダなどが入ったUIが表示されます。
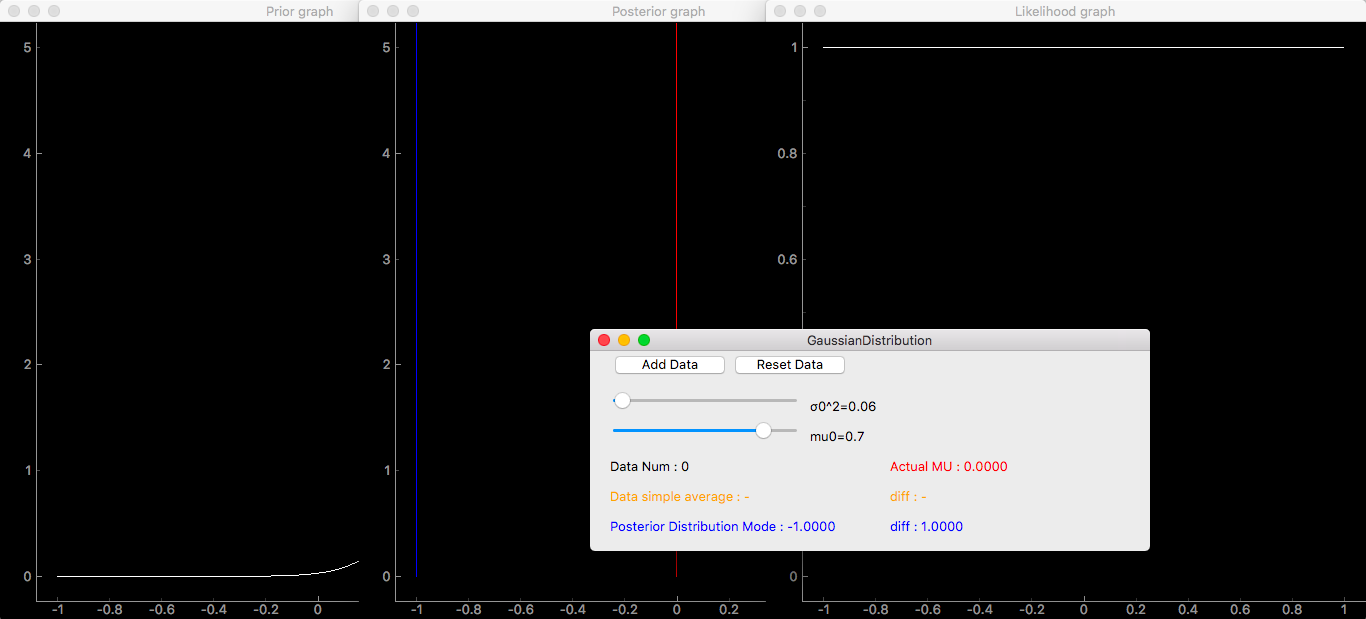
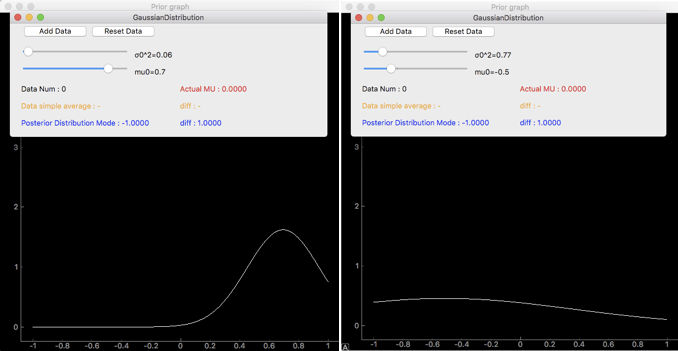
一つ目のグラフが事前分布で、スライダの$\sigma_0$、$\mu_0$にのみ依存します。例えば$\mu_0$=0.7、$\sigma_0^2$=0.06のときと、$\mu_0$=-0.5、$\sigma_0^2$=0.77のときはこんな感じです。
二つ目のグラフは尤度関数。これは観測データのみによって決まります。今回観測するデータは、分散$\sigma_0^2$=4、平均$\mu_0$=0のガウス分布に従います。(分散がかなり大きいですが、これくらいがちょうど違いがわかりやすかったのでこれにしました。)
横軸が平均$\mu$で、縦軸は観測データに対して$\mu$が平均としてどれほど尤もらしいかを表しています。大きさは($0 \le \mu \le 1$)のなかでの最大値を1に正規化しているので、数値自体に意味はないです。
観測データが0、1、2、5、10、30個の時の尤度関数のグラフは以下のようになりました。
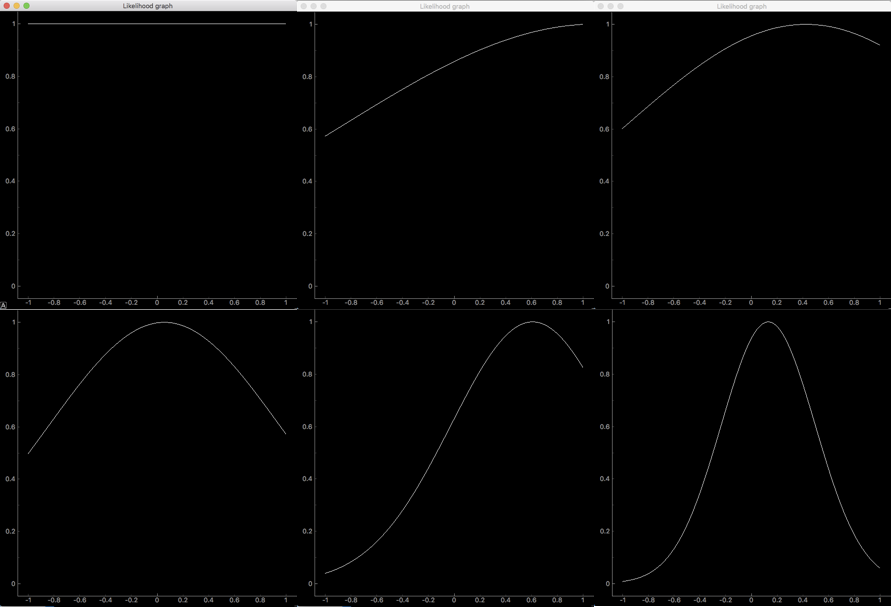
観測データが0個の時、もちろんどこに平均があるかがわからないので、尤度関数は一様になります。データが1つの時、観測した値を平均とするため、そこを最大とした曲線になります。データが増えていくごとに曲線の山が小さくなっているのは、もっとも平均としてふさわしい$\mu$の位置がはっきりとわかってくるからです。尤度関数の最大値を最尤推定解$\mu_{ML}$といいます。MLはおそらくMost Likelihoodの頭文字でしょう。
三つ目のグラフは事後分布です。事前分布のパラメータと観測データによって決まります。
実験
初期のパラメータを変化させながら事後分布の変化を見てみます。
7枚の画像のうち、左上が事前分布、そこから順に観測データが1、2、5個、下の段は左から順に観測データが10、20、30個の時の分布です。 赤い縦線はデータの真の平均値$\mu=0$、青い線は事後分布の最大となる$\mu_N$(2.141)、黄色い線は$\mu$の最尤推定解です(2.143)。
まずは$\sigma_0=0.51$、$\mu_0=0.0$のとき
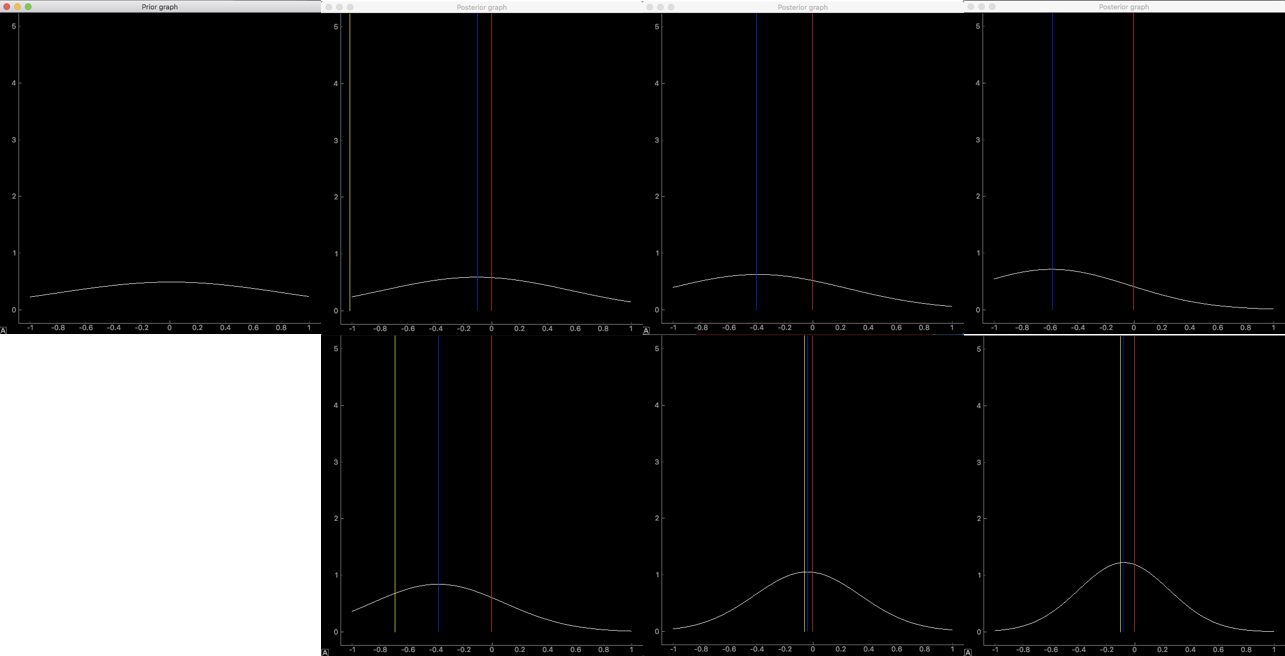
一つ目の観測データが右に大きくずれていますが、事前分布の平均が解と一致していて分散も小さいのであまり変化がなく、青の線で示した事後分布の最大値が赤の真の平均値に近いことがわかります。データが増えるごとにその距離も小さくなっています。曲線の山型が急になっているのは$\mu$の値が推定できてきたからです。
次に$\sigma_0=0.51$、$\mu_0=0.8$のとき
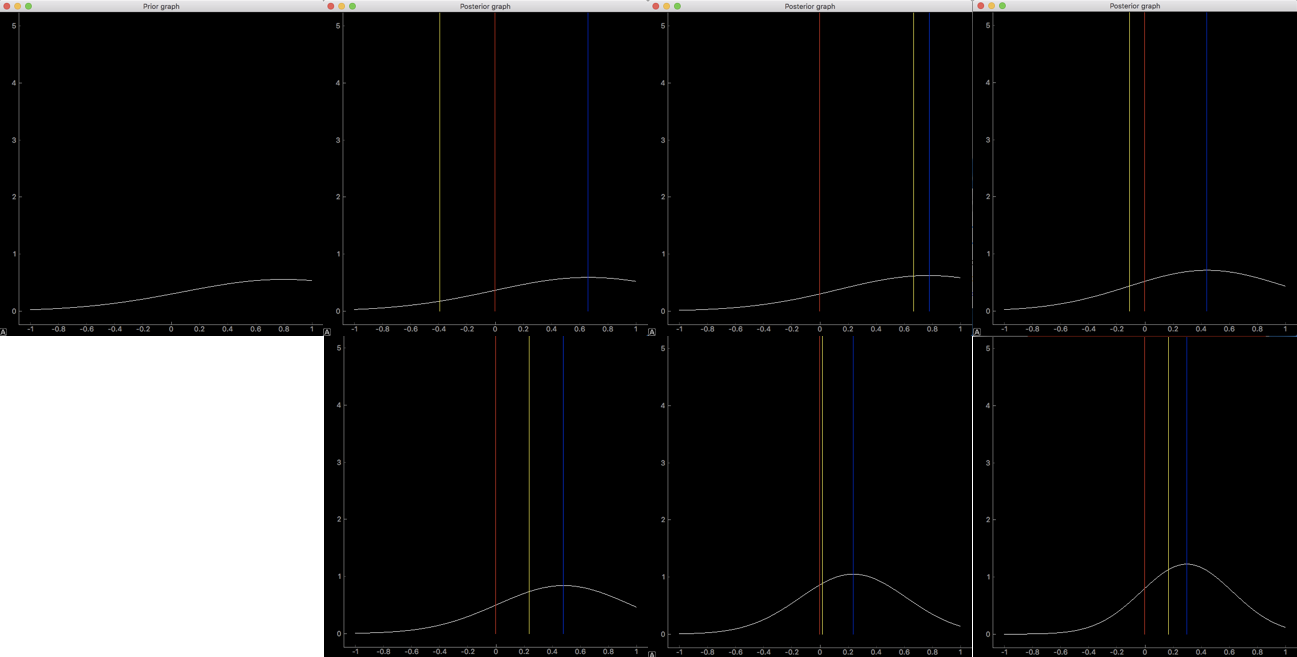
観測データが少ない時は事前分布と同じような形をとってうまく推定できていません。データが増えると真の平均値に近づきますが、それでも真の答えに近づくにはたくさんのデータが必要そうです。
次は$\sigma_0=2.23$、$\mu_0=0.0$のとき、
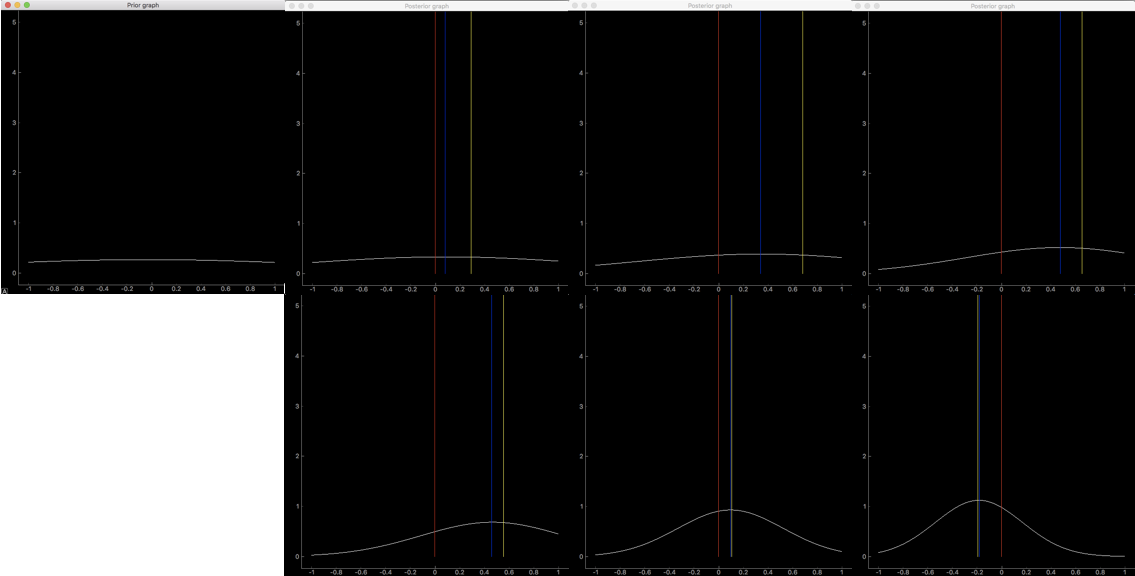
事前分布をみると平べったく広い範囲に分布していることがわかります。
$\sigma_0=0.51$、$\mu_0=0.0$のときに比べて、観測データが10個くらいまでは明らかに分布の山が小さいです。これは$\mu$の値を推定できていないということを意味します。分散が大きいとデータが少なすぎるときはほとんど推定として機能しないようです。さらに、ノイズに弱く、平均から大きく外れたデータが観測されると分布も大きく変化しました。
次は$\sigma_0=0.01$、$\mu_0=0.8$のとき、
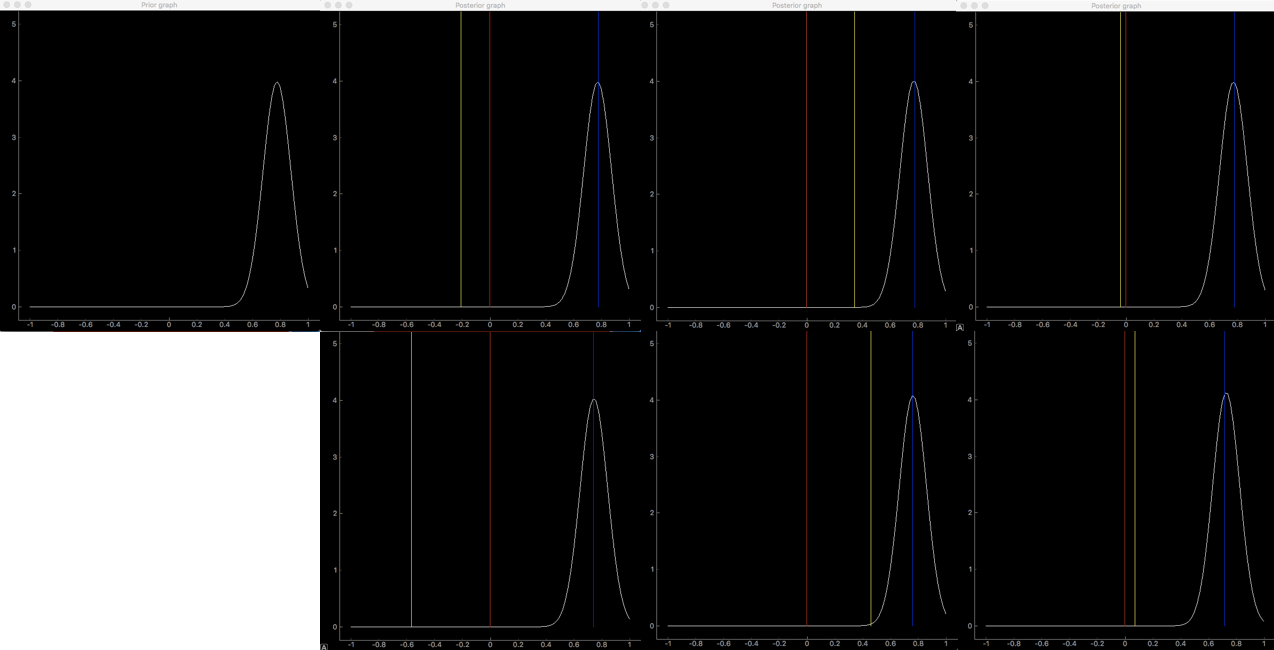
事前分布の分散が小さいと、入力データの影響を受けなくなります。30個の入力に対して分布がほとんど変化していません。ノイズには強くなりますが、観測データの情報を分布にうまく反映できていないと言えるでしょう。
考察
事前分布のパラメータ、特に分散、は観測データを分布に反映させる上で、ノイズの大きさと観測できるデータ数を考慮した上で適切に決定しなければならないようだ。
まとめ
今回はベータ分布、ディリクレ分布、ガウス分布に対するベイズ推定、それぞれのグラフを表示するツールを作成しました。実際に作ってみると解説の意味がよくわかるし、可視化できると理解が進みます。
読み進めて行きながら実装できそうなところはしてみようと思います。2章に出てくる他の確率分布は実装済みなので、近々アップしようと思います。