はじめに
はじめまして!
昨年の5月からプログラミングを始めたど素人ですが,今日からふと思ったこと,気になることをどんどん投稿していきたいと思います.
余談なんですが,研究自体はロボット×機械学習をテーマに様々な分野に展開しています.
ちなみに,写真は最近作った人工知能を搭載したエアーホッケーロボットで,小さな子供よりは強くなりました!
興味がある方はこちら

本日のテーマ
このページを見てくれたほとんどの人は,最小二乗法がどういうものかをご存知だと思います.
ただ,ウェブ上で二次元空間での最小二乗法を使った例はたくさん見てきたのですが,
三次元空間で使ったものがなかなかありませんでした...
なので,今回は,このよく使う最小二乗法を三次元空間でどのように使えばよいのかを簡単に紹介します.
環境
Python 3.6.5
ProductName:Mac OS X
ProductVersion:10.14
最小二乗法とは
みなさん!!最小二乗法とはそもそも何をするために使うのか知ってますか?
詳細は割愛しますが,簡単に説明すると
最小二乗法(least squares method)
測定で得られた数値を使って,適当なモデルから想定される1次関数,対数曲線など特定の関数を用いて近似するときに使うもの.
この近似を行う際に、残差の二乗和を最小とするような係数を決定すること.
数式や説明の詳細はこちら
二次元での最小二乗法
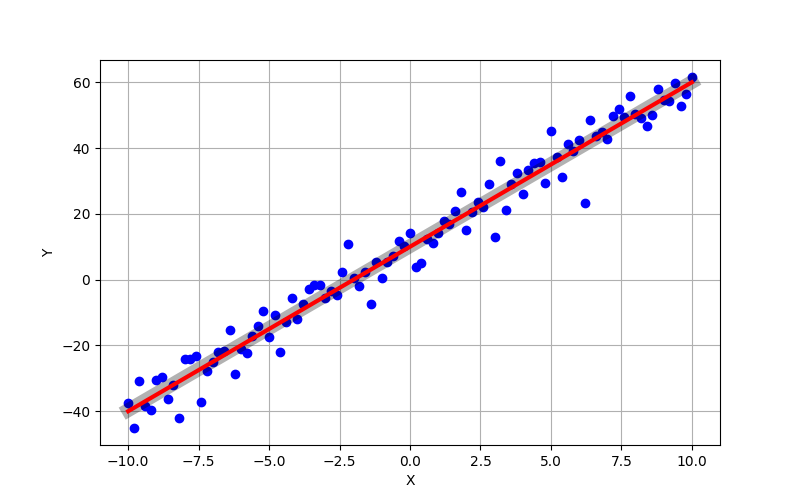
みなさん,二次元の最小二乗法を一度は経験したことがあると思うので,簡単な説明と図だけ.
図のようにあるサンプル点から,簡単に近似曲線を求めることができます.(図は線形近似)
二次元で最小二乗法を実装したい人はこちら
三次元での最小二乗法
それでは本日のテーマ**「三次元での最小二乗法」**に入っていきたいと思います.
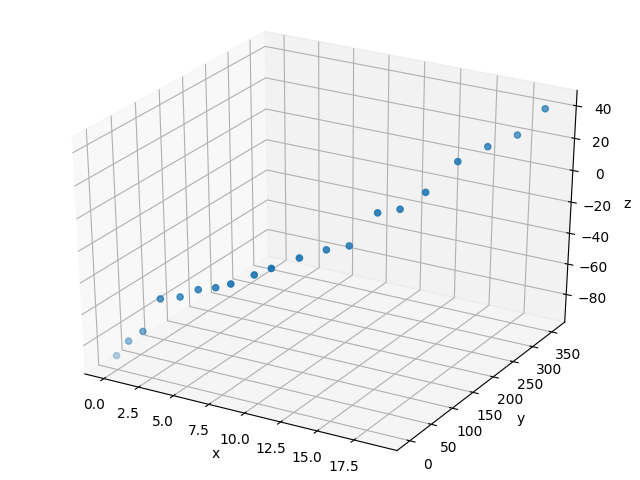
今回は,下の図のような点を用いて,三次元空間内で近似曲線を求めたいと思います.
(これは僕が適当に作った点であるので例として相応しいとはいえないかも...すいません)
僕が今回したフィッテングに用いた関数は,次のような多項式です.
f(x)=ax^2 + by^2 + cx + d y + e
このハイパーパラメータ(人が調整するべきパラメータ)
a,b,c,d,e
を最小二乗法を用いて最適化します.
コードは以下です.
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
from scipy import optimize
from mpl_toolkits.mplot3d import Axes3D
# サンプル点を作成
x = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19])
y = np.array([-1,-3,-1,9,21,30,37,39,59,65,95,123,142,173,191,216,256,292,328,358])
z = np.array([-89,-77,-69,-48,-47,-42,-40,-36,-32,-27,-24,-22,-21,-4,-3,5,19,24,27,40])
# フィッティングする関数を作成
def fiting_func(param,x,y,z):
residual = z - (param[0]*x**2 + param[1]*y**2 + param[2]*x + param[3]*y + param[4])
return residual
# ハイパーパラメータを初期化
param = [0, 0, 0, 0, 0]
# 最小二乗法を実装
optimised_param = optimize.leastsq(fiting_func, param, args=(x, y, z))
print(optimised_param)
# フィッティングする関数を求める
a = optimised_param[0][0]
b = optimised_param[0][1]
c = optimised_param[0][2]
d = optimised_param[0][3]
e = optimised_param[0][4]
print("a:",optimised_param[0][0])
print("b:",optimised_param[0][1])
print("c:",optimised_param[0][2])
print("d:",optimised_param[0][3])
print("e:",optimised_param[0][4])
f = a*x**2 + b*y**2 + c*x + d*y + e
# 3Dでプロット
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, y, z)
ax.plot(x, y, f)
# 軸ラベル
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
# 保存
plt.savefig('figure_3d.png')
# 表示
plt.show()
ハイパーパラメータを見てみると
a: -0.5551880910904999
b: 0.0007371156506096842
c: 10.113522462277956
d: 0.10962459408256231
e: -84.61701880472386
割と上手く近似できたのではないかと思います.
まとめ
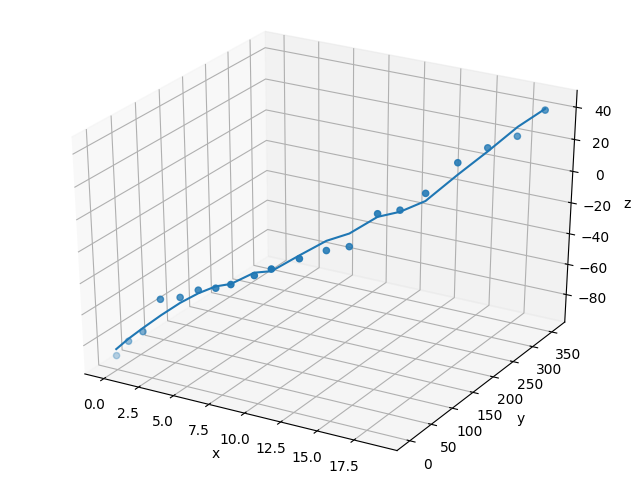
今回は三次元空間で最小二乗法を実装し,近似曲線を求めました.
少し,なめらかではないですが,上手くできたのではないかと思います.
もっといい方法などあると思うんで,是非コメントください!!!
最後まで読んでいただきありがとうございます ^_^