多項ロジスティック回帰分析とは？

多項ロジスティック回帰

• 多クラス分類を可能にしたロジスティック回帰

• 値域が[0,1],総和が1になるように線形予測子を変形しようとするモデル。

• 大きく「名義ロジスティック回帰」と「順序ロジスティック回帰」に分かれる

①名義ロジスティック…クラス間に特別な順序がない場合の多クラス分類
ex)男子=0,女子=1

②順序ロジスティック…クラス間に特別な順序がある場合の多クラス分類。
ex)好き=0,それほど好きではない=1,嫌い=2

多クラス分類の場合は

p1=〇の形にすると？

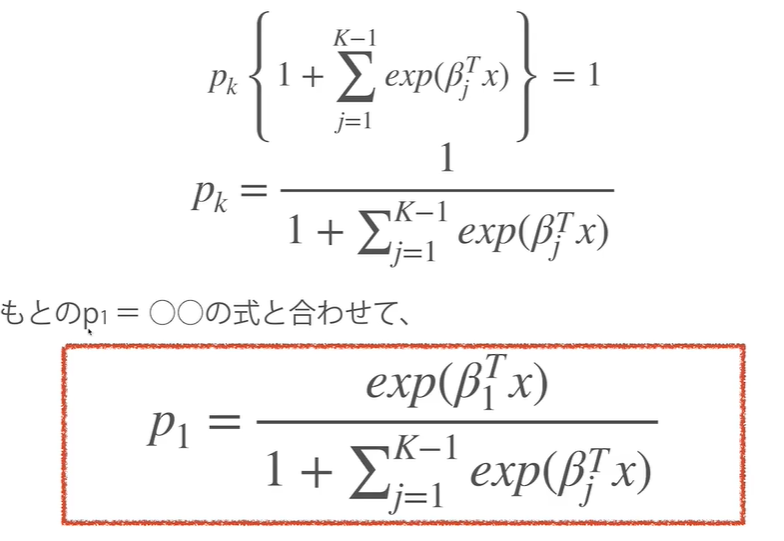
最適化方法とは？

実験

今回はsklearnライブラリのデータセットを使って分析をしてみたいと思います。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

digits = load_digits()
X=digits.data
y=digits.target

images_with_labels = list(zip(digits.images,digits.target))

plt.figure(figsize=(15,6))

for idx,(image,label) in enumerate(images_with_labels[:10]):
    plt.subplot(2,5,idx+1)
    plt.imshow(image,cmap=plt.cm.gray_r,interpolation="nearest")
    plt.title("{}".format(label),fontsize=25)
plt.show()

from sklearn.metrics import confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

scaler=StandardScaler()
X_scaled=scaler.fit_transform(X)

X_train,X_test,y_train,y_test=train_test_split(X_scaled,y,random_state=0)

print(log_reg.score(X_train,y_train))
print(log_reg.score(X_test,y_test))

prediction=log_reg.predict(X_test)
confusion = confusion_matrix(prediction,y_test) #混合行列生成
print(confusinon)