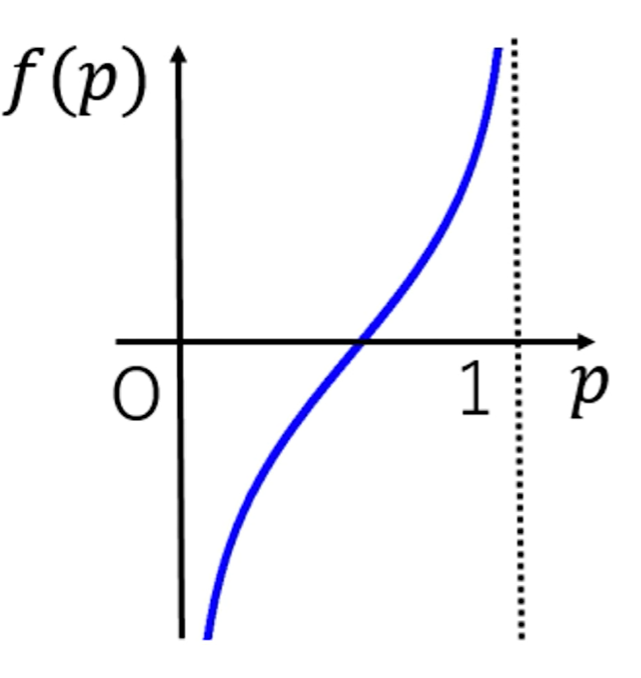
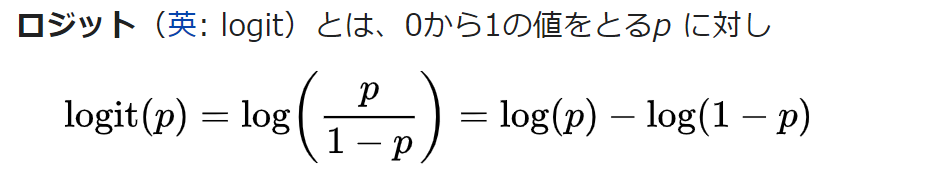ロジスティック回帰分析とは？

• いくつかの説明変数から確率を計算して、予測を行うモデル。

• 一般化線形モデルの一種。

• 「回帰」という名前が付いているが、「分類」のために使われることが多い。

一般化線形モデルとは？

• 応答変数が、正規分布以外の確率分布に従う場合にも使えるようにした線形モデル。

例えば、
〇　体重 = β0 + β1 × 身長
(体重は正規分布に従う変数)

✖　服のサイズ = β + β1 × 身長
(服のサイズは明らかに正規分布に従う変数ではない)

応答変数と線形予測子を対応させなければならない

応答変数がアイスの販売個数の場合は？

アイスの販売個数 = β0 + β1 × 気温
　(応答変数)　　　　　(線形予測子)

「アイスの販売個数」は正の数しか取りえないが、右辺は気温次第でマイナスになる可能性がある。

そこで！！
救世主となるリンク関数(log関数)を導入する。

log(アイスの販売個数) = β0 + β1 × 気温

応答変数が確率(合格率)の場合は？

✖ テストの合否(1,0) = β0 + β1 × 勉強時間
右辺は明らかに1又は0のみの値を取る式ではない。

✖ テストの合格率 = β0 + β1 × 勉強時間
しかし、これでもまだ不十分。合格率は0から1の範囲を取るはずだが、右辺はそうではない。

そこで!!
救世主となるリンク関数(logit関数)を導入する。

log(p/1-p) = β0 + β1 × 勉強時間
これをp=〇の形にすると、

p=1/{1+exp(-(β0 + β1 × 勉強時間))}
この式にすることで、右辺が0から1の範囲を取るようになる。

この式のパラメータβ0,β1を最適化することが目標。

「最適」をどう定義するのか？

尤度関数を考える。
n番目の人の予測値は

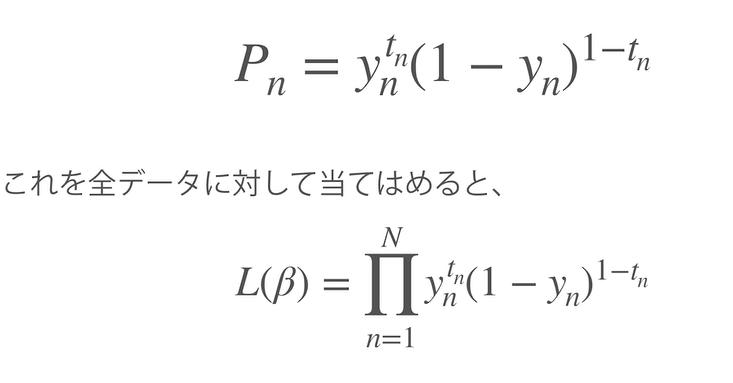
※tn…正解ラベル(0or1)
※yn…p=1/{1+exp(β0 + β1 × 勉強時間)}のn番目の人の出力値
目的は、この式の最大化。
しかし、掛け算は計算が複雑なうえに、確率の相乗を計算しようとすると、値が限りなく0に近づいてしまう。(アンダーフロー)。

【解決案】
①対数をとることで掛け算を解消。(足し算にできる)
②マイナスをつけることで、勾配降下法を実行できる。(勾配降下法は最小値を求めるのに適しているから)

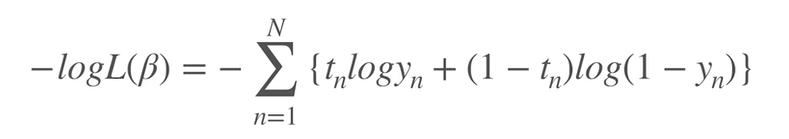
上記の式を交差エントロピー誤差関数と呼ぶ。

この関数を勾配降下法を用いてβ0,β1をそれぞれ微分することでパラメータの最適値を求める！

実験

今回はsklearnライブラリのデータセットを使って分析をしてみたいと思います。

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris

iris=load_iris()
df=pd.DataFrame(iris.data,columns=iris.feature_names)
df["target"]=iris.target

X=iris.data[50:,2].reshape(-1,1) #targetの0~2の中で1,2のみを取得する。
y=iris.target[50:]

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split


scaler=StandardScaler()#標準化
X_scaled=scaler.fit_transform(X)

X_train,X_test,y_train,y_test=train_test_split(X_scaled,y,random_state=0)

log_reg=LogisticRegression().fit(X_train,y_train)

print(model.coef_) #回帰変数の表示
print(model.intercept_) #回帰直線の切片

print(log_reg.score(X_train,y_train)) #決定係数を出力。
print(log_reg.score(X_test,y_test)) #決定係数を出力。