L1正則化に基づくロジスティック回帰モデル

はじめに

L1罰則つきロジスティック回帰モデル　(L1-penalized logistic regression model)は、機械学習において広く用いられる手法の一つです。通常のロジスティック回帰モデルにL1罰則を導入することで、スパース性を持たせ、特徴選択を行うことが可能になります。特に因果推論系のmoduleであるEconMLなどでは、傾向スコアの推定のデフォルトによく用いられている印象があります。書いておくと誰かの目には止まるかもしれないと思ったので、動かすためのコードも一緒に書いてあるので、参考になれば嬉しい限り。

L1-罰則つきロジスティック回帰モデル

このモデルは、ベルヌーイ分布の対数尤度最大化問題（以下では符号を変えることで最大化問題としています）を、L1罰則下で解くことで、回帰係数のスパース化を行います。この最小化問題は以下のように書くことができます。

$$ \min_{\beta} \left( - \sum_{i=1}^{N} \left[ y_i \log(P(y_i=1|X_i)) + (1 - y_i) \log(1 - P(y_i=1|X_i)) \right] + \lambda \sum_{j=1}^{p} |\beta_j| \right) $$

あとはこれを解くだけですが、L1罰則つきの最小化問題は回帰係数 $\beta$ での微分ができないので、最適化アルゴリズムを選択する必要がありますが、この辺りはたくさん記事が用意されているので省略。以下を参照してください。

実装

擬似データを生成して、モデルの当てはめを行います。Solverは、liblinearかsagaのいずれかを選択してください（と公式に書いてあります。少ないサンプルならliblinearが高速で、大規模なデータならsagaを選択しようとのこと）。

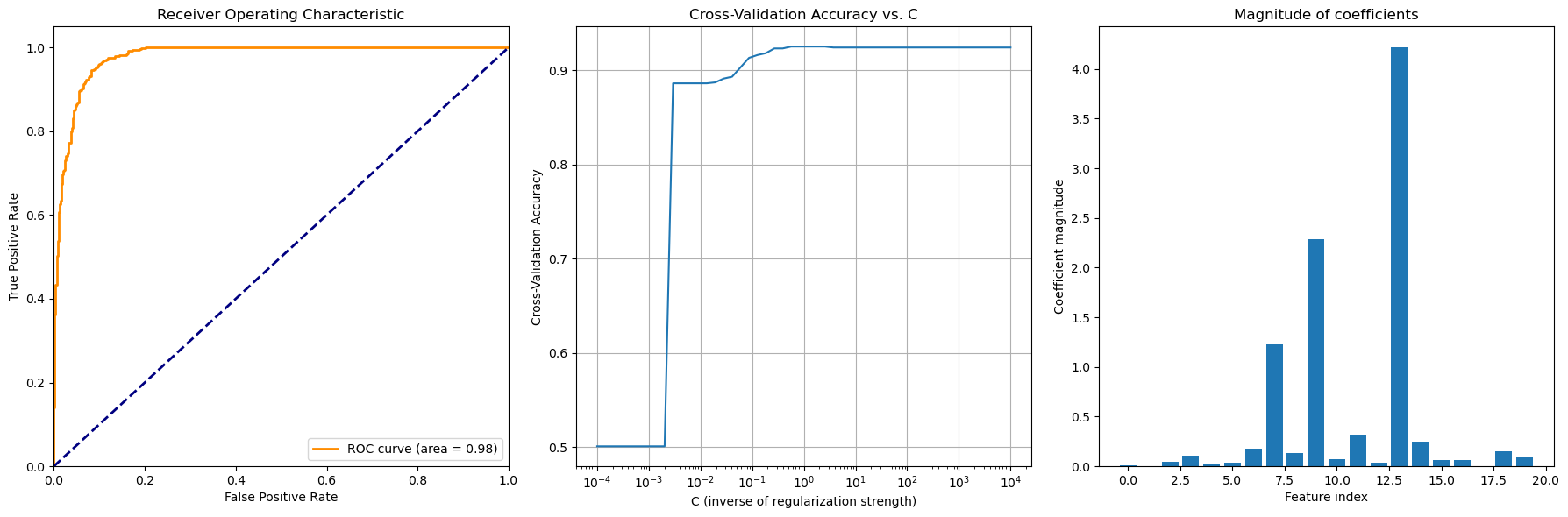
• 最終的に選択された$\lambda$の元での、モデルの推定精度を計算（ROC)
• ハイパーパラメータ $\lambda$ の選択に対するCross-validation accuracy
• 最終的に選択された$\lambda$ の元での回帰係数
  の3つを表示するコードが以下になります。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_curve, auc

# データ生成
X, y = make_classification(n_samples=1000, n_features=20, n_informative=3, n_redundant=0, n_clusters_per_class=1, random_state=42)

# L1-penalized Logistic Regression
logistic = LogisticRegression(penalty='l1', solver="saga", max_iter=10000)

# グリッドサーチによる最適な罰則ペナルティーの選択
param_grid = {'C': np.logspace(-4, 4, 50)}
grid_search = GridSearchCV(logistic, param_grid, cv=5, scoring='accuracy')
grid_search.fit(X, y)

# 最適なモデルの取得
best_model = grid_search.best_estimator_
best_model.get_params()

# 予測とROC曲線のプロット
y_score = best_model.decision_function(X)
fpr, tpr, _ = roc_curve(y, y_score)
roc_auc = auc(fpr, tpr)

# プロットの作成
plt.figure(figsize=(18, 6))

# ROC曲線のプロット
plt.subplot(1, 3, 1)
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")

# 正則化パラメータに対するスコアのプロット
plt.subplot(1, 3, 2)
plt.semilogx(param_grid['C'], grid_search.cv_results_['mean_test_score'])
plt.xlabel('C (inverse of regularization strength)')
plt.ylabel('Cross-Validation Accuracy')
plt.title('Cross-Validation Accuracy vs. C')
plt.grid(True)

# 係数の絶対値のプロット
plt.subplot(1, 3, 3)
coefficients = np.abs(best_model.coef_[0])
plt.bar(range(len(coefficients)), coefficients)
plt.xlabel('Feature index')
plt.ylabel('Coefficient magnitude')
plt.title('Magnitude of coefficients')

plt.tight_layout()
plt.show()

# 最適な罰則ペナルティー
print(f'Optimal penalty (C): {grid_search.best_params_["C"]}')
print(f'Best cross-validation accuracy: {grid_search.best_score_:.4f}')

罰則ペナルティーの変化に対する係数の変化

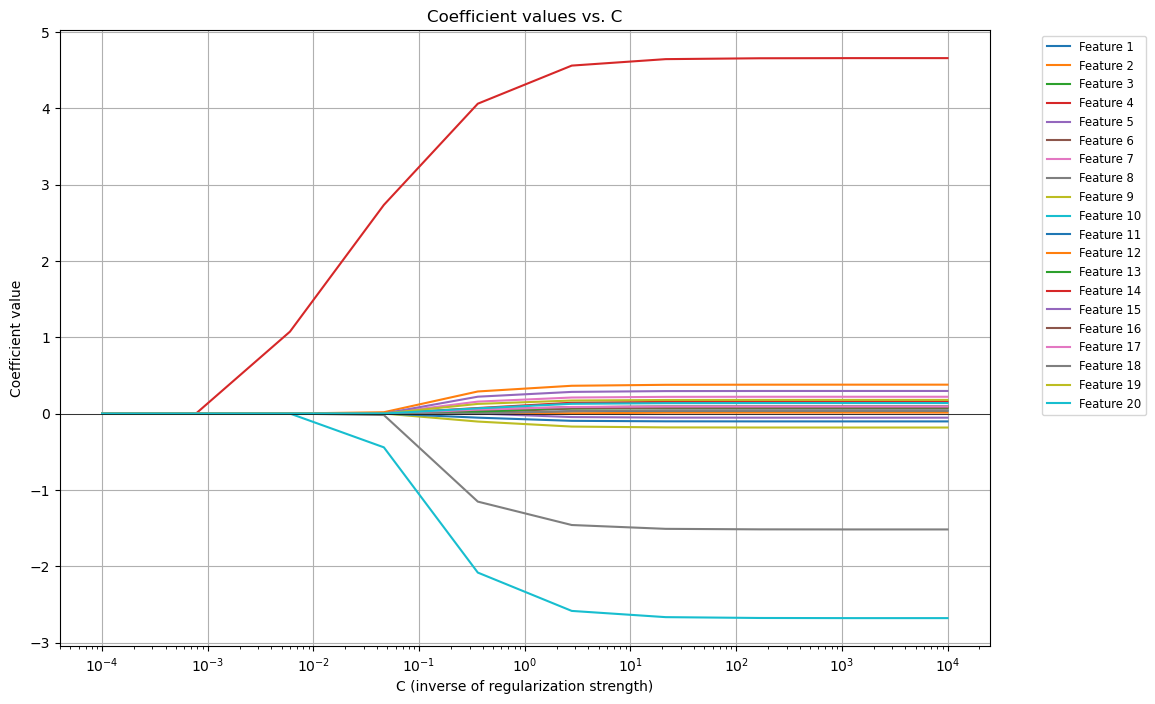
罰則パラメータが変化すると精度が変化する理由をもう少し深掘りするために、罰則パラメータ $\lambda$ が変化すると、回帰係数がどのように変化するかをプロットします。先ほどの真ん中の図で、$\lambda = 10^{-3}$から、$\lambda = 10^{-2}$になるところで精度が大きく改善しています。この辺りで、何が起こっているのかを確認すると、挙動理解に役立ちそうです。以下のコードで、$\lambda$　を変化した際の回帰係数の変化を確認します。

# 罰則ペナルティの異なる値
C_values = np.logspace(-4, 4, 10)

# 各C値に対する係数を格納するリスト
coefficients = []

for C in C_values:
    logistic = LogisticRegression(penalty='l1', C=C, solver='saga', max_iter=10000)
    logistic.fit(X, y)
    coefficients.append(logistic.coef_[0])

coefficients = np.array(coefficients)

# プロットの作成
plt.figure(figsize=(12, 8))

# 係数の変化をプロット
for i in range(coefficients.shape[1]):
    plt.plot(C_values, coefficients[:, i], label=f'Feature {i+1}')

plt.xscale('log')
plt.xlabel('C (inverse of regularization strength)')
plt.ylabel('Coefficient value')
plt.title('Coefficient values vs. C')
plt.axhline(0, color='black', lw=0.5)
plt.legend(loc='best', bbox_to_anchor=(1.05, 1), fontsize='small')
plt.grid(True)
plt.show()

図を確認した結果、$\lambda = 10^{-3}$から、$\lambda = 10^{-2}$への変化のあたりで、分類に重要な変数の回帰係数が0から1に変化していることがわかります。実際に選択されているのは、今回の例では $\lambda = 0.56$なので、少し細々とした特徴量も合わせて選択されてしまっていますが、まあそのあたりは仕方ないということでしょう。

最後に

複雑なモデルや手法もたくさんありますが、こういう基礎的なモデルの挙動をきちんと確認してみました。誰かの参考になれば幸いです。こういう方法について詳しく知りたいなと思った方は、スパース性に基づく機械学習がおすすめかなと思います。
https://shorturl.at/t1XpX