Polya-Gamma Thompson Sampling を実装する

元となる論文はこちら

PG-TS: Improved Thompson Sampling for Logistic Contextual Bandits
https://arxiv.org/abs/1805.07458

報酬が$\{0,1\}$の多腕バンディット問題における、Thompson Samplingがうまく機能することはよく知られた事実です。Thompson Sampling では、各アームに対する報酬の確率の事前分布に、ベータ分布 $Beta(\alpha,\beta)$ をおき各アームを引いた際の結果に応じて、成功なら $\alpha \rightarrow \alpha+1$とし、失敗なら $\beta \rightarrow \beta+1$と更新します。

Contextual Bandit においては、この報酬が文脈（個体の特徴量）に依存するため、各アーム$j \in \{1,2,...,K\}$に対する成功確率が
$$f_{j}(x)=\operatorname{sigmoid}(x^{\top}\theta_{j})$$
と表される問題となります。この問題に対して、Thompsonアルゴリズムを適用するためには、データが観測されたもとでの$\theta_j$の事後分布が必要です。しかし、残念なことに $\theta_j$の事後分布は陽に計算することができないため、MCMCを用いることになります。一方で、採択率の悪いMCMCを行いたくはないため、事後分布を2次近似したLaplace-TSが用いられていましたが、現実の問題における精度はあまり良いものではなかったという拝見があります。

そこで、この論文では、$\theta_j$ 事後分布からのサンプリングをPolya-Gamma 分布を使うことで非常に上手できるようにしようと考えています。この辺りの詳しい話は、Nospare の 小林先生の記事が非常にわかりやすいので、興味がある方はこちらを参照リンクとして置いておきます。

PG-TSの詳しい説明については、こちらが参考になりました。

実装

本当は特徴量が高次元の場合などを想定して、クラスタリングなども考えた方がいいのでしょうが、今回はとにかくnumpyだけでpolya-gammaも全部書くということにして、実装してみます。

import numpy as np
import math, random
import matplotlib.pyplot as plt
from IPython.display import clear_output

# =====================================================
# 1. Polya-Gamma(1, z) の無限級数展開サンプリング
# =====================================================
def sample_pg_1_z_series(z, K=200):
    """
    Polya-Gamma(1, z) を無限級数展開で打ち切り K項まで近似サンプリング。
    z は正負問わず、分布としては abs(z) で決まる。
    """
    z_ = abs(z)/2
    if z_ < 1e-12:
        z_ = 1e-12
    val = 0.0
    zpi = z_ / math.pi
    for k in range(1, K+1):
        # Gk ~ Exp(1)
        Gk = random.expovariate(1.0)
        denom = (k - 0.5)**2 + zpi*zpi
        val += Gk / denom
    val *= 0.5 / (math.pi**2)
    return val


def pg_sampler_one_iter(X, r, theta, lambda2=1.0, K=200):
    """
    Polya-Gamma ギブスサンプリングの 1ステップ:
      X: shape (n, d)
      r: shape (n,)  (0/1)
      theta: (d,)
      lambda2: 事前分散
      K: 無限級数打ち切り項数
    戻り値: 更新後の theta (1サンプル)
    """
    n, d = X.shape
    eta = X @ theta
    w = np.zeros(n)
    for i in range(n):
        w[i] = sample_pg_1_z_series(eta[i], K=K)
    z = (r - 0.5)/(w+1e-12)
    W = np.diag(w)
    prior_prec = (1.0/lambda2)*np.eye(d)

    XtW = X.T @ W
    post_prec = prior_prec + XtW @ X
    try:
        post_cov = np.linalg.inv(post_prec)
    except np.linalg.LinAlgError:
        post_cov = np.eye(d)*1e-12

    post_mean = post_cov @ (XtW @ z)
    new_theta = np.random.multivariate_normal(post_mean, post_cov)
    return new_theta

# =====================================================
# 2. ミニバッチ LogisticPGTS Agent
# =====================================================
class LogisticPGTSAgentMiniBatch:
    def __init__(self, d, K, lambda2=1.0, Kseries=200, update_freq=50):
        """
        d: 特徴次元
        K: アーム数
        lambda2: 事前分散
        Kseries: Polya-Gamma(1,z) サンプリング打ち切り項数
        update_freq: 何ステップごとに一括更新するか
        """
        self.d = d
        self.K = K
        self.lambda2 = lambda2
        self.Kseries = Kseries
        self.update_freq = update_freq
        
        # 各アームのデータセット
        self.X_list = [[] for _ in range(K)]
        self.r_list = [[] for _ in range(K)]
        # 推定パラメータ (MAP近辺 or 直近のギブスサンプル)
        self.theta_map = [np.zeros(d) for _ in range(K)]
        
        # ステップカウンタ
        self.t = 0
    
    def select_arm(self, x):
        """
        Thompson Sampling 的に:
          - 直近の推定 theta_map[k] に小さい分散を持つノイズを加えて
            x.dot( theta ) を計算、最大アームを選択。
        """
        sampled_values = []
        for k in range(self.K):
            # 小さい共分散から 1回サンプル
            cov_small = 0.01 * np.eye(self.d)
            theta_temp = np.random.multivariate_normal(self.theta_map[k], cov_small)
            score = theta_temp.dot(x)
            sampled_values.append(score)
        return np.argmax(sampled_values)
    
    def update(self, chosen_arm, x, r):
        """
        観測データ(x,r)を保存し、update_freq ごとに全アームを1回ギブス更新。
        """
        self.t += 1
        self.X_list[chosen_arm].append(x)
        self.r_list[chosen_arm].append(r)
        
        # ミニバッチ更新
        if self.t % self.update_freq == 0:
            # 全アームについて 1ステップ更新
            for k in range(self.K):
                Xk = np.array(self.X_list[k])
                rk = np.array(self.r_list[k])
                if len(rk) == 0:
                    continue
                new_theta = pg_sampler_one_iter(Xk, rk, self.theta_map[k],
                                                lambda2=self.lambda2,
                                                K=self.Kseries)
                self.theta_map[k] = new_theta
    
    def draw_posterior_samples(self, k, n_samples=1000):
        """
        (追加機能) アームkの最終データ (X_k, r_k) に対して
        Polya-Gammaギブスを n_samples ステップ回し、パラメータサンプルを取得。
        
        戻り値: shape (n_samples, d)
        """
        Xk = np.array(self.X_list[k])
        rk = np.array(self.r_list[k])
        if len(rk) == 0:
            return None  # 未観測アームの場合
        
        # thetaを直近値で初期化
        theta_current = self.theta_map[k].copy()
        samples = []
        for i in range(n_samples):
            theta_current = pg_sampler_one_iter(Xk, rk, theta_current,
                                                lambda2=self.lambda2,
                                                K=self.Kseries)
            samples.append(theta_current)
        return np.array(samples)

# =====================================================
# 3. Contextなし ThompsonSampling
# =====================================================
class ThompsonSamplingNoContext:
    def __init__(self, K):
        self.K = K
        self.alpha = np.ones(K)
        self.beta  = np.ones(K)
    
    def select_arm(self):
        samples = [np.random.beta(self.alpha[k], self.beta[k]) for k in range(self.K)]
        return np.argmax(samples)
    
    def update(self, arm, reward):
        if reward == 1:
            self.alpha[arm] += 1
        else:
            self.beta[arm] += 1

# =====================================================
# 4. シミュレーション
# =====================================================
def sigmoid(x):
    return 1./(1.+np.exp(-x))

def run_simulation(K=3, d=2, T=3000, seed=123, update_freq=50):
    """
    1) Contextなし (Bernoulli TS)
    2) ミニバッチLogisticPGTS
    
    K, d, T, update_freq を指定
    """
    np.random.seed(seed)
    random.seed(seed)

    # 真のパラメータ (K x d)
    true_theta = np.array([
        [ 2.0,  0.5],
        [-1.0,  1.5],
        [ 0.3,  2.0],
        [ 0,  1.0],
        [ -1.0,  0]
    ])
    # 必要に応じて K, d に合わせて拡張可能

    def generate_context():
        return np.random.rand(d)
    
    def get_reward(k, x):
        p = sigmoid(true_theta[k].dot(x))
        return 1 if np.random.rand() < p else 0
    
    def best_arm(x):
        vals = [sigmoid(true_theta[k].dot(x)) for k in range(K)]
        bk = np.argmax(vals)
        return bk, max(vals)

    # エージェント作成
    agent_nc = ThompsonSamplingNoContext(K)
    agent_mb = LogisticPGTSAgentMiniBatch(d=d, K=K, update_freq=update_freq)

    sum_r_nc  = 0.
    sum_r_mb  = 0.
    sum_reg_nc= 0.
    sum_reg_mb= 0.

    hist_r_nc = []
    hist_r_mb = []
    hist_reg_nc = []
    hist_reg_mb = []

    from IPython.display import clear_output

    for t in range(T):
        # 簡易プログレスバー
        if (t+1) % 500 == 0 or t==0:
            clear_output(wait=True)
            print(f"Simulation progress: {t+1}/{T} steps...")

        x_t = generate_context()
        best_k, best_val = best_arm(x_t)

        # 1) Contextなし TS
        arm_nc = agent_nc.select_arm()
        r_nc   = get_reward(arm_nc, x_t)
        agent_nc.update(arm_nc, r_nc)

        sum_r_nc += r_nc
        actual_val_nc = sigmoid(true_theta[arm_nc].dot(x_t))
        sum_reg_nc += (best_val - actual_val_nc)
        hist_r_nc.append(sum_r_nc/(t+1))
        hist_reg_nc.append(sum_reg_nc/(t+1))

        # 2) ミニバッチLogisticPGTS
        arm_mb = agent_mb.select_arm(x_t)
        r_mb   = get_reward(arm_mb, x_t)
        agent_mb.update(arm_mb, x_t, r_mb)

        sum_r_mb += r_mb
        actual_val_mb = sigmoid(true_theta[arm_mb].dot(x_t))
        sum_reg_mb += (best_val - actual_val_mb)
        hist_r_mb.append(sum_r_mb/(t+1))
        hist_reg_mb.append(sum_reg_mb/(t+1))

    return (agent_nc, agent_mb,
            hist_r_nc, hist_reg_nc,
            hist_r_mb, hist_reg_mb,
            true_theta)

# =====================================================
# 5. メイン: 実行 & 可視化
# =====================================================
def main():
    # パラメータ
    K=5; d=2; T=10000; update_freq=100

    (agent_nc, agent_mb,
     r_nc, reg_nc,
     r_mb, reg_mb,
     true_theta) = run_simulation(K=K, d=d, T=T, update_freq=update_freq)

    # 1) Reward & Regret の可視化
    plt.figure(figsize=(12,5))
    plt.subplot(1,2,1)
    plt.plot(r_nc, label='NoContext TS (Avg Reward)')
    plt.plot(r_mb, label='MiniBatch LogisticPGTS (Avg Reward)')
    plt.xlabel('Trial')
    plt.ylabel('Average Reward')
    plt.legend()
    plt.grid(True)

    plt.subplot(1,2,2)
    plt.plot(reg_nc, label='NoContext TS (Avg Regret)')
    plt.plot(reg_mb, label='MiniBatch LogisticPGTS (Avg Regret)')
    plt.xlabel('Trial')
    plt.ylabel('Average Regret')
    plt.legend()
    plt.grid(True)

    plt.tight_layout()
    plt.show()

    # 2) 最終的なパラメータの事後分布を可視化
    #   - アームごとに n_samples ステップのギブスチェーンを回して scatter/hist で表示
    n_samples = 100
    fig2, axes2 = plt.subplots(1, K, figsize=(5*K,4))
    if K==1:
        axes2 = [axes2]  # K=1の場合も反復可能に
    for k in range(K):
        samples_k = agent_mb.draw_posterior_samples(k, n_samples=n_samples)
        ax = axes2[k]
        if samples_k is None:
            ax.set_title(f"Arm {k}: no data")
            ax.axis('off')
            continue
        # d次元=2の場合を想定 => 2D scatter
        if samples_k.shape[1] == 2:
            ax.scatter(samples_k[:,0], samples_k[:,1], alpha=0.2, s=5)
            # 真の theta を表示
            tx, ty = true_theta[k,0], true_theta[k,1]
            ax.plot(tx, ty, 'r*', markersize=12, label='True Theta')
            ax.set_title(f"Arm {k} Posterior (2D scatter)\n[n={len(agent_mb.r_list[k])} data]")
            ax.legend()
        else:
            # d>2の場合: 1次元目だけヒストグラムなど工夫が必要
            ax.hist(samples_k[:,0], bins=30, alpha=0.5, label='Theta[0]')
            ax.hist(samples_k[:,1], bins=30, alpha=0.5, label='Theta[1]')
            ax.set_title(f"Arm {k} Posterior (d>2 partial plot)")
            ax.legend()
    plt.tight_layout()
    plt.show()

if __name__=='__main__':
    main()

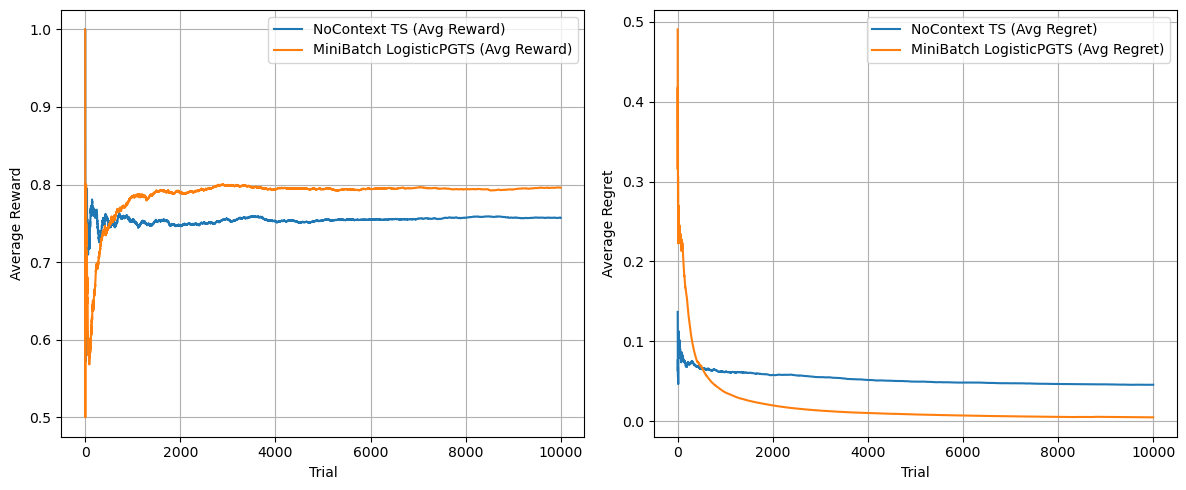
結果

比較的上手く結果が得られたのではないでしょうか...!!LogisticPGTS(PG-TS)は、本当は1回ずつパラメータを更新しようと思ったのですが、あまりにも重かったので Batchサイズ 100の minibatch更新を採用しています。事後分布からパラメータのサンプルも取ってみたものの、一番左以外はうまく行ってなさそうに思いますが、正直なところ報酬さえ最大化されれば良いので、いいのかなと思ったり（良くはない...）

まとめ

とりあえず、Polya-Gamma priorを用いて何かしたかったのと、今週末に何か話すネタが必要だったので、今回はPG-TSを実装して、動かした結果でお茶を濁そうと思います。（おわり）