モンテカルロ法を理解しやすいコードで書く

はじめに

初記事で拙いところがあると思いますが、ご容赦ください。
コードはGithubにあります。

実行環境

Python 3.8.5('base:'conda)
Anacondaの実行環境を導入している。

基本原理

N回シュミレーションを行ったときある事象がM回起これば、
その事象が起こる確率はM/Nで近似されるという性質を持っているということがモンテカルロ法の原理。

観測方法

1×1のXY平面上に原点から半径1の90度の弧を描いてランダムに点を打って
弧の外側と内側の点の個数の割合から円周率を求める。

コードの実装

monte1.rb

import random
import numpy
import time

start = time.time()

trial = 100
#試行回数
x = []
y = []
true = 0
false = 0
for i in range(trial):
    x.append(random.uniform(0, 1))
    y.append(random.uniform(0, 1))
    i = i+1

for i in range(trial):
    if numpy.sqrt(x[i]**2+y[i]**2) < 1:
        true = true+1
    elif numpy.sqrt(x[i]**2+y[i]**2) > 1:
        false = false+1

result = 4*(true/(true+false))

print(result)

elapsed_time = time.time() - start
print("elapsed_time:{0}".format(elapsed_time) + "[sec]")

試行回数を変えることによって精度が変化する。
また、出力までの実行時間を計測可能にする。

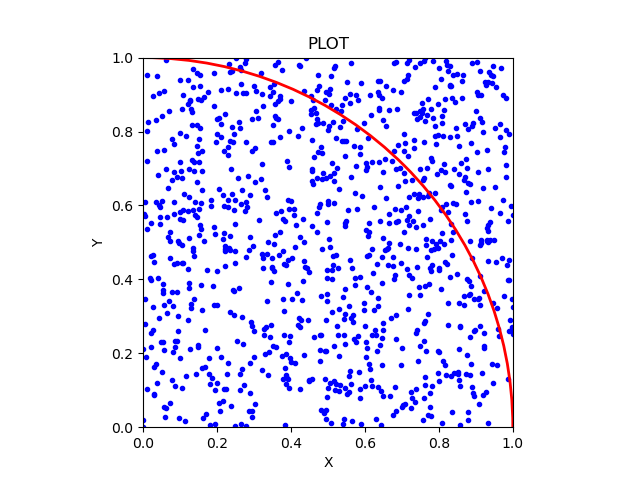
また、実際の図形を可視化してみる。

moten2.py

import random
import numpy
import matplotlib.pyplot as plt

trial = 10000
x = []
y = []
true = 0
false = 0
for i in range(trial):
    x.append(random.uniform(0, 1))
    y.append(random.uniform(0, 1))
    i = i+1

for i in range(trial):
    if numpy.sqrt(x[i]**2+y[i]**2) < 1:
        true = true+1
    elif numpy.sqrt(x[i]**2+y[i]**2) > 1:
        false = false+1

result = 4*(true/(true+false))

print(result)

c1 = plt.Circle((0, 0), radius=1, fc="None",
                ec="r", linewidth=2, color="black")
ax = plt.gca()
ax.add_patch(c1)
plt.axis("scaled")
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("PLOT")

plt.scatter(x, y, marker=".", color="blue", label="POINT")
plt.show()

実行結果

まとめ

試行回数を変えて何度か実行してみましたが、まだまだ結果が不安定。
試行回数を多くすればするほど実行時間が長いので今後は実行時間の短縮を目標としていきたい。