1行のPythonで＼(^o^)／を描く

はじめに

あるDiscordサーバーのbotで遊んでいたところ，コードをQiitaにまとめてほしいと言われたので，そのコードのうちの一つについて紹介と解説をしてみたいと思います．このような文章を書くのは初めてなので，表現の誤り等があれば指摘していただけるとありがたいです．

本題のコードと実行結果

早速，＼(^o^)／を描くコードを実行してみます．

owata.py

print("\n".join("".join(("0" if abs((i-30)**2+(j-7)**2-4)<2 or max(abs(j-abs(abs(i-30)-7)-1),j/5)<1 or abs((i-30)**2+5*(j-5)**2-300)<15 or abs(j+abs(i-30)-30)<1 else " ") for i in range(61)) for j in range(10)))

実行結果

0                0                         0                0
 0             0       0             0       0             0 
  0           0       0 0           0 0       0           0  
   0         0       0   0         0   0       0         0   
    0        0      0     0       0     0      0        0    
     0       0               000               0       0     
      0      0              0   0              0      0      
       0     0              0   0              0     0       
        0     0             0   0             0     0        
         0     0             000             0     0         

行間やフォントによって多少は見た目が変わったりしますが，＼(^o^)／を表示することができました．

コードの解説

なぜたったの1行で＼(^o^)／が描けるのかを，コードの重要な部分ごとに簡単な例を交えて解説していきます．

1行のコードでifを使う

三項演算子というものを使うと，条件分岐を1行で行うことができます．例えば，1001が13で割り切れるかどうかを出力するには次のようなコードが考えられます．

sample_if.py

 # 構文: 真の場合の処理 if 条件式 else 偽の場合の処理
print("1001は13で割り切れ" + ("る" if 1001%13==0 else "ない"))

実行結果

1001は13で割り切れる

1行のコードでforを使う

pythonにはリスト内包表記という記述法があり，これを用いることで改行することなく繰り返し処理を実装することが可能になります．例えば，0以上10未満の整数の3乗のリストを表示するには，次のように記述します．

sample_for1.py

 # 構文: [リストに入れる式 for 変数名 in 反復可能オブジェクト(rangeなど)]
 # range(10)はリストで表示すると[0, 1, 2, ..., 9]
print([i*i*i for i in range(10)])

実行結果

[0, 1, 8, 27, 64, 125, 216, 343, 512, 729]

また，次のように書けば多次元リストも作成することができます．

sample_for2.py

 # iは数値のリストを作るfor文の変数，
 # jはリストのリストを作るfor文の変数．
print([[i+j for i in range(4)] for j in range(4)])

実行結果

[[0, 1, 2, 3], [1, 2, 3, 4], [2, 3, 4, 5], [3, 4, 5, 6]]

文字列を結合する

最終的にはprint()関数で出力されるので，今回の場合は計算結果を1つの文字列にする必要があります．そこで，文字列メソッドのjoin()関数が役に立ちます．試しに，先ほど挙げた多次元リストのコードを文字列で出力するようにしてみましょう．この場合，リスト内包表記の[]は省略できます．

sample_for2_str.py

 # 構文: 結合に使用する文字列.join(文字列のリスト)
 # iによるリストは空白で，jによるリストは改行で結合する
print("\n".join(" ".join(str(i+j) for i in range(4)) for j in range(4)))

実行結果

0 1 2 3
1 2 3 4
2 3 4 5
3 4 5 6

これを利用すれば九九の表とかも作れそうですね．

＼(^o^)／の描画

ここまでが理解できれば，もう＼(^o^)／を描く準備は整いました．最初のコードを，今度は複数行で見てみましょう．

owata_indented.py

print(
  "\n".join(
    "".join(
      (
        "0" if
             abs((i-30)**2+(j-7)**2-4)<2
          or max(abs(j-abs(abs(i-30)-7)-1),j/5)<1
          or abs((i-30)**2+5*(j-5)**2-300)<15
          or abs(j+abs(i-30)-30)<1
        else " "
      ) for i in range(61)
    ) for j in range(10)
  )
)

i,jで適切な回数まで繰り返し，(i,j)の組それぞれについて三項演算子で"0"または空白を割り当て，それを結合して出力しています．三項演算子の条件式は，グラフで表すと下図の色を付けた部分(境界線は含まない)のようになります(desmosで描画，横軸がi，縦軸がj)．

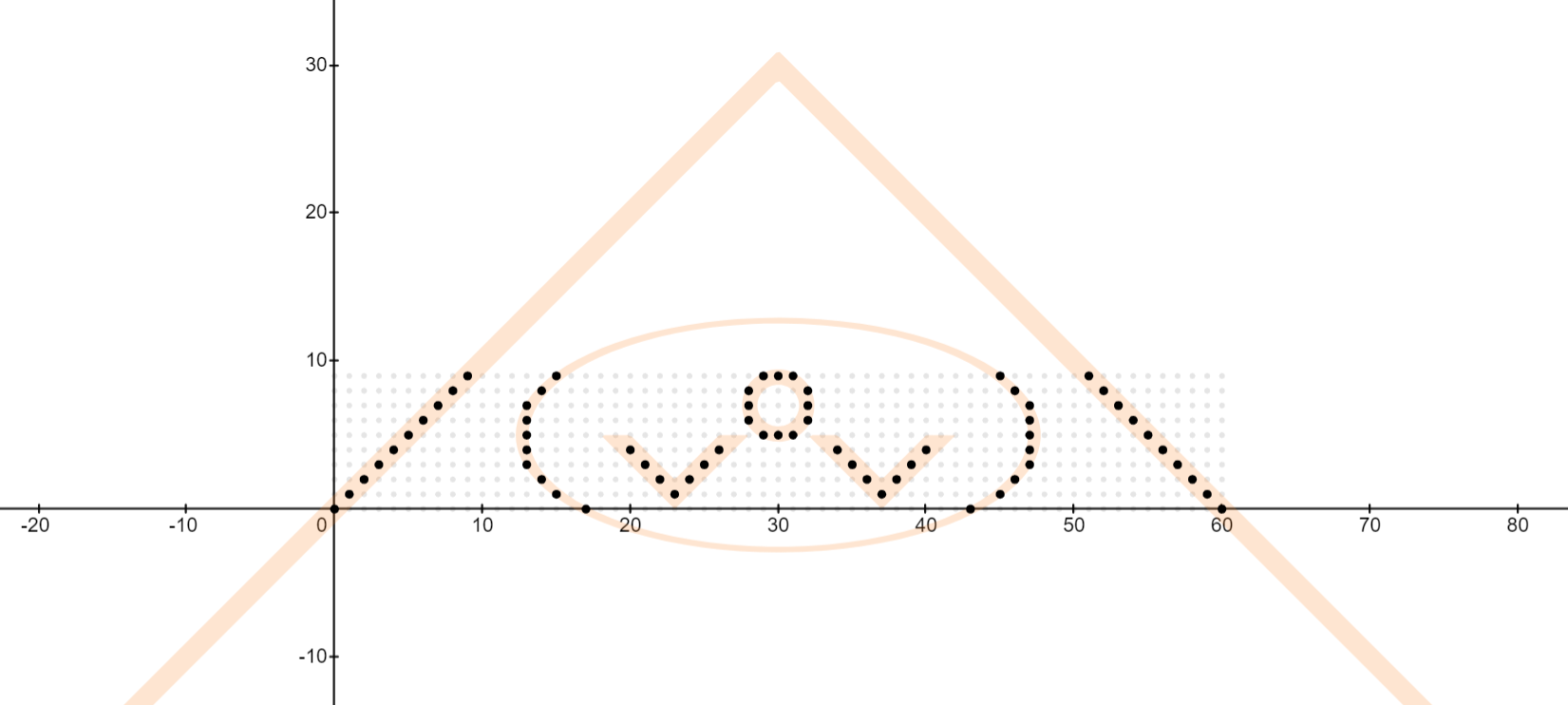
全ての点(i,j)を灰色の点で，そのなかで条件式を満たすものを黒色の点で表しています．詳しい式の部分は関数アートの領域で話し出すと長くなるため，今回は割愛させていただきます．ただ，いろんなグラフが一行で描けるんだなぁ，程度の認識で大丈夫です．あなたも円などの簡単なグラフから試していけば，すぐに絵を描けるようになれます(謎の勧誘)！

おわりに

Qiitaへの投稿は初めてでしたが，好きなことを書けて楽しかったです．Qiitaを勧めてくれたはにゃ氏に感謝しています．また気が向いたときに，他のコードについてもまとめていきたいと思います．