ABC138 C-Alchemistの問題
あなたは鍋とN個の具材を持っています。各具材は 価値 と呼ばれる実数の値を持ち、i個目の具材の価値はviです。2個の具材を鍋に入れると、それらは消滅して新たに1個の具材が生成されます。この新たな具材の価値は元の2個の具材の価値をx,yとして(x+y)/2であり、この具材を再び鍋に入れることもできます。この具材の合成をN−1回行うと、最後に1個の具材が残ります。この具材の価値として考えられる最大の値を求めてください。
解説PDF
コンテスト終了後にはコンテストページから解説PDF(YouTubeで解説動画も)を見ることができます。
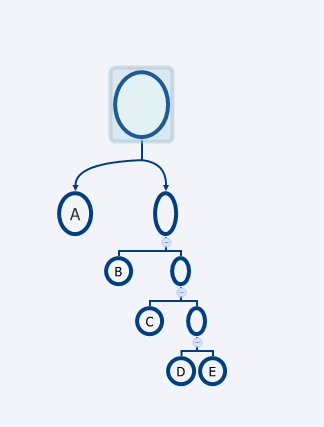
そこでは,以下のようなTree構造を考えると説明されていました(ただし,ここでは具材の価値についてA>B>C>D>Eとする)。
このTreeが表す手順はおよそ以下のようなもの
1.DとEを鍋にいれる。(D/2) + (E/2)の価値の新しい具材が生成される。
2.Cと1.で生成された具材を鍋に入れる。(C/2)+(D/4)+(E/4)の具材が生成される。
...
と繰り返すことで,最終的に残る具材の価値は(A/2)+(B/4)+(C/8)+(D/16)+(E/16)であり,これが取りうる価値の最大値である。
疑問
なぜ,この手順で価値が最大になるのでしょうか。
解説PDFでは,この手順が価値を最大にすることの説明は簡潔に
具材の番号を付け替えることで最終結果が向上するため
という程度の記載にとどまっていました(詳細は解説PDFを参照してください)。
※読む人が読めばすぐわかる程度には書いてあるのかもしれません
簡略な説明
先にもあげましたが,
具材の番号を付け替えることで最終結果が向上する
という記述や,YouTubeにあがっている解説動画でも触れられていましたが,考え方の方針は,ある手順(つまり,あるTree構造)を考えてそこにノードを付け足すときにどのように付け足すことが最善(価値を最大化する)かを考えれば良いと思います。
そこで,以下のようなTree構造を考えます。
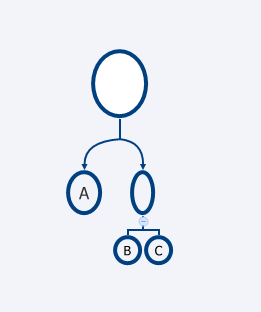
具材が3個のときに考えうるTreeの形はこの一つだけです。まず,このノードが3個のとき,価値が最大となるときを考えましょう。
この形のTreeの最終的な価値は(A/2)+(B/4)+(C/4)です。また,ノードA,B,Cを付け替えることで,最終的な価値を(A/4)+(B/2)+(C/4),(A/4)+(B/4)+(C/2)とすることもできます。
A>B>Cという条件の下で,この3つのうちどの値が最大でしょうか。
例えば以下のようにしましょう。
$\frac{A}{2}+\frac{B}{4}+\frac{C}{4}$ $\cdots①$
$\frac{A}{4}+\frac{B}{2}+\frac{C}{4}$ $\cdots②$
として,$\frac{①}{②}>1$となる条件を求めます。①,②に代入して計算すると,
$\frac{2A+B+C}{A+2B+C}>1$となり,さらに分母を払って整理すると$A>B$を得ます。
同様の計算により,A>B>Cという条件の下では,価値(A/2)+(B/4)+(C/4)が最大であることがわかります。
このTreeにあらたなノード(具材)Dを付け加えることを考えます。
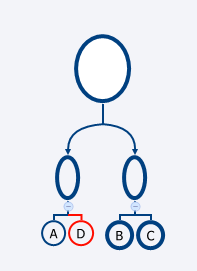
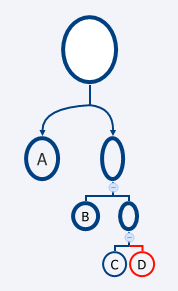
その場合に考えられるのはこの2通りのみです(A>B>Cは仮定します)。
1番目のTreeから得られる最終的な具材の価値は(A/4)+(B/4)+(C/4)+(D/4)。
2番目のTreeから得られる最終的な具材の価値は(A/2)+(B/4)+(C/8)+(D/8)。
となることがわかります。ここで,この2つの値を比較してみましょう。
$\frac{A}{2}+\frac{B}{4}+\frac{C}{8}+\frac{D}{8}$ $\cdots①$
$\frac{A}{4}+\frac{B}{4}+\frac{C}{4}+\frac{D}{4}$ $\cdots②$
として,さきほどのノードが3つのときと同様に$dfrac{①}{②}>1$ となる条件を考えます。
すると$A>\frac{C}{2}+\frac{D}{2}$を得ます。
これを$\frac{A}{2}+\frac{A}{2}>\frac{C}{2}+\frac{D}{2}$とみれば,A>Dである限り(A>B>Cは仮定されているので),右側のTreeが表す手順で得られる価値が最大となることがわかります。
もし,D>Aであれば,A,B,C,Dのうちから価値の大きい3つを選んで,その3つに対してラベルをA,B,Cと付け直せば同じ議論となります。
ノードがさらに増えても同じように考えることができます。
まとめ
簡単なパターン(ノードが少ないパターン)から考えて,ノードを付け足すということを考え,その際に価値が最大になる付け足し方はどのようなものかを考える。
また,大小関係によりラベルを付け替えることでうまく説明がつくというのは,実装上は最初にソートしておくことに相当します。