おさぼりハンドメイクZIP

この記事は eeic （東京大学工学部電気電子・電子情報工学科）その2 Advent Calendar 2018 16 日目の記事です．

はじめに

ファイル圧縮について調べていたら, 存外簡単そうなアルゴリズムで書かれていることを知ったので, 自分で実装してみるかーって記事です.

ファイル圧縮形式の中でも, 一番有名そうなzip形式に挑戦します.

アルゴリズム編で簡単にアルゴリズムを紹介し, 仕様編で実装しだすと気になってくる細かい仕様について説明します.
bitがうんたらみたいな話が嫌いな人は, 仕様編を飛ばしても大丈夫です.
次に, 結果編で圧縮ソフトと比較してみます.

アルゴリズム編

zip形式はDeflateと呼ばれるアルゴリズムを用いて圧縮を行います.

Deflateは以下の2つのアルゴリズムの組み合わせによって構成されます.

• LZSS
• ハフマン符号化

まず, LZSSによってファイルを圧縮し, さらにそのファイルをハフマン符号化によって圧縮して,
それを出力とします.
それぞれのアルゴリズムについて簡単に説明します.

※以下の説明では, 圧縮前の文書の最小単位を"文字", 圧縮後での最小単位を"符号"と表現しています.

LZSS

LZSSは辞書式圧縮法に分類されるアルゴリズムです.
辞書といっても別にテーブルを用意するのではなく, 圧縮対象の"文書自体"を辞書として使用します.
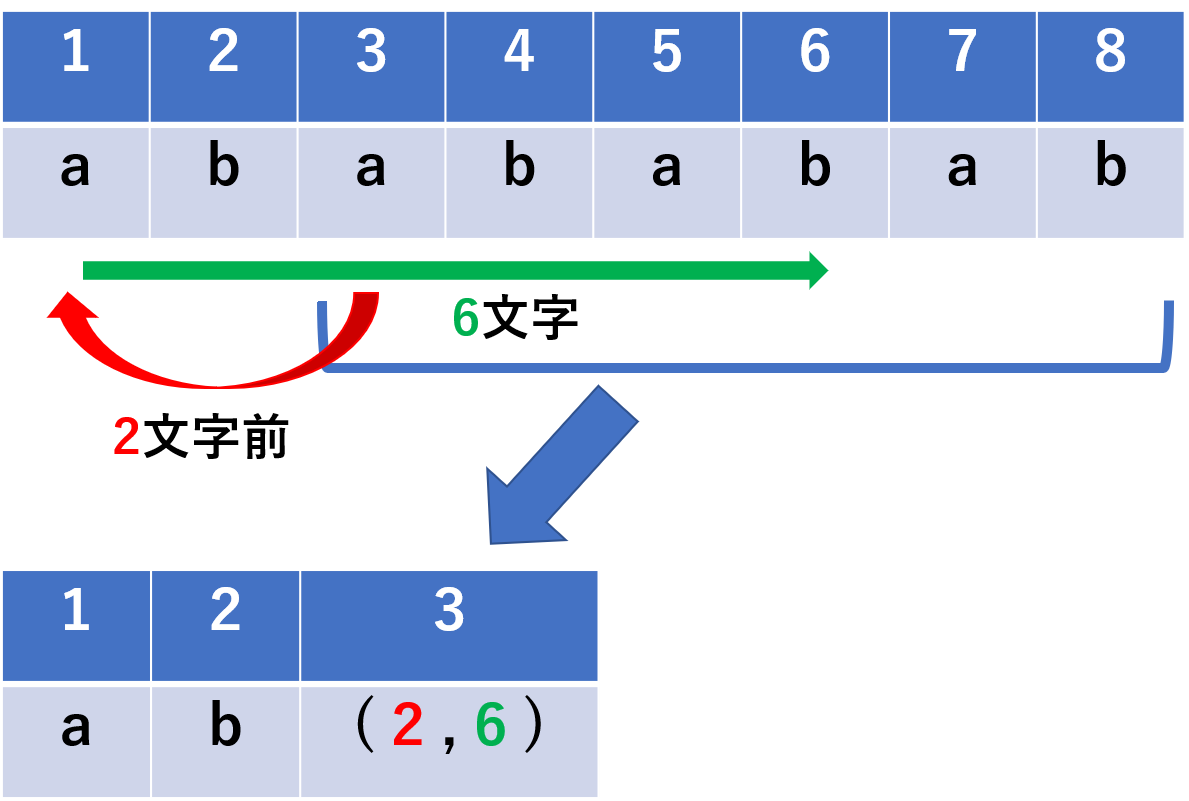
つまり, 圧縮対象の文字列に対して, テーブルから対応する符号を取得するのではなく, 直前までの文書内から一致する文字列を探索し, 出現箇所と文字長のペアという形で符号化します.
具体的な符号化の様子を下図に示します.

例1

例2

例1が一般的な符号化を表していますが, 繰り返しのある文字列は例2のように表すことができます.

これら図では省略していますが, それぞれの文字/符号の先頭に
圧縮しているか否かを表す1bitのflagを追加します
(以下, これを圧縮bitと呼びます).

ハフマン符号化

ハフマン符号化についてはこの教科書で散々やったと思うので,
ここでは, ハフマン木の正規化について説明します.

ハフマン符号化では, 出現頻度に応じて符号長を割り当てることが重要で, それぞれの符号自体が変化しても圧縮率に変化はありません.
なので, <文字, 符号長>のペアに対して任意のハフマン木を定義することができます.
冗長な情報を持たせないため(詳しくは後述)に, <文字, 符号長>のペアに以下の制約を課して, 単一のハフマン木しか構成できないようにします.

• 同じ符号長の文字は文字の昇順に並べる
• 木構造の深さを昇順に並べる

具体的なハフマン木の正規化を以下の図に示します.

例3

仕様編

この節では, アルゴリズム編で述べなかった実装の詳細について述べます.

LZSS

構成の最小単位(文字長)

だいたいのファイルはbitではなくbyteを最小単位として構成するので, 文字長を1byteに定めるのが自然です.
ですが, LZSSによって圧縮をすると無圧縮の場合でも前述した圧縮bitを付与することになります.
これにより, 最小単位が8bitから9bitになってしまい, めちゃくちゃ実装がめんどくさいです.

そこで, ターゲットを絞りすぎな気もしますが,
圧縮するファイルがASCII(7bit)で書かれていることを前提にします!

暴力的な解決策ですが, これで圧縮後も最小単位が8bitで扱うことができます.
(ASCIIは7bitですが, 上位bitは0埋めされて保存されています)

圧縮した符号のbit長

アルゴリズム編で, 文字列を出現箇所と文字長のペアに圧縮しましたが,　これらを表すbit長も考える必要があります.

文字長と同じく, 8bitの定数倍のサイズに収めたいので, テキトーに16bitと定めます.

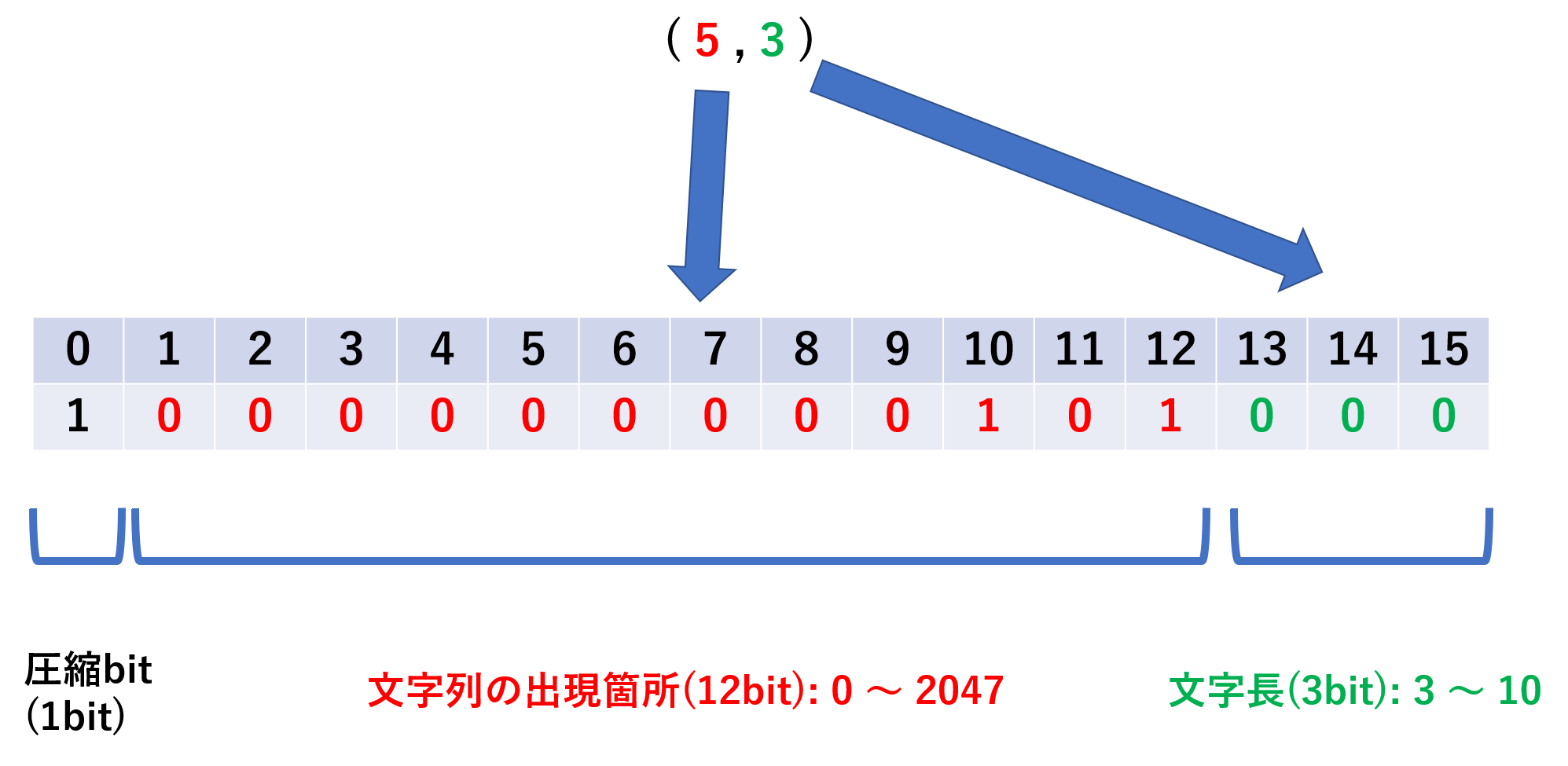
16bitの内, 先頭の1bitは圧縮bitとします.残った15bitを出現箇所と文字長に振り分けるわけですが, まあテキトーに(12bit,3bit)と振り分けます.

なので, 出現箇所は対象の文字から0～2047文字目まで, 文字長は0～7までとなります.

ここで, 文字長について少し考えます.
圧縮した符号は16bitになるので, 最低でも2文字以上は圧縮しないと, 圧縮することで符号長が長くなってしまいます.
なので, 文字長は3bitで3～10を表すことにします(b'000 → d'3, b'111 → d'10)

下図に例1で用いた値を実際のbitで表した図を示します.

例4

おさぼりじゃない実際のDeflateでは, (出現箇所, 文字長) = (16bit, 8bit)となっています.
文字長と1文字の長さ(ややこしい)が同じ8bitなのがコツです(後述).

ハフマン符号化

ハフマン木の伝搬

ハフマン符号化した文書を復元するには, 符号化で用いたハフマン木が必要です.
なので, 圧縮したファイルにハフマン木の情報も加えます.

出現した文字列のヒストグラムがわかれば, ハフマン木を構成することができますが,　出現頻度の上界を静的に定めることはできず, サイズが巨大になる可能性があります.

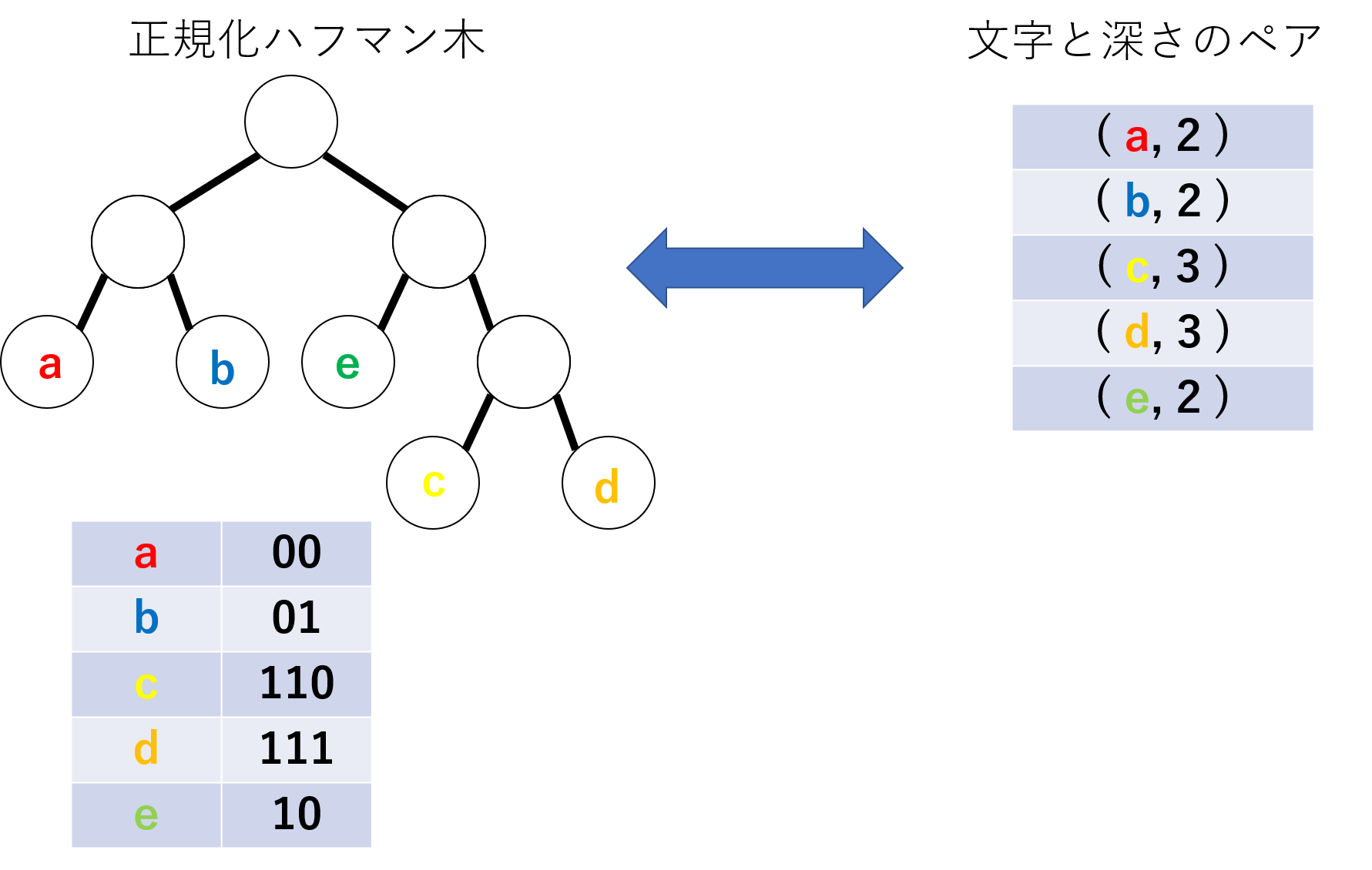
前述に説明したようにハフマン木を正規化することで, 文字と符号長のみでハフマン木を表すことができます.

下図に正規化ハフマン木と同値な文字と符号長のペアを示します.

例5

ヒストグラムでの出現頻度と異なり, 符号長はハフマン木に含まれる文字数を上界とするので, 簡単に定めることができます.

8bitの文字を対象とする場合は, 符号長も8bitで表します.

実際のDeflateでは, 静的に定めたハフマン木を使うモードもあり, その場合はハフマン木の情報を圧縮したファイルに付与しません.

ハフマン符号化の対象

LZSSによって, 無圧縮の文字と圧縮した符号が混在しています.
これらを同じハフマン木で符号化しても, 圧縮率は高くなりません.
なので, 複数のハフマン木によって圧縮を行います.
当然用いたハフマン木はすべて, 圧縮したファイルに記述することができます.

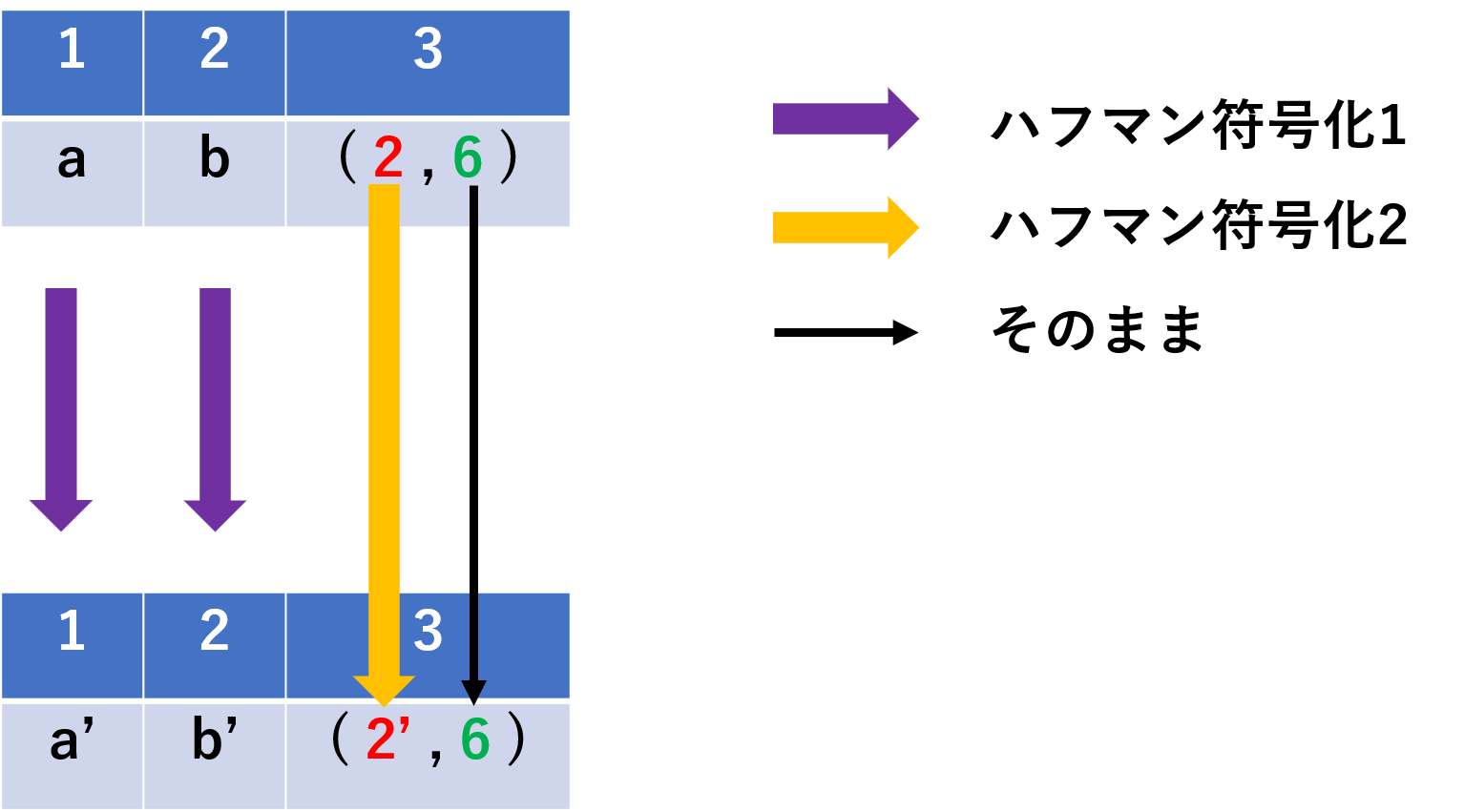
無圧縮の文字(7bit)と出現頻度(12bit)について, ハフマン符号化を行い, 圧縮bitと文字長(3bit)はハフマン符号化を行わないようにします.
下図に圧縮の様子を示します.

例6

ハフマン符号は瞬時復号可能なので, このように複数のハフマン符号/無圧縮の文字を混在させることができます.

実際のDeflateでは, 無圧縮の文字(8bit)と文字長(8bit)を同じハフマン符号で構成し, 出現頻度(16bit)はまた別のハフマン符号を構成します.

実際のDeflateでの圧縮の様子を下図に示します.

例7

結果編

今まで定めてきた仕様とアルゴリズムを用いて, 手作りZIPを実装したので,結果を見てみます.
コードはgithubにあげてます.
実装の苦労話とかも書こうかなって思ってたんですが,
ここまで書いて疲れた趣旨とずれそうなのでやめておきます.
別の記事で書くかもしれません.

ASCII専用にしてしまったので,
都合よくパソコンの中に入ってた英語論文を圧縮してみることにします.

結果1

 % ./comp paper.txt paper_origin                                                                                    
paper.txt size: 34716byte
after LZSS size: 15216byte
tree size: 164byte
tree size: 9078byte
not tree huffman size: 14431byte
after Huffman size: 23673byte

プログラムの第一引数が圧縮するファイル名(paper.txt)で
第二引数が圧縮したファイル名(paper_origin)です.

結果は上から

• 圧縮対象のファイルサイズ
• LZSSで圧縮した後のファイルサイズ
• 無圧縮の文字に関するハフマン木のサイズ
• 文字の出現箇所に関するハフマン木のサイズ
• ハフマン木のサイズを含まない圧縮した後のファイルサイズ
• ハフマン木のサイズを含む圧縮した後のファイルサイズ

となっています.

一番下の23673byteが最終的なファイルサイズです.
ハフマン木をファイル内に書くせいで, ハフマン符号化すると逆にサイズが増大してしまっています.

では, 本家の圧縮率を見てみましょう.

結果2

 % zip -r paper.zip paper.txt 
 adding: paper.txt (deflated 68%)                                                                                
 % ls -l | grep paper                                              
-rwxrwxrwx 1 root  34716 12月 15 23:31 paper.txt*
-rwxrwxrwx 1 root  22814 12月 16 00:00 paper.zip*
-rwxrwxrwx 1 root  15216 12月 16 00:24 paper_origin*

paper_originの値が結果1の一番下の値と違うのは,
ハフマン符号化(ハフマン木のサイズを含む)の圧縮率100%を超えると,
LZSSのみを適用するという小細工をしているからです.
かなり近いサイズまで, 圧縮できていることがわかります!
テキトーに設計した割には上々といったところでしょうか.

反省編

結果編で述べたように, ハフマン木をファイル内に書くことが大きいコストとなっています.
あらかじめ何種類かのハフマン木を用意して, 解凍の際にはそれを使用するということにして, ハフマン木に使ったサイズを除いて試算してみます.
14431 / 34716 = 0.415...　ということで約40%に圧縮できるということになります.
これならzipにドン勝できる!!!

この理想値で他の圧縮形式とも勝負してみます.

結果3

 % tar -zcvf paper.tar.gz paper.txt                                                                           
 paper.txt                                                                               
 % ls -l | grep paper
-rwxrwxrwx 1 root  11403 12月 16 00:03 paper.tar.gz*                                              
-rwxrwxrwx 1 root  34716 12月 15 23:31 paper.txt*
-rwxrwxrwx 1 root  22814 12月 16 00:00 paper.zip*
-rwxrwxrwx 1 root  15216 12月 16 00:24 paper_origin*

tar.gzにはボコボコにされました...

まあ, もっと重要な反省として, 圧縮のコードを書くのに疲れて解凍のコードは書けてません.
現時点で, 圧縮したバイナリは誰も解読できないゴミです.
解凍のコードも書けたら, githubにpushして, 別の記事で紹介したいなーと思います.

追記

解凍のコードも書けたので, 続きの記事を書きました.

appendix

デバッグの時に, バイナリ出力で便利だったコマンドを紹介します.

od

ファイルの中身をn進数で見ることができます.

% cat test1.txt
abcde
% od test1.txt
0000000 061141 062143 005145
0000006
 % od test1.txt -b                                                                                           
0000000 141 142 143 144 145 012
0000006

cout

16進数で見れます

std::cout << std::hex << std::showbase;
std::cout << 1216 << std::endl;
// 0x4c0 が出力される