正規分布がPowerPointで描画できればいいのに

TL;DR

• https://github.com/tomoaki0705/normalDistributionPPTX を公開したよ
• 下図のような正規分布曲線を、手書きしないでも「生成」できるよ

• この記事はOffice 365 Advent Calendar 2019の第4日目の記事です

背景

• きっかけは@a_hasimotoさんのツイートでした

パワポってなんで正規分布の曲線を引く機能がないんだろう．いつも使いたいと思うのだが．

— 橋本敦史 (@a_hasimoto) November 11, 2019

• また、去年公開した、キャリブレーションパターンを「生成」するツールの応用で行けると思い立ち、突貫工事で作りました。

リバースエンジニアリング

• pptxやxlsxみたいな、末尾にxがつく拡張子を持つオフィスのファイルは、その実体はZIPファイルです。
• pptxファイルの拡張子をZIPファイルにリネームしてファイルを展開すると、以下のようなxmlファイルの集合が現れます。

├─ ppt/
│   ├──presentation.xml
│   ├──presProps.xml
│   ├──slideLayouts/
│   ├──slideMasters/
│   ├──slides
│   │   └──slide1.xml <= こいつがスライドの本体
│   ├──theme/
│   ├──viewProps.xml
│   └──_rels/
├─ [Content_Types].xml
└─ _rels
    └──presProps.xml

• 裏を返すと、上記構成のディレクトリを「生成」し、ZIPで圧縮した上でリネームするとPPTXファイルを生成することができます
• ちょこちょこいじると分かるのですが、レイアウトやスライドマスタなど、特段編集する必要が無いファイルが多く含まれており、実際はppt/slides/slide1.xmlだけ適切に生成すれば、正規分布曲線を描けます。
• slides1.xmlファイルをいくつか生成すると、以下の様な構成であることが見えてきます。

<p:sp>
<p:nvSpPr>
<p:cNvPr id="2" name="qqqqqqqqq">
<a:extLst>
<a:ext uri="{FF2B5EF4-FFF2-40B4-BE49-F238E27FC236}">
<a16:creationId xmlns:a16="http://schemas.microsoft.com/office/drawing/2014/main" id="{29FFCF3D-8F32-482F-B193-ACC1CF50B0FA}"/>
</a:ext>
</a:extLst>
</p:cNvPr>
<p:cNvSpPr/>
<p:nvPr/>
</p:nvSpPr>
<p:spPr>
<a:xfrm>
<a:off x="2520000" y="1800000"/>
<a:ext cx="4320000" cy="3240000"/>
</a:xfrm>
<a:custGeom>
<a:avLst/>
<a:gdLst>
<a:gd name="connsiteX0" fmla="*/ 0 w 4320000"/>
<a:gd name="connsiteY0" fmla="*/ 3204006 h 3240000"/>
<a:gd name="connsiteX1" fmla="*/ 43200 w 4320000"/>
<a:gd name="connsiteY1" fmla="*/ 3196985 h 3240000"/>
:
</a:gdLst>
<a:ahLst/>
<a:cxnLst>
<a:cxn ang="0">
<a:pos x="connsiteX0" y="connsiteY0"/>
</a:cxn>
<a:cxn ang="0">
<a:pos x="connsiteX1" y="connsiteY1"/>
</a:cxn>
:
</a:cxnLst>
<a:rect l="l" t="t" r="r" b="b"/>
<a:pathLst>
<a:path w="4320000" h="3240000">
<a:moveTo>
<a:pt x="0" y="3204006"/>
</a:moveTo>
<a:cubicBezTo>
<a:pt x="14400" y="3201846"/>
<a:pt x="28800" y="3199516"/>
<a:pt x="43200" y="3196985"/>
</a:cubicBezTo>

• いきなりXMLの羅列なので面食らう読者もいるかも知れません。
• ちなみに、本物のxmlファイルは、改行なくぎっしり「1行」に詰めて記述されてますので、初心者お断りの見づらさです。¹
• 泥臭いリバースエンジニアリングをすっ飛ばして結論に行くと、**前半が「点の情報」、後半が「線の情報」**であることが分かります。

点

• 点の情報は特段不思議なことはありません。

<a:gdLst>
<a:gd name="X座標名0" fmla="*/ 点1のX座標 w X座標の最大値"/>
<a:gd name="Y座標名0" fmla="*/ 点1のY座標 h Y座標の最大値"/>
: 繰り返し
<a:cxn ang="0">
<a:pos x="点1のX座標名" y="点1のY座標名"/>
</a:cxn>

• このように、各点の座標は、座標ごと、そして座標の組み合わせで点が表現されています
• 同じスライド内で、「中央揃え」「右揃え」などで揃えた場合、同じ座標を再利用できるため、この様な構成になっていると推測します

線

• 問題は、点と点を結ぶ曲線の部分です。ここが正規分布曲線のキモです。
• なめらかな曲線を表現するためには、この中身を理解しないといけません。

<a:moveTo>
<a:pt x="0" y="3204006"/>
</a:moveTo>
<a:cubicBezTo>
<a:pt x="14400" y="3201846"/>
<a:pt x="28800" y="3199516"/>
<a:pt x="43200" y="3196985"/>
</a:cubicBezTo>

• 残念ながらこれだけ見ても、何のことだかさっぱりわかりません。
• 今度はPowerPointの画面からアプローチしてみます。

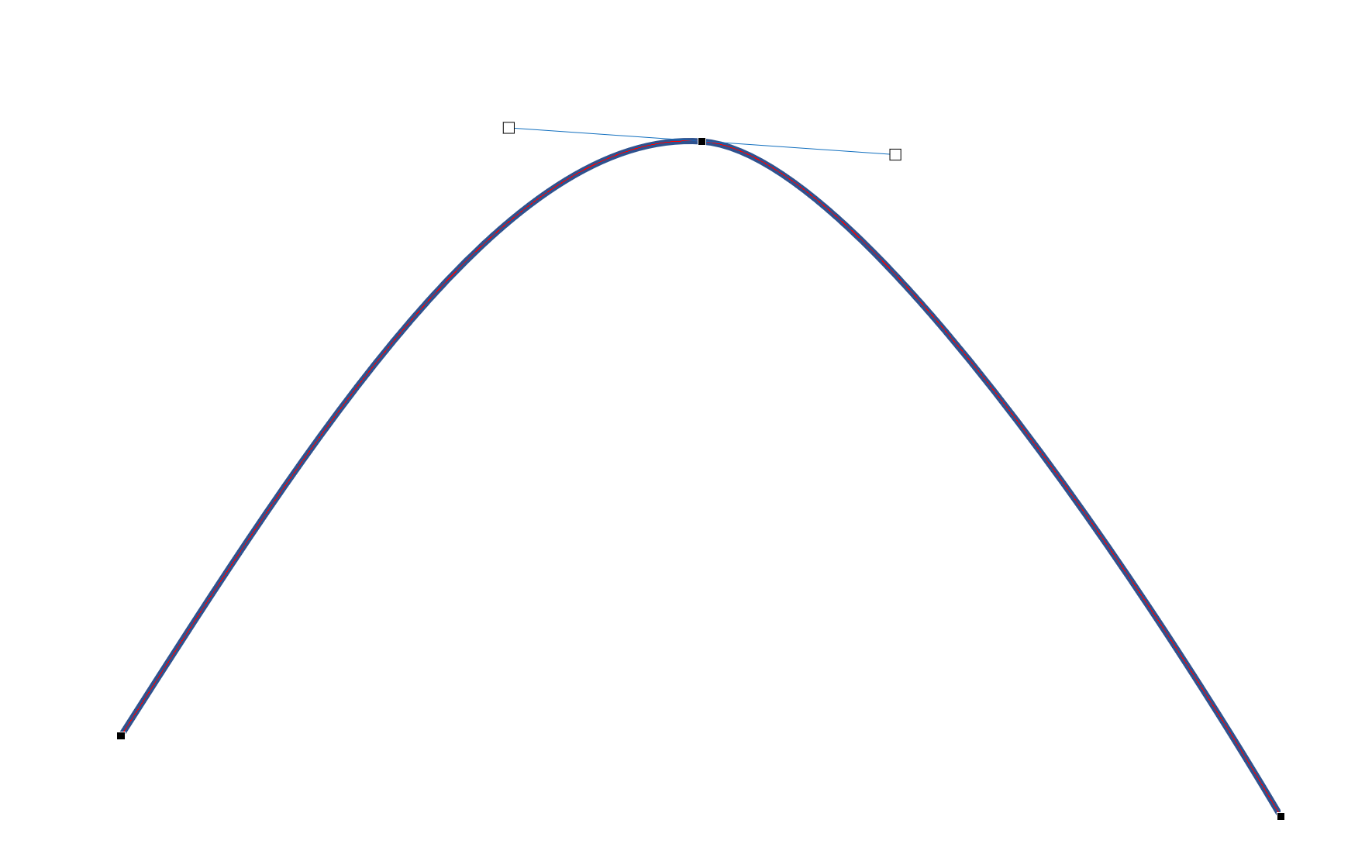
• 上図は、曲線を適当に書いた上で「頂点の編集」メニューを選んだ状態です。
• 3点で構成された曲線の、基準点をクリックすると、上図のように「接線っぽいもの」が表示されます
• また、先程のXMLをよく見て見ると cubicBezTo というキーワードがあり、「ベジエ曲線」っぽいキーワードが書かれています。
• ひょっとしてベジエ曲線で描かれてるのか？と推測してみました。

ベジエ曲線とは

• Wikipediaには以下のように書かれています。

ベジェ曲線（ベジェきょくせん、Bézier Curve）またはベジエ曲線とは、N 個の制御点から得られる N − 1 次曲線である。

• また、その特性として、

始点と第1制御点を結ぶ線分が始点における曲線の接線になり、第2制御点と終点を結ぶ線分が終点における曲線の接線になる

• と書いてあります。
• ということは、どうやら先程の
  • 「接線っぽいもの」はどうやら「接線」である
  • 接線を構成している点が、ベジエ曲線の制御点である
  • と推測できます。（探偵力発動）
• また、先程のベジエ曲線のパラメータとにらめっこしてみます

<a:gd name="connsiteX0" fmla="*/ 0 w 4320000"/>
<a:gd name="connsiteY0" fmla="*/ 3204006 h 3240000"/>
<a:gd name="connsiteX1" fmla="*/ 43200 w 4320000"/>   ＜====== 点1のX座標
<a:gd name="connsiteY1" fmla="*/ 3196985 h 3240000"/> ＜====== 点1のY座標
 : 中略
<a:cubicBezTo>
<a:pt x="14400" y="3201846"/>
<a:pt x="28800" y="3199516"/>
<a:pt x="43200" y="3196985"/>                         ＜=====＝ 点0と点1の間のベジエ曲線の制御点
</a:cubicBezTo>

• よく見ると、ベジエ曲線の制御点に3点記述されているのですが、3点目の座標は、終点の座標です。
• となると、点0と点1の間のベジエ曲線は

<a:cubicBezTo>
点0における接線
点1における接線
点1の座標
</a:cubicBezTo>

• で記述されていると推測できます。
• 実際にベジエ曲線の数は、点の数 - 1しか存在しないため、先程の記述と符合します

微分を計算するために

• ここまで来てようやくC++の出番です。
• 微分を計算する必要があるのですが、単純に「微小区間」を定め、その微小区間の「変化量」を計算します。
  • 微小区間がdx、変化量がdyに相当します。
• あとは機械的にグラフの描画区間で、正規分布曲線の座標と、各座標における接線の位置をひたすら出力していきます。

成果物

• 実行すると、と言いながらスクリプトに仕掛けがしてあるので、ビルド/makeするだけでpptxが生成されます
• ついでに、正規分布曲線に区間を表す色を付けたり、座標を付けたりしています
• また、$y = f(x)$ な曲線だけでなく、 $y = f(t), x = g(t)$ な曲線、つまり陰関数の曲線の描画にも対応しました
  • 1枚目のスライドに正規分布曲線、2枚目のスライドに対数螺旋が描かれます

顧客が本当に必要だったもの

• 本コードを公開し、ツイートで告知したところ、1000Favが付いて、今までのツイートで最もたくさんのイイねが付きました。
• しかし「イイね」した人の中で、実際clone/ダウンロードしてみた人はどれだけいるんだろうか。きっと誰も使ってないに違いない
• 多分、ビルドしたくないけれど、とにかく正規分布だけくれ、って人もいそうだったので、ビルド済みのpptxを公開しました。

The actual result that the customer wanted

• 別段無理にビルドしなくても適当な正規分布曲線を含んでおりますので、ご査収ください。
• 正規分布曲線の $0 < x$ なところだけほしいとか、$sin(x)$なグラフが書きたいという場合は、本ツールをちょこっと修正するだけでスライドが生成できますのでお試しください。

反省点

• 昨年の時から煽られている通り、python-pptx みたいな、C++でないツールを使うのが本当は美しいです。

python-pptxでpythonからpptx作れるのでよろしくおねがいします！

— Yusuke Uchida (@yu4u) February 20, 2019

• しかし個人的に移植のコストをかける気になれず。
• 誰かforkして公開してくれたりPRを書いてくれると嬉しいです。

1. XMLファイルをChromeに放り込むと、適切に整形して表示してくれるので、手っ取り早く確認されたい方はお試しあれ ↩