ハミング距離の計算はホントに速いのか？(ARM版)

はじめに

これは、OpenCV Advent Calendar 2016 6日目の記事です。関連記事は目次にまとめられています。
また、Computer Vision Advent Calendar 2013 でのwosugi氏のネタ ハミング距離の計算はほんとに速いのか？ の焼き直しでもあります

背景

• もとの記事でも書かれている通り、バイナリ特徴量において
• ハミング距離の計算そのものが速いのか
• バイナリ化の次元削減によって計算が速いのか
• が曖昧になっているというところからスタートしています。
• 2013年版はSSEを使って実験が行われ、結果L1（マンハッタン距離）がhammingが高速なのでは無く、次元数の削減が効果的という結果が出ました。
• 今回は、それをARMのNEONで試してみよう、という主題です

コード

• 基本的にはwosugi氏のコードを流用していますが、以下の点が違います

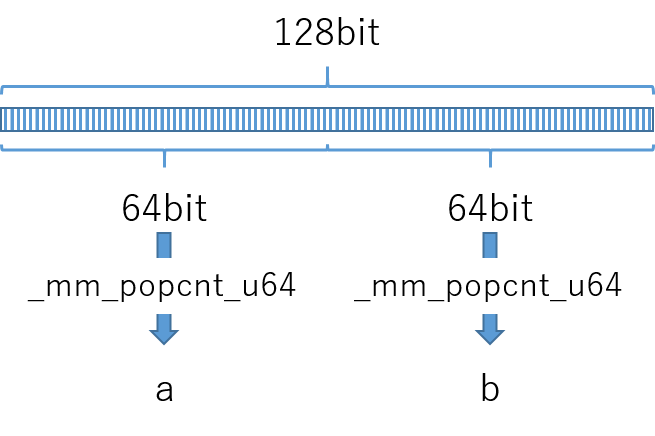
• NEONのpopcountとSSEのpopcountの違い

• SSEでは64bit長だが、NEONでは128bit長のデータを受け付けてくれるので、1回だけ128bit長のpopcount(VCNTQ)を実行する

• 同様に32bitごとのpopcountも、わざわざ32bit毎に分割するオーバーヘッドが生じ、効果がうすそうなので、今回は割愛

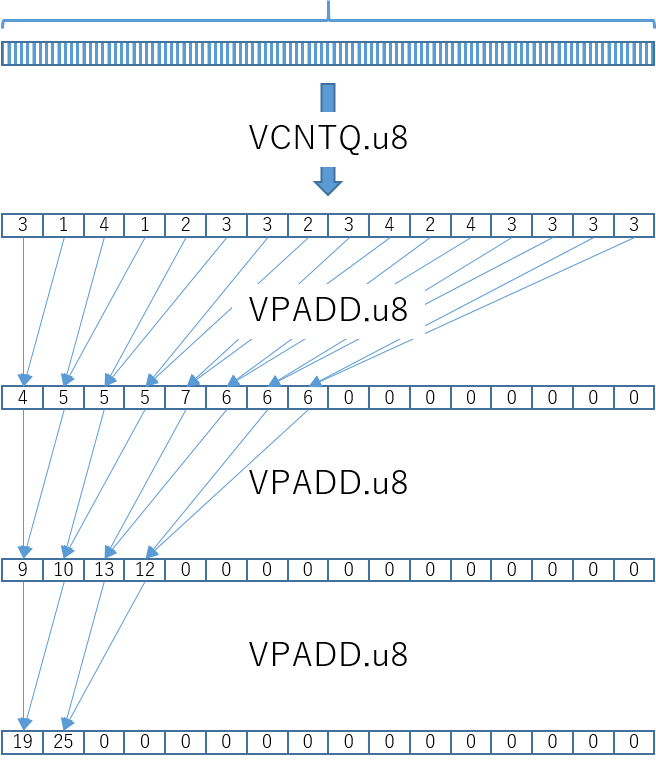
• SSEでは総和が帰ってくるが、NEONでは128bit内の、8bitごとのpopcount命令の結果として返ってくるので、reductionで総和を求める必要がある

• SSE によるpopcount はこんなイメージ
  

• NEON によるpopcount はこんなイメージ
  

• 全体のコードは[github] (https://github.com/tomoaki0705/benchmark-distance) に上げておきました

実行環境

• 以下のデバイスで実行してみました
• ODROID-C2 (Cortex A53、64bit Ubuntu、gcc 5.4.0)
• Raspberry Pi 3 (Cortex A53、32bit Raspbian、gcc 4.9.2)
• Jetson TK1 (Cortex A15、32bit Ubuntu、gcc 4.8.4)
• Jetson TX1 (Cortex A57、64bit Ubuntu、gcc 5.4.0)
• ODROID-X2 (Cortex A9、32bit Ubuntu、gcc 4.8.4)
• cmakeのオプションに-DCMAKE_BUILD_TYPE=release (O3相当)は付けないと辞書生成にアホみたいに時間がかかる

結果

• 以下のような実行結果になりました(単位はms)

method	platform	w/o SIMD	w/ SIMD
L2	Raspberry Pi 3	482	419
L2	Jetson TK1	431	393
L2	Jetson TX1	272	492
L2	ODROID-C2	556	927
L2	ODROID-X2	1022	852
L1	Raspberry Pi 3	443	275
L1	Jetson TK1	455	198
L1	Jetson TX1	335	153
L1	ODROID-C2	572	361
L1	ODROID-X2	842	536
hamming	Raspberry Pi 3	1254	279
hamming	Jetson TK1	1109	184
hamming	Jetson TX1	424	202
hamming	ODROID-C2	637	531
hamming	ODROID-X2	1916	566

• ボードごとの結果にまとめたのがこちら

platform	method	w/o SIMD	w/ SIMD
Raspberry Pi 3	L2	482	419
Raspberry Pi 3	L1	443	275
Raspberry Pi 3	hamming	1254	279
Jetson TK1	L2	431	393
Jetson TK1	L1	455	198
Jetson TK1	hamming	1109	184
Jetson TX1	L2	272	492
Jetson TX1	L1	335	153
Jetson TX1	hamming	424	202
ODROID-C2	L2	556	927
ODROID-C2	L1	572	361
ODROID-C2	hamming	637	531
ODROID-X2	L2	1022	852
ODROID-X2	L1	842	536
ODROID-X2	hamming	1916	566

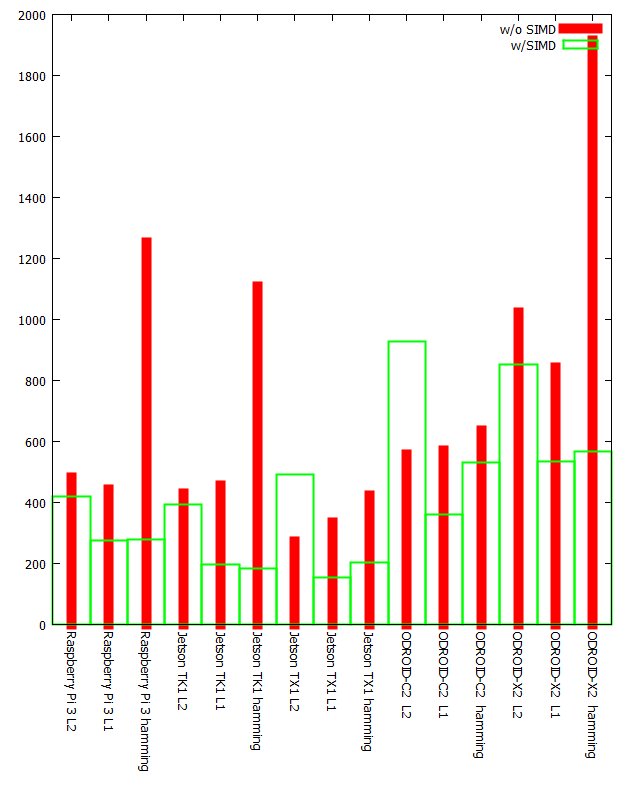
• グラフ化してみた

• 文字が潰れてるので、左からRaspberry Pi3のL2→L1→hamming、Jetson TK1、Jetson TX1、ODROID-C2、ODROID-X2の順
• 赤線がSIMD無し、緑色の箱型グラフがSIMDありの結果
• 縦軸は実行時間(ms)なので短いほど高速なことを表す

（追記）次元数での正規化

• ambee_whisperさんに指摘されましたが、この評価ではL1とL2は8bit/dimension、hammingでは1bit/dimensionであります
• つまり、time/dimension で比較するのがフェアではないかという指摘です
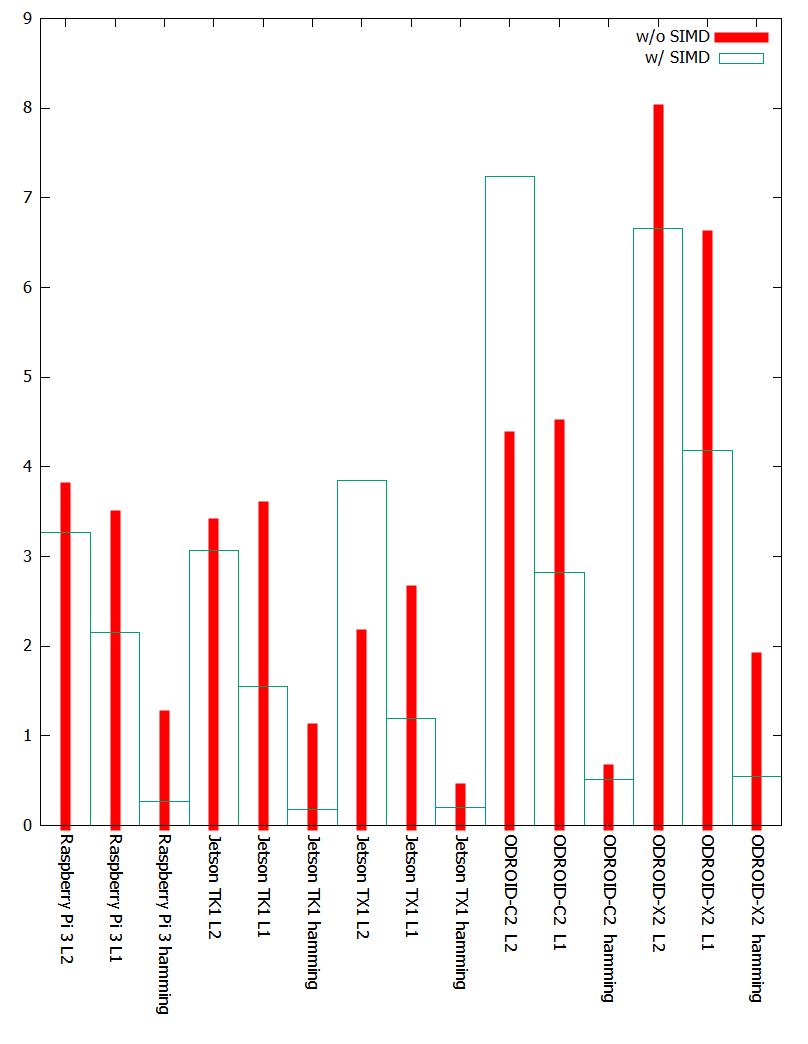
• ご指摘はもっともで、以下に結果をまとめた表を再掲。単位はms/dimension
• L2/L1は8bit/dimensionなので、128で割った値を、hammingは1024次元なので1024で割った値になっています

platform	method	w/o SIMD	w/ SIMD
Raspberry Pi 3	L2	3.765625	3.2734375
Raspberry Pi 3	L1	3.4609375	2.1484375
Raspberry Pi 3	hamming	1.224609375	0.272460938
Jetson TK1	L2	3.3671875	3.0703125
Jetson TK1	L1	3.5546875	1.546875
Jetson TK1	hamming	1.083007813	0.1796875
Jetson TX1	L2	2.125	3.84375
Jetson TX1	L1	2.6171875	1.1953125
Jetson TX1	hamming	0.4140625	0.197265625
ODROID-C2	L2	4.34375	7.2421875
ODROID-C2	L1	4.46875	2.8203125
ODROID-C2	hamming	0.622070313	0.518554688
ODROID-X2	L2	7.984375	6.65625
ODROID-X2	L1	6.578125	4.1875
ODROID-X2	hamming	1.87109375	0.552734375

• 文字が潰れてるので、左からRaspberry Pi3のL2→L1→hamming、Jetson TK1、Jetson TX1、ODROID-C2、ODROID-X2の順
• 赤線がSIMD無し、緑色の箱型グラフがSIMDありの結果

結果を眺めて見て（もろもろ追記/削除）

• 概ね、SSE版と似た傾向が出ています。ただ、正規化した結果はhamming圧勝です。
  • hammingとL1の計算時間自体はかなり接戦なのですが、hammingは8倍の次元数を扱ってるので、結果hammingの圧勝です
• しかし、よく見ると32bit OSが乗ったARMではhammingが最速、もしくはL1と接戦を繰り広げています
• Raspberry Pi 3 275ms(L1) VS 279ms(hamming)
• Jetson TK1 198ms(L1) VS 184ms(hamming)
• ODROID-X2 536ms(L1) VS 566ms(hamming)
• こちらのボードはいずれもも32bit OSです。(Raspberry Pi 3 のCortex A53は64bit対応だが、OSのRaspbianは32bit)
• hammingも、L1でも、結果は8bit単位16要素で返ってくるので、総和を求めるためにreductionの必要があり、そこのコストはhammingもL1も同等に思えます
• とすると、ARMの popcount(VCNTQ)命令はabs diff(ABDQ)命令と同等のスループットを持っているのかもしれません
• 32bit OSではSIMD無し版のhammingが異様に遅く、SIMD化して一気に高速化されているのも気になります
• ここの実装はx86向けのコードそのまま流用なので、SIMD無しの書き方はもう少し工夫の余地がありそうです
• 64bit OS上でのL2距離がなんとSIMD無しの方が速いという屈辱
• Jetson TX1 272ms(SIMD無し) VS 492ms (SIMDあり)
• ODROID-C2 556ms(SIMD無し) VS 927ms (SIMDあり)
• 馬鹿な！オートベクタライズの方が高速だとっ！？
• 結構屈辱。さらっとアセンブリを眺めた感じ、ループアンロールされていて、それが効いている様にも見える。
• しかし細かい検証はしてません
• Jetson TX1、ODROID-C2、ともにL1の方が高速です。
• 64bit OSでの結果は、L1の方がhammingより有意な差を持って高速な結果となりました(SSEと同様の傾向)
• ここが最大の謎。Raspberry Pi 3はCortex A53上で動いているので、決して64bit ARMが遅いという訳ではなく、64bit OSで実行するとhammingとL1に有意な差が現れます
• そのうち64bit のRaspbian とかが出たら（もう出てる？）32bit/64bitの比較とかしてみると面白いかもしれません（そこまで手が回りませんでした）
• 64bit でも、ms/dimensionの結果ではhamming が最速となりました
• なお、各CPUはベースクロックもマチマチなので、ボード間の比較は余り意味が無いと思います

OpenCVでの使い方

• これだけだとOpenCV advent calendar にOpenCV抜きな記事を書いてしまうので、OpenCVにまつわる情報を何か書いておきましょう
• OpenCVには、cv::normHammingというHamming距離を求めてくれる関数があります

stat.cpp

int normHamming(const uchar* a, int n)
{
    int i = 0;
    int result = 0;
#if CV_NEON
    {
        uint32x4_t bits = vmovq_n_u32(0);
        for (; i <= n - 16; i += 16) {
            uint8x16_t A_vec = vld1q_u8 (a + i);
            uint8x16_t bitsSet = vcntq_u8 (A_vec);
            uint16x8_t bitSet8 = vpaddlq_u8 (bitsSet);
            uint32x4_t bitSet4 = vpaddlq_u16 (bitSet8);
            bits = vaddq_u32(bits, bitSet4);
        }
        uint64x2_t bitSet2 = vpaddlq_u32 (bits);
        result = vgetq_lane_s32 (vreinterpretq_s32_u64(bitSet2),0);
        result += vgetq_lane_s32 (vreinterpretq_s32_u64(bitSet2),2);
    }
#elif CV_AVX2
    {
        __m256i _r0 = _mm256_setzero_si256();
        __m256i _0 = _mm256_setzero_si256();
        __m256i _popcnt_table = _mm256_setr_epi8(0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
                                                 0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4);
        __m256i _popcnt_mask = _mm256_set1_epi8(0x0F);

        for(; i <= n - 32; i+= 32)
        {
            __m256i _a0 = _mm256_loadu_si256((const __m256i*)(a + i));

            __m256i _popc0 = _mm256_shuffle_epi8(_popcnt_table, _mm256_and_si256(_a0, _popcnt_mask));
            __m256i _popc1 = _mm256_shuffle_epi8(_popcnt_table,
                             _mm256_and_si256(_mm256_srli_epi16(_a0, 4), _popcnt_mask));

            _r0 = _mm256_add_epi32(_r0, _mm256_sad_epu8(_0, _mm256_add_epi8(_popc0, _popc1)));
        }
        _r0 = _mm256_add_epi32(_r0, _mm256_shuffle_epi32(_r0, 2));
        result = _mm256_extract_epi32_(_mm256_add_epi32(_r0, _mm256_permute2x128_si256(_r0, _r0, 1)), 0);
    }
#endif
    for( ; i <= n - 4; i += 4 )
        result += popCountTable[a[i]] + popCountTable[a[i+1]] +
        popCountTable[a[i+2]] + popCountTable[a[i+3]];
    for( ; i < n; i++ )
        result += popCountTable[a[i]];
    return result;
}

• 内部的には、CV_NEONとCV_AVX2の場合があります。
• [昨日書いたUniversal Intrinsics] (http://qiita.com/tomoaki_teshima/items/8195c25a3f0448ce300b) が使われてないので、PRチャンスであることに今気が付きました。ふむふむ
• と思ってPRに着手したものの、Universal IntrinsicはSSE2までの縛りプレイな上に、popcountはSSE4.2以降の対応なので、相当な縛りプレイに。
• 誰得なPRになりそうですが、どうしたものか
• そもそも、x86では、AVX2でしかintrinsicが使われてないので、AVXまでしか対応してない私のMBPだとそもそもSIMDの恩恵を受けられないとは！
• がっかりです。。。
• (追記:)がっかりするだけでなく、SSE2でpopcountしたPRを投げてみました
• (追記:)願わくば3.2のリリースに含まれれば、と思ったのですが、RCが出た後は新規機能追加のマージはしてくれないようで、あっさり3.2には含めてもらえませんでした。
• (追記:)PRから一ヶ月経って、ようやくマージされました！。結局SSE2版とSSE4.1版をcommitしました

おわりに

• 先日ばったり、wosugi氏にお会いして、たまたまこのpopcountの話で盛り上がったので、Advent Calendar に仕立て上げてみました。
• 32bit版のARMではhamming距離はL1距離と同等の性能を示しますが、64bit版ではまだL1に分があるようです。
• 32bit版のARMでは計算時間自体はL1とhammingとで同等の性能を示しますが、正規化した結果では32bit版/64bit版のARMともにhamming圧勝でした。
• popcountに幸あれ
• NEONとSSEを総じて見ると、_mm_popcnt_u64だけがイケてない、という気がする。
• 明日はTaroYamada さんの記事です。お楽しみに！

補足

• OpenCV (git版リビジョンecb8fb964d)
• ARMのボードの詳細は文中に