統計モデリングとは
今回は「統計モデリング」という考え方を解説します。と言っても別にこれは新しい概念ではありません。
統計モデリングとは、既存のデータにその背後にあるプロセスを仮定することで、そのプロセスの中のパラメータを推定しようとする手続きです。
例えば、線形回帰も統計モデリングの一種とみなすこともできるでしょう。変数XとYの間に、
Y = aX + B + \varepsilon
という仮定をおいて線形回帰をするとき、$a,b$、そして$\varepsilon \sim N(0,\sigma)$の$\sigma$というパラメータを推定しようとしています。
さらっと書きましたが、実は伝統的な統計学の枠組みでは、線形回帰の誤差項$\varepsilon$には正規分布を仮定していました。もし何かの強い信念や事前知識により、誤差項の分布が正規分布でないと思う場合、単純な線形回帰を実行することは適切ではありません。そういった「拡張」にも対応することができるのが統計モデリングです。
しかし、統計モデリングの一番の強みは、より複雑なデータの生成プロセスを仮定することができることです。これはこの後の実例で見ます。
最後にもう一つ、伝統的な統計学と統計モデリングの違いに触れておきます。統計モデリングはベイズ統計という考え方に基づいています。そこから生まれる大きな違いは何かというと、伝統的な統計学がパラメータの真の値を点推定しようとしていた一方、ベイズ統計ではパラメータに「真の値」などなく、パラメータも分布を持っていると考え、その分布を推定することを目的とします。
しかし実際問題、最後は推定されたパラメータの分布の代表値(たとえば平均値)で解釈すればよいので、この違いを大きく意識する必要はありません。
統計モデリングの実例 - Jリーグにホームアドバンテージは存在するか
上の説明でけでは統計モデリングがどう使えるのかがさっぱりわからないので、実例で解説します。
今回解きたい問題は、「Jリーグにホームアドバンテージが存在するか」です。
サッカーに詳しくない方のために説明すると、サッカー(スポーツ全般)では一般的にホームチームが有利だと言われています。これはファンによる応援や、環境への慣れ、移動による時差などが原因だと考えられています。
しかし、Jリーグのファンは海外に比べると比較的穏やかであり、環境や時差の違いも少ない日本国内においてこれらの要素が強く影響するとは思えません。
そこで、これを検証し、定量化しようというのが今回の目的です。
今回は2019年のJ1リーグの結果を使います。
シンプルなアプローチ
この問題に対して一番簡単なアプローチは、簡単な統計を取ってみることではないでしょうか。
すると、2019年のJリーグではホームチームの128勝106敗72分、という極めて微妙な結果が得られました。
$\chi^2$検定という統計検定をしてみたところ、$p=0.12$というホームチームが有利とは言い切れないという結果を得ました。
統計モデリングのアプローチ
では、次に統計モデリングをしてみましょう。これには、試合の勝ち負けが決まるプロセスを仮定する必要があります。そこで、以下のようなプロセスを考えます。
各チームは固有の「強さ」$\mu_i$と「勝負ムラ」$\sigma_i>0$を持っています。$\mu_i$が大きいほど平均的に強いチームで、$\sigma_i$が大きいほど試合ごとに強さが変わりやすいチームです。
ある試合において、ホームチーム$h$とアウェイチーム$a$が対戦する時、両チームの「パフォーマンス」$p$は、
\begin{align}
p_h =& \mu_h + \varepsilon_h + adv \\
p_a =& \mu_a + \varepsilon_a
\end{align}
で得られるものとします。ただし$\varepsilon$は試合ごとのパフォーマンスのムラを表し、$\varepsilon_i \sim N(0, \sigma_i)$とします。何を言っているかというと、各チームの試合でのパフォーマンスは、平均的な強さに正規分布のムラがのり、さらにホームチームはホームアドバンテージを得ます。
そして試合結果は、$p_h-p_a>1$のとき、ホームチームの勝ち。$p_a-p_h>1$のときアウェイチームの勝ち。それ以外では引き分けとします。つまり、パフォーマンスに差が1以上つけば勝ち、そうでなければ引き分けになるものとします。
(これだけだと強さの基準が一意に定まらないため、$\mu \sim N(0, \sigma_\mu)$つまり強さの平均は0という仮定もおきますが、本質的ではありません)
プロセスの仮定は以上です。色々なパラメーターを仮定しましたが、観測可能なのは試合結果だけであることに注意してください。$\mu_i, \sigma_i, adv$が求めるべきパラメータです。
上のモデルからパラメータを求めるにはいろいろなソフトウェアがありますが、今回はstanというものを使いました。実は上のモデルにはStanとRでベイズ統計モデリングという本にあった、将棋棋士の強さの推定を参考にしています。わかりやすい本なので、実装の方法はこちらの本をご覧ください。
まずは、強さ$\mu$の推定結果です。平均値の大きい順に並べてあります。
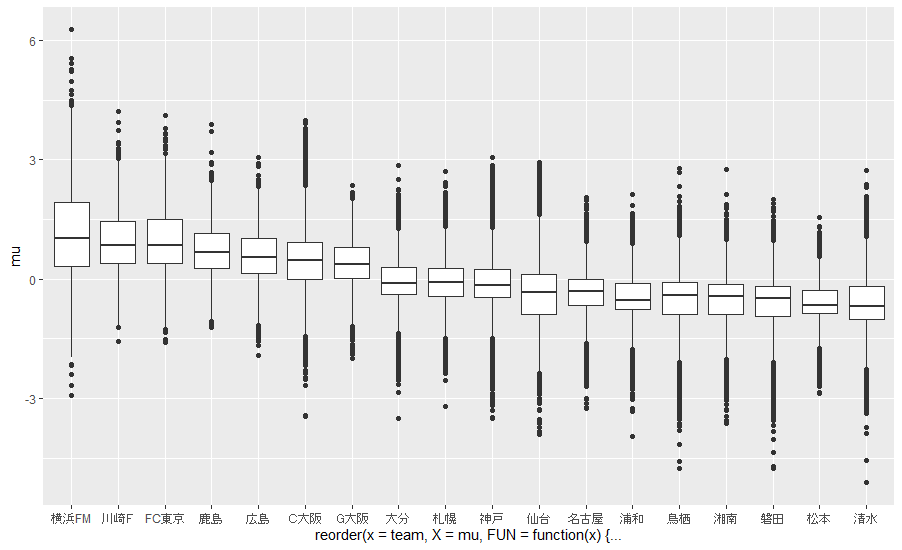
分布の裾野がかなり広くなってはいますが、この順番はかなり説得力があるのではないでしょうか。
と言ってもサッカーを見ない人には意味不明かと思いますので、実際の順位との比較表を張ります。
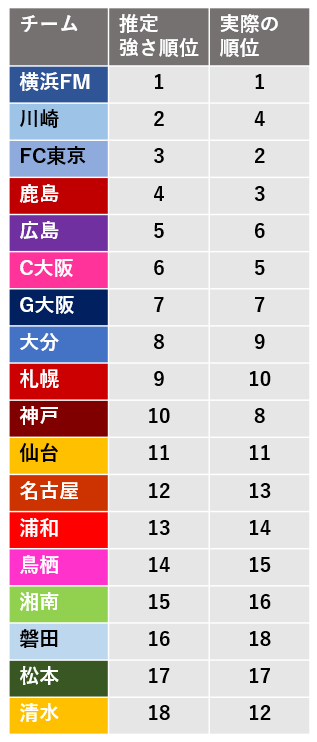
上位のチームほど、強く推定されています。そのため、このモデルは完全な嘘ではなく、何かしらの現実を映していると言えるのではないでしょうか。
ホームアドバンテージを推定してみましょう。$adv$の推定値の平均は0.43となりました。
横浜FMの強さの推定値は1.11、清水は-0.63であり、全部で18チームあるため、平均的には強さ0.1の差が順位ひとつの差であると考えられます。
なので、J1には平均的には順位4つ分上になる程度のホームアドバンテージがあると推定できました。4つ分というのは、大きすぎないがまったくゼロでもない絶妙な大きさで、肌感覚にも合致しているのではないでしょうか。
まとめ
以上、今回は統計モデリングという手法を紹介しました。
統計モデリングの弱点は、あるモデルを仮定するととりあえず何らかの推定値が得られてしまう点にあります。ですので、その結果を解釈して、仮定したモデルが現実を反映できているかどうかを確認する必要があります。
また、今回の記事を書く上でJのリーグの試合結果モデルを作りましたが、不等式条件の実装にとても苦労しました笑。日本語で(英語でも)解説されたリソースが他の分野に比べて圧倒的に少ないため、実装には試行錯誤が必要かもしれません。