今回のテーマ
今回は機械学習のアルゴリズムや手法ではなく、作成したモデルをどう評価し、どう選ぶかについてお話しします。
モデルの評価 - モデルの「よさ」の測り方
あなたはあるデータ、例えば前回の大学受験のデータを1万人分もっていたとしましょう。そのデータをすべて何らかのアルゴリズム(ロジスティック回帰など)に入れて、あるモデルを得ました。そのモデルは1万人中9900人の合否を正しく予測しました(精度99%)。はたしてこのモデルは精度99%の素晴らしいモデルだと言ってよいのでしょうか?
と、いうのがこの節で述べる話です。
実は上記のプロセスには、大きく分けて2つの問題があります。一つが__in-sample__の精度と__out-of-sample__の精度は必ずしも一致しないという問題。もう一つがそもそも「精度」がモデルの良さを表す指標とは限らないという問題です。
トレーニングデータとテストデータ
機械学習は持っているデータ(in-sample)の中にパターンを見つけ、そのパターンを「まだ見ぬデータ」(out-of-sample)に当てはめて何かを予測しようとします。しかし、あるデータの中に見つかったパターンが他のデータにも適用できる、ということは機械学習のアルゴリズムそのものによって保証されていません。これは実は我々が勝手に__思い込んでいる__だけです。
しかし、それではモデルをビジネスや実生活に適用することは不安で仕方がありません。ではどのように「あるモデルが汎用性を持つ」ということを確認するのでしょうか。
そのために使われるのが__トレーニング(訓練用)データ__と__テストデータ__という概念です。
簡単に言うと、持っているデータの一部を精度確認用に取っておくのがテストデータで、残りのトレーニングデータを使ってモデルを作成します。
モデル作成の手続きを順を追って説明します。
まず初めにデータをそろえたら、ランダムに20%程度をテストデータとして切り分けます。このテストデータは最後に精度を確認するまで二度と触ってはいけません。
残りの80%を使ってモデルを作ります。例えば、ロジスティック回帰に突っ込みます。
結果のモデルを使って、テストデータを予測してみます。そして精度がどれだけであるかを確認します。この__テストデータに対する精度がこのモデルの精度__です。
テストデータに触ってはいけないというのはどういうことでしょうか。これは読んで字のごとくなのですが、それでも違反する人が後を絶ちません。
たとえば、多くの変数があるデータを考えましょう。あなたは多重共線性を嫌がってデータの各変数ごとの相関を見たくなるかもしれません。もしくは、有効そうな変数だけを残して他はふるい落としておきたくなるかもしれません。k-最近傍法で説明したように正規化と言ってすべての変数を平均0、標準偏差1に変換することもよくあります。
しかし、これらの作業をする時にテストデータも含めてはいけません。なぜなら、現実に予測したい「新しい未知のデータ」に対してこれらの情報を得ることはありえないからです。テストデータは未知のデータの代わりに使うものなので、限りなく未知のデータと同じように扱わなければいけません。
モデルの評価のメトリック
ここまで精度精度と言ってきましたが、はたして精度とは何でしょうか?
単純のため、1(合格)か0(不合格)で分類する問題を考えましょう。
あなたはモデルを作り、そのモデルをもとにテストデータを予測しました。
すると、「予測が1か0か」掛ける「実際は1か0か」でテストデータの各点は4パターンのどれかに分類されます。
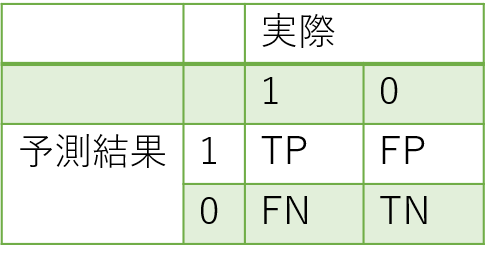
画像はhttps://www.minminblog.com/entry/recall_precisionから拝借しました。
ここで、実際に1(合格)でモデルでも1(合格)なのをTP (True Positive)、実際に1だがモデルでは0と予測されたのがFN (False Negative)、実際に0でモデルでも0と予測されるのがTN (True Negative)、実際に0だがモデルでは1と予測されるのがFP (False Positive)と呼びます。
分類問題における最も自然な定義は、正解率つまり
精度=\frac{TP+TN}{TP+TN+FN+FP}
です。これが一般的に__精度(accuracy)__と呼ばれるもので、確かにこれは汎用的に使えるメトリックです。
他のメトリックを紹介する前に、次のような問題を考えましょう。
あなたは健康診断のデータから、ある病気のスクリーニングをしようと思っています。
その病気は経験的に0.1%ほどの有病率であることがわかっています。
機械学習によってあなたは患者を発見することができるでしょうか。
この問題に対しては、今この場で精度99.9%のモデルを作ることができます。
どうすれば良いかというと、全員を「病気はない」と診断すればよいのです。そうすれば99.9%の健康な人が正しく診断され、このモデルの精度は99.9%です。
では、このモデルに意味があるでしょうか?もちろん何の役にもたちません。では、どのようにモデルを評価すべきでしょう?
自然な発想は、有病者の何%を発見できたか、です。これはリコール (Recall)もしくは感度 (Sensitivity)と呼ばれます。
感度=\frac{TP}{TP+FN}
しかし、このメトリックも簡単に改善できます。全員を有病者と診断すればよいのです。そうすれば感度は100%です。ではそのモデルに意味はあるでしょうか?同じく意味はありません。
では、有病者とモデルが判断した中での正解率はどうでしょう?これは適合率 (Precision)と呼ばれる指標で、
適合率=\frac{TP}{TP+FP}
と表されます。
しかしこれにも問題があります。ほとんどの被験者を健康と判断し、非常に病気の疑いが強い被験者だけを病気と判断するモデルを作れば適合率は非常に高くなりますが、ほとんどの有病者は見逃されます。
色々なメトリックを見てきましたが、どれもこの問題に適してはいませんでした。ではどうすればよいのでしょう?
正解は、これらのメトリックを総合的に判断するしかない、です。
Fスコア=感度×適合率、のような指標もありますが、これも万能とは言えません。
一般的に感度と適合率はトレードオフの関係にあります。これらのバランスが適切になるようなモデルを選択するのは、人間の仕事です。
モデルの選択 - クロスバリデーション
バリデーションデータ
複数のモデルから、実用に使うモデルを選び、その精度を評価することを考えましょう。
これは、ロジスティック回帰 vs k最近傍法かもしれませんし、k最近傍法のkを選ぶプロセスかもしれません。
このためにどのような手続きを踏めばよいでしょうか?
テストデータに対してそれぞれのモデルを当てはめて、テストデータで精度(単純のため、精度でモデルを選ぶとします)のもっとも高いモデルを選び、その精度がモデルの精度であると思えばよいのでしょうか?
残念ながら、問題はそれほど単純ではありません。こうして得られた精度は、正しい「未知のデータに対する精度」ではありません(__バイアスされている(biased)__といいます)。
これはなぜでしょうか。簡単な例を考えましょう。
あなたはできるだけ大きい目の出るサイコロが欲しいです。
2つのサイコロ(AとB)を10回ずつ投げて、出た目の平均値を比較します。Aの平均は3.2で、Bの平均は4.0でした。
あなたはBのサイコロを選んで、このサイコロは出る目の平均が4.0のサイコロであると言えるでしょうか
まず、Bの方がよいという推論はどうしようもありません。何度サイコロを振っても平均値の大きいサイコロ、小さいサイコロが出てしまうことは避けられません。なので、サイコロBを選ぶという選択は仕方ありません。実際、もしサイコロに性能差があれば、より性能の高いサイコロ(モデル)を選べる可能性の方が高いでしょう。
では、期待値はどうでしょう?もちろんこの例はサイコロなので、出る目の平均値は3.5であるはずです。なので、この4.0がサイコロBの出る目の期待値であると思ってはいけません。ではどのようにこのサイコロBの期待値を求めればよいのでしょう?
答えは「もうあと何回か振ってみる」です。
あと何回か振ってみれば、その平均値は理想的にはサイコロBの出る目の期待値(3.5)になります。
何が問題だったのでしょう?実は、「出た目の平均値が大きいサイコロを選ぶ」作業が問題でした。
ランダム性のあるものを複数並べて、最も大きいものを選ぶと、その値は真の期待値とは異なってしまいます。なぜならそれは「たまたま上手くいった」部分があるからです。
これを機械学習に置き換えると、複数のモデルをテストデータに適用し、最も精度の高いモデルを選んできた場合、その精度は過剰によく見積もられている可能性が高いです。
では、どのような手続きを取るのがよいでしょうか?実は、最初にデータを8:2でトレーニングとテストに分けたところでもう一工夫必要でした。
先に答えを示すと、以下のようなステップを取ることができます。
- データを7:1:2でトレーニング、バリデーション、テストデータに分ける
- トレーニングデータを使って複数のモデルを作る
- バリデーションデータに各モデルを当てはめて、最も精度の良いモデルを選ぶ
- 選んだタイプのモデルについて、トレーニングデータ+バリデーションデータでもう一度モデルを作る
- 4で作ったモデルをテストデータに当てはめて未知のデータに対する精度を評価する
こうすれば、バリデーションデータを使って、out-of-sampleでモデルを比較することができます。
その上、テストデータにはステップ5まで一度も触れていない(テストデータはモデルの作成にも選択にも使われていない)ため、テストデータを使った精度評価はフェアなものとなっています。このテストデータでの評価が、先ほどの例でいう、「サイコロを振りなおす」に対応しています。
クロスバリデーション
基本的には先ほどのプロセスで十分なのですが、これだと平均的にはよくないモデルが「たまたま」バリデーションデータセットでうまくいってしまうことがあります。
同じ実験を何回も繰り返すことができれば、結果が安定して(大数の法則)本当に良いモデルを見つけられることが期待されますが、残念ながらデータは限られています。
そこで登場するのが__クロスバリデーション__です。
- データを8:2でトレーニング、テストデータに分ける
- トレーニングデータを10等分して1-10の番号をつける
- 1-9番をトレーニング(仮)とし、10番をバリデーション(仮)とする
- トレーニングデータ(仮)を使って複数のモデルを作る
- バリデーションデータ(仮)に各モデルを当てはめて、精度を確認する
- バリデーション(仮)に使う番号を変えながら、2-5を繰り返し、最も平均精度が高いモデルを選ぶ
- 選んだタイプのモデルについて、トレーニングデータ全体でもう一度モデルを作る
- 7で作ったモデルをテストデータに当てはめて未知のデータに対する精度を評価する
というプロセスにのっとるのがクロスバリデーションです。
何をしているかというと、最初にデータをトレーニングとテストに分けた後、トレーニングデータの一部をバリデーションに使ってモデルの精度を評価することを繰り返します。そうして取った平均的な精度は、よりモデルの精度を正しく反映していると考えられます。
まとめ
今回はモデルをどのように評価し、選択すべきかについて書きました。
モデルの選択と評価は何も考えずにやると簡単に間違えてしまいます。
基本的には、「モデルの作成に使ったデータでモデルを評価してはいけない」という大原則を守るようにしてください。