なぜ三角形の内角の和が180度になるのか?
Web検索してもなかなかよい証明(説明)が見つからないので書いてみました。
錯角や同位角を使った証明も、錯角や同位角への疑問を生みスッキリしませんよね。
ヒントは外角の和にあります。
(追記)
ユークリッド幾何、すなわち小・中学生が習う図形の範囲を取り扱います。
証明ではありません。小学生でも直感的に理解できる説明を試みました。
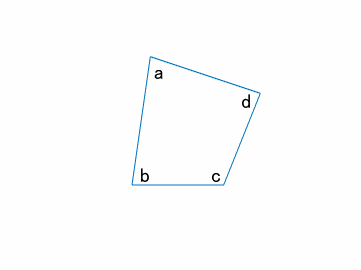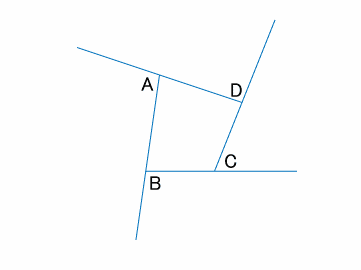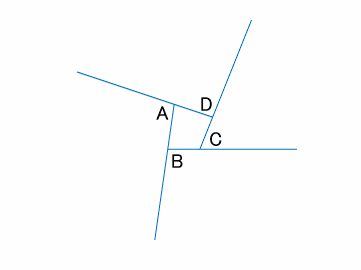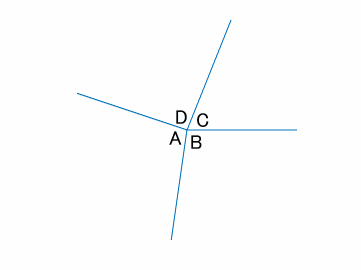
三角形
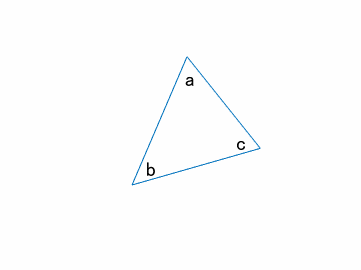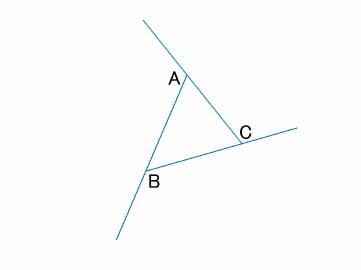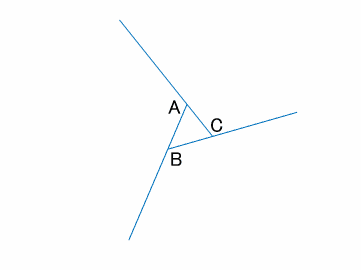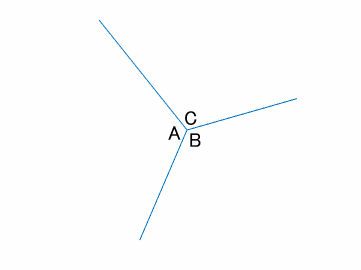
三角形の外角の和
ある三角形の内角をそれぞれ$a, b, c$とします。
それらの内角に対応する外角をそれぞれ$A, B, C$とします。
それぞれの内角と外角の和は$180^\circ$です。
a+A=180^\circ\\
b+B=180^\circ\\
c+C=180^\circ\\
この三角形を遠くから眺めてみましょう。(下図)
外角の和は$A+B+C=360^\circ$であることがわかります。
三角形の内角の和
次に、すべての内角と外角の和を求めてみます。
三角形は頂点が3つで、内角と外角の対は3つあります。
三角形のすべての内角と外角の和は
\begin{align}
a+A+b+B+c+C&=3\cdot180^\circ\\
(a+b+c)+(A+B+C)&=540^\circ\\
\end{align}
であり、外角の和は$A+B+C=360^\circ$なので、
\begin{align}
(a+b+c)+360^\circ&=540^\circ\\
a+b+c&=540^\circ-360^\circ=180^\circ
\end{align}
となり、三角形の内角の和は$180^\circ$であることがわかります。
四角形
四角形の外角の和
下図から三角形の場合と同様に、四角形の外角の和も$A+B+C+D=360^\circ$になります。
四角形の内角の和
四角形は頂点が4つで、内角と外角の対は4つあります。
すべての内角と外角の和は
\begin{align}
(a+b+c+d)+(A+B+C+D)&=4\cdot180^\circ=720^\circ
\end{align}
であり、外角の和は$A+B+C+D=360^\circ$なので、
\begin{align}
(a+b+c+d)+360^\circ&=720^\circ\\
a+b+c+d&=720^\circ-360^\circ=360^\circ
\end{align}
となり、四角形の内角の和は$360^\circ$になります。
n角形
n角形の外角の和
三角形や四角形と同様に考えると、n角形の外角の和も同じ$360^\circ$です。
n角形の内角の和
\begin{align}
内角の和&=n\cdot180^\circ-外角の和\\
&=n\cdot180^\circ-360^\circ\\
&=(n-2)\cdot180^\circ
\end{align}
となります。
凹多角形
少なくとも一つの内角の大きさが$180^\circ$を超えるような多角形を凹多角形と呼びます。
凹多角形の外角の和
凹多角形の場合は$180^\circ$を超える内角を持つ頂点での外角は負の値になります。それでも外角の和は凸多角形と同じく$360^\circ$になります。
凹多角形の内角の和
凹多角形の外角の和は凸多角形の外角の和と同じなので、凹多角形の内角の和も凸多角形の内角の和と同じになります。
星型多角形
上記は辺が交差しない多角形のお話でした。
星型のような多角形の場合はどうでしょうか?
星型多角形の外角の和
ここでは、すべての頂点を一筆書きで結んでできる下図のような星型五角形について考えます。
最初に辺EAを頂点Aに向かって出発したとします。頂点Aに達すると外角∠Aだけ進行方向を変えて頂点Bに向かいます。同様に各頂点B, C, D, Eで外角∠B, ∠C, ∠D, ∠Eだけ進行方向を変えて最初の辺EAに戻ります。この星型五角形を一周する間に進行方向は2回転しています。すなわち、この星型五角形の外角の和は$720^\circ$です。参考:GeoGebra:星型五角形の外角の和
なお、上記で述べたような辺が交差しない多角形でも同じように、外角の和を多角形を一周する間の進行方向の回転角と考えることができ、辺が交差しない多角形の外角の和は$360^\circ$(1回転)です。