目次
1.データの生成
2.ソフトマックス線形分類の学習
2.1.パラメータの初期化
2.2.クラススコアを算出
2.3.損失の計算
2.4.逆伝播による解析的勾配の計算
2.5.パラメータの更新を行う
2.6.すべてをまとめて:ソフトマックス分類器の学習
3.ニューラルネットワークの学習
4.概要
このセクションでは、2次元のトイ・ニューラル・ネットワークの完全な実装を説明します。まず、単純な線形分類器を実装し、次にそのコードを2層のニューラルネットワークに拡張します。見ての通り、この拡張は驚くほど簡単で、ほとんど変更の必要はありません。
1. データの生成
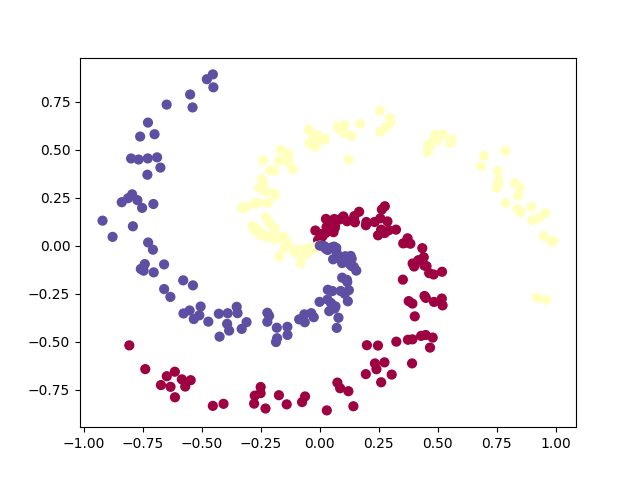
簡単には線形分離できない分類データセットを作ってみましょう。私たちがよく使う例はスパイラルデータセットで、次のようにして生成できます。
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0.0,1,N) # radius
t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()
おもちゃのスパイラルのデータは、3つのクラス(青、赤、黄)で構成されており、直線的に分離できません。
通常であれば、各特徴量の平均値がゼロ、標準偏差が1単位になるようにデータセットを前処理したいところですが、今回は特徴量がすでに-1から1の範囲に収まっているので、このステップは省略します。
2. ソフトマックス線形分類の学習
2.1. パラメータの初期化
まず、この分類データセットに対してソフトマックス分類器を学習させましょう。前のセクションで見たように、Softmax分類器は線形スコア関数を持ち、クロスエントロピー損失を使用します。線形分類器のパラメータは、各クラスの重み行列Wとバイアスベクトルbからなります。まず,これらのパラメータを乱数で初期化しましょう.
# パラメータをランダムに初期化
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
$ D = 2 $ が次元、$ K = 3 $がクラスの数であることを思い出してください。
2.2. クラススコアの算出
これは線形分類器なので,1回の行列乗算ですべてのクラススコアを非常に簡単に並列に計算することができます.
# 線形分類器のクラススコアの算出
scores = np.dot(X, W) + b
この例では、300個の2次元ポイントがあるので、この乗算の後、配列のスコアはサイズ[300 × 3]となり、各行には3つのクラス(青、赤、黄)に対応するクラススコアが表示されます。
2.3. 損失の計算
損失関数とは,計算されたクラススコアに対する不満を定量化する微分可能な目的語です.直感的には,正しいクラスが他のクラスよりも高いスコアを持つようにしたいと思います.そうであれば,損失は小さく,そうでなければ,損失は大きくなります.この直感を定量化する方法はたくさんありますが、この例ではSoftmax分類器に関連するクロスエントロピー損失を使用します。思い出してください。$ f $が1つの例に対するクラススコアの配列(例えばここでは3つの数字の配列)である場合、Softmax分類器はその例に対する損失を次のように計算します。
L_i = -log(\frac{e^{fyi}}{\Sigma_j e^{fj}})
ソフトマックス分類器は、$ f $の各要素を、3つのクラスの(正規化されていない)対数確率を保持していると解釈していることがわかります。正規化されていない)確率を得るためにこれらを指数化し、確率を得るためにそれらを正規化します。したがって,logの中の式は,正しいクラスの正規化された確率である.この式がどのように機能するかに注意してください。この量は常に0と1の間にあります。正しいクラスの確率が非常に小さい(0に近い)場合、損失は(正の)無限大に向かっていきます。逆に、正しいクラスの確率が1に近づくと、$ log(1)=0 $なので、損失は0になります。 したがって、$ Li $の式は、正しいクラスの確率が高いときは低く、低いときは非常に高くなります。
また、Softmax分類器の完全な損失は、学習例と正則化の平均クロスエントロピー損失として定義されることを思い出してください。
L = \frac{1}{N} \sum_{i} L_i + \frac{1}{2} \lambda \sum_{k} \sum_{l} w_{k,l}^2
上記で計算したスコアの配列があれば、損失を計算することができます。まず、確率の求め方は簡単です。
num_examples = X.shape[0]
# 正規化されていない確率の取得
exp_scores = np.exp(scores)
# 各例ごとに正規化する
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
サイズ [300 x 3] の配列 $ probs $ ができ、各行にクラスの確率が入ります。特に、正規化したので、すべての行の合計が1になりました。これで、各例で正しいクラスに割り当てられた対数確率を問い合わせることができます。
correct_logprobs = -np.log(probs[range(num_examples),y])
配列 $ correct_logprobs $は,各例の正しいクラスに割り当てられた確率を表す 1 次元の配列です.完全な損失は、これらのログ確率と正則化損失の平均です。
# 損失の計算:平均クロスエントロピー損失と正則化
data_loss = np.sum(correct_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss
このコードでは、正則化の強さλは$ reg $の内部に格納されています。正則化に$ 0.5 $を乗じた便利な要素は、すぐに明らかになるでしょう。これを最初に(ランダムなパラメータで)評価すると、$ loss = 1.1 $となり、$ -np.log(1.0/3) $となります。これは、初期のランダムな重みが小さい場合、すべてのクラスに割り当てられる確率が約3分の1になるからです。そこで、損失をできるだけ小さくしたいと考え、絶対的な下限として$ loss=0 $を設定しました。しかし、損失が小さければ小さいほど、すべての例で正しいクラスに割り当てられる確率が高くなります。
2.4. 逆伝播による解析的勾配の計算
損失を評価する方法ができたので、今度はそれを最小化する必要があります。これには勾配降下法を使います。つまり,(上の図のように)ランダムなパラメータから始めて,パラメータに対する損失関数の勾配を評価し,損失を減らすためにどのようにパラメータを変更すべきかを知るのです.中間変数pを導入しましょう。これは(正規化された)確率のベクトルです。ある例の損失は
p_k = \frac{e^{fk}}{\Sigma_j e^{fj}}\;\;\;\;\;\;\;\;\;\;L_i=-log(p_{yi})
次に、この例が完全な目的に寄与する損失$ L_i $を減らすために、$ f $の内部で計算されたスコアがどのように変化すべきかを理解したいと思います。つまり、勾配$ \frac{∂L_i}{∂f_k} $を導き出したいのです。損失$ L_i $は$ p $から計算されますが、これはfに依存します。鎖の法則を使って勾配を導出するのは、読者にとっては楽しい作業ですが、いろいろなことが相殺された後、最終的には極めてシンプルな解釈ができることがわかります。
\frac{∂L_i}{∂f_k}=p_k-1(y_i=k)
この表現がいかにエレガントでシンプルであるかに注目してください。計算した確率が$ p = [0.2, 0.3, 0.5] $で、正しいクラスは真ん中のクラス(確率$ 0.3 $)だったとします。この導出によると、スコアの勾配は$ df = [0.2, -0.7, 0.5] $となります。勾配の解釈を思い出してみると、この結果は非常に直感的であることがわかります。スコアベクトルfの最初または最後の要素(不正解のクラスのスコア)を増加させると、(正の符号+0.2と+0.5により)損失が増加し、予想通り損失の増加は悪いことです。しかし、正しいクラスのスコアを増やすことは、損失にマイナスの影響を与えます。勾配が$ -0.7 $なのは、正しいクラスのスコアを増やすと、損失の$ L_i $が減ることを示しており、理にかなっていると思います。
これらはすべて,以下のコードに集約されます.probsは,各例のすべてのクラスの確率を(行として)格納していることを思い出してください.dscoresと呼ばれるスコアの勾配を得るためには,以下のようにします。
dscores = probs
dscores[range(num_examples, y] -= 1
dscores /= num_examples
最後に、$ scores = np.dot(X, W) + b $という結果が出たので、($ dscores $に格納されている)$ scores $の勾配を利用して、$ W $と$ b $に逆伝播することができます。
d_W = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
d_W += reg*W # 正則化の勾配を忘れずに
ここでは、行列の乗算処理を逆伝播して、正則化による寄与を加えていることがわかります。なお、正則化勾配は、その損失寄与度に定数$ 0.5 $を用いたため、非常にシンプルな形の$ regW $となっています(つまり、$ \frac{d}{dw}(\frac{1}{2}λw^2)=λw) $。これは、勾配の表現を単純化するための一般的な便宜上のトリックです。
2.5. パラメータの更新を行う
勾配を評価したことで、すべてのパラメータが損失関数にどのように影響するかがわかりました。ここでは、損失を減らすために、負の勾配方向にパラメータの更新を行います。
#パラメータの更新を行う
W += -step_size * dW
b += -step_size * db
2.6. すべてをまとめて:ソフトマックス分類器の学習
これらをまとめると、勾配降下法を用いてソフトマックス分類器を学習するための完全なコードは以下の通りです。
#Train a Linear Classifier
# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength
# gradient descent loop
num_examples = X.shape[0]
for i in range(200):
# evaluate class scores, [N x K]
scores = np.dot(X, W) + b
# compute the class probabilities
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
# compute the loss: average cross-entropy loss and regularization
correct_logprobs = -np.log(probs[range(num_examples),y])
data_loss = np.sum(correct_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss
if i % 10 == 0:
print "iteration %d: loss %f" % (i, loss)
# compute the gradient on scores
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
# backpropate the gradient to the parameters (W,b)
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # regularization gradient
# perform a parameter update
W += -step_size * dW
b += -step_size * db
これを実行すると、出力が表示されます。
iteration 0: loss 1.096956
iteration 10: loss 0.917265
iteration 20: loss 0.851503
iteration 30: loss 0.822336
iteration 40: loss 0.807586
iteration 50: loss 0.799448
iteration 60: loss 0.794681
iteration 70: loss 0.791764
iteration 80: loss 0.789920
iteration 90: loss 0.788726
iteration 100: loss 0.787938
iteration 110: loss 0.787409
iteration 120: loss 0.787049
iteration 130: loss 0.786803
iteration 140: loss 0.786633
iteration 150: loss 0.786514
iteration 160: loss 0.786431
iteration 170: loss 0.786373
iteration 180: loss 0.786331
iteration 190: loss 0.786302
約190回の繰り返しの後、何かに収束したことがわかります。トレーニングセットの精度を評価することができます。
# トレーニングセットの精度評価
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))
これで49%と表示されました。決して良いとは言えませんが、データセットが線形分離できないように構築されていることを考えると、驚くことではありません。また、学習した判定境界をプロットすることもできます。