いよいよ連載も終盤に近づいてきました。
今日はレーダ技術者の腕の見せ所である方位推定です。
前回まではFFTくらいのレベルの数学で事足りましたが、方位推定では正則行列や固有値、固有ベクトルなどの線形代数学が必要になります。(今の高校生って行列やらないんですよね。。。かなC)
こちらが今日のトピックスです。
- 処理の基礎
- 古(いにしえ)の手法
- Beamformer Method
- Capon Method
- LP法
- 古の手法比較
古の手法以降は次回にしないと頭がパンクするので、今回は古典的なものを紹介して終わります。
処理の基礎
初回の内容を思い出してください。アレーアンテナは各アンテナの受信に重みをつけて出力を合成するんでしたね。
例えば、角$\theta$から電波が来た場合、各アンテナへのは以下に示すように、位相差がついて受信されます。

各アンテナの受信信号は後段でヒルベルト変換され、複素数信号
$$x_k(t)=x_{rk}+jx_{ik}$$
になります。(90deg遅れの信号を合成します。)重みも複素数ですからこうなります。
$$w_k=w_{rk}+jw_{ik}$$
出力信号$y_k(t)$はこうです。
$$y_k(t)=w_k^*x_k(t)$$
共役複素数をとるのは、$w, x$の虚部同士の掛け算で符号がひっくり返らないようにするためです。
各アンテナの入力、重み、出力をベクトル化するとこうなります。
\boldsymbol{X}(t)=[x_1(t),\cdots , x_K(t)]^T\\
\boldsymbol{W}=[w_1,\cdots , w_K]^T\\
y(t)=\boldsymbol{W}^H\boldsymbol{X}(t)=\boldsymbol{X}^H(t)\boldsymbol{W}
しかし、$y(t)$のまま処理すると時間変化の影響をモロに喰らうので、時間平均をとって平均電力を計算します。
P=\cfrac{1}{2}E[|y(t)|^2]=\cfrac{1}{2}\boldsymbol{W}^HE[\boldsymbol{X}(t)\boldsymbol{X}^H(t)]\boldsymbol{W}=\cfrac{1}{2}\boldsymbol{W}^HR_{xx}\boldsymbol{W}
実部の電力を計算するので係数の$1/2$がついてます。$E[\cdot]$はアダマール積の時間平均です。$E[\boldsymbol{X}(t)\boldsymbol{X}(t)^H]$は相関行列と呼ばれ$Rxx$で表します。
R_{xx}=E[\boldsymbol{X(t)X^H(t)}]\\
=\begin{bmatrix}
E(x_1(y) \cdot x_1(t)^*) & E(x_1(y) \cdot x_2(t)^*) & \cdots & E(x_1(y) \cdot x_K(t)^*) \\
E(x_2(y) \cdot x_1(t)^*) & E(x_2(y) \cdot x_2(t)^*) & \cdots & E(x_2(y) \cdot x_K(t)^*) \\
\vdots & \ddots & \ddots & \vdots \\
E(x_K(y) \cdot x_1(t)^*) & E(x_K(y) \cdot x_2(t)^*) & \cdots & E(x_K(y) \cdot x_K(t)^*)
\end{bmatrix}
前回までの距離・速度推定とは違って、受信信号間の位相差が読めればそれでいいので、方位推定だけなら変調は必要としません。
さあここまで理解できたら方位推定の準備は完了です(3割くらい)。
古のMethod
Beamformer Method
もっとも古典かつ、よく聞くレーダの方位推定がBeamformerです。
上の図より、$k$番目のアンテナの座標が$d_k$だった時、基準のアンテナとの位相差はこのようになります。
$$\psi_k=\cfrac{2\pi d_k}{\lambda}\sin(\theta)$$
基準アンテナとの経路差が$d_k\sin(\theta)$なので、それを位相差に変換したものですね。
一方、受信された波はヒルベルト変換で複素数に変換されています。それぞれのアンテナが$\psi_k$の位相差を持った状態ですね。そうすると、単純に重みは
$$w_k=e^{-j\psi_k}$$
とすれば、各アンテナの位相回転をキャンセルでき、同相合成できますよね??
$$\boldsymbol{W}=[w_1, w_2, \cdots, w_K]^T=\boldsymbol{a}(\theta)$$
$\boldsymbol{a}(\theta)$ですが、$\boldsymbol{W}$はあくまで「重み」であり、他の手法では違う値を使用します。しかしながらこのベクトルは波の位相差を示すベクトル、「モードベクトル」として使用するので、$\boldsymbol{a}(\theta)$とおきます。
Beamformer法は重みに含まれる角度$\theta$を$-90$〜$90$deg.までスウィープし、各方位の電力を重みによって同相合成しながら、出力電力のピークとなる角度を探す方法です。この方法ではピークがそのまま受信電力の大きさを表しています。この方法では$W$と$a(\theta)$は同じなので、正規化して
P=\cfrac{\boldsymbol{a}^H(\theta)\boldsymbol{R_{xx}a}(\theta)}{\boldsymbol{a}(\theta)^H\boldsymbol{a}(\theta)}
が角度スペクトラムです。
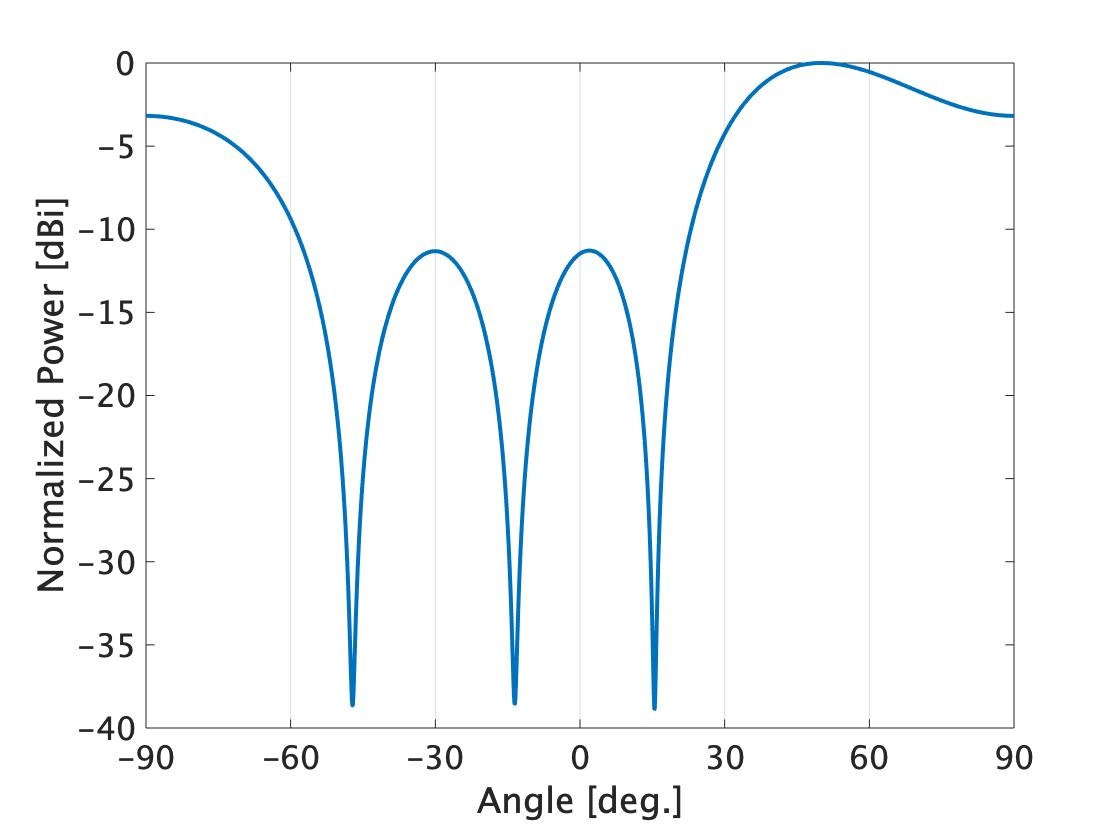
試しに、角度50deg.から波が到来したとして、Beamformerを適応してみます。
受信アンテナ数は4つでやってます。50degでピークがありますが、弱いですね。
Beamformerはアンテナの数が多いほど精度が良くなる(アンテナが多いほどビームが狭くなるので当然の結果ですが)ので、小型化には向かないものの、受信電力をそのまま出力する点ではメリットがあります。ただし、何も考えずに脳死でビームを振っているだけなところがデメリットです。ある方位の入射を同相で合成するのですが、原理上アレーアンテナはそれ以外の方向も拾ってしまいます。そのため、意図せず所望しない波を受信してSNが悪化する可能性があります。全く電波が来ていない方向をみている時に、他の方角からきた電波を受信しまうのは良いことではありません。また、Beamformerは、近いターゲットを分離する能力が低いので、複数ターゲットの推定には向いていません。
Capon Method
Capon法はBeamformerの
意図せず所望しない波を受信してSNが悪化する可能性がある
と言う部分を解決する方法です。イメージで言うと、ある方向をスキャンしてるとき、他の方角からきた電力の大きい電波を受信しないようにすると言うことです。Beamformerのスペクトルを見ると、15、-15、-50degあたりに電力の著しく低い点があります。電波屋さんの中ではこれを「ヌル点」と言うのですが、Caponは余分な方角の大きい電力にヌルを向けることで、所望波以外の寄与を最小にしようと言うものです。
条件を数式に落とすと、
\underset{\boldsymbol{W}}{min}\left(P=\cfrac{1}{2}\boldsymbol{W}^HR_{xx}\boldsymbol{W}\right)\\
subject\ to\ \boldsymbol{W}^H\boldsymbol{a}(\theta)=1
となります。これを満たす$\boldsymbol{W}$を求めれば良いのですが、めっちゃむずくてここに書ききれるボリュームじゃないので割愛。解はこうなります。
$$\boldsymbol{W_{capon}}=\cfrac{R_{xx}^{-1}\boldsymbol{a}(\theta)}{\boldsymbol{a}^H(\theta)R_{xx}^{-1}\boldsymbol{a}(\theta)}$$
よってスペクトルは、
$$P=\cfrac{1}{2}\boldsymbol{W_{capon}}^HR_{xx}\boldsymbol{W_{capon}}=\cfrac{1}{2\boldsymbol{a}^H(\theta)R_{xx}^{-1}\boldsymbol{a}(\theta)}$$
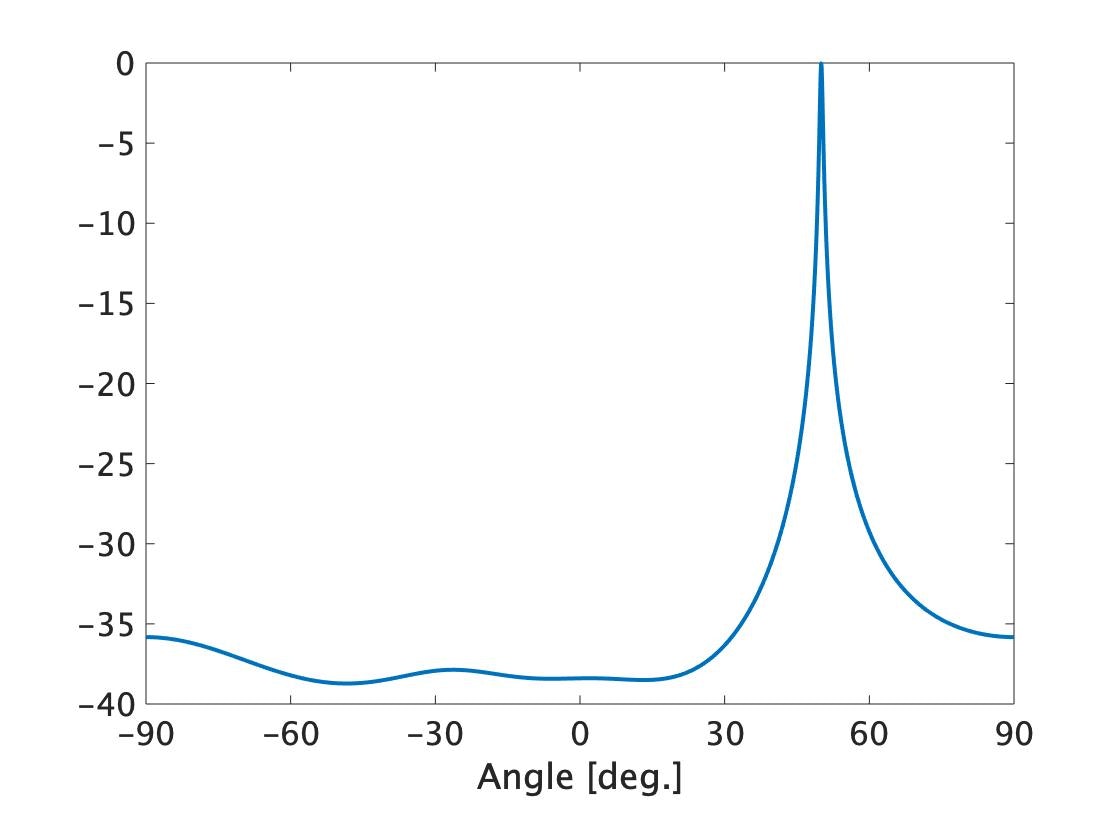
となります。これも50degから電波を入れてみましょう。
Beamformerよりもだいぶ鋭いピークがでますね。Caponは、観測方向以外の電力を最小化し、観測方向の電力はそのまま出力するので、ピークの高さは到来電力と等しくなります。電波が来ていない時は勝手にピークが消えるので便利です。
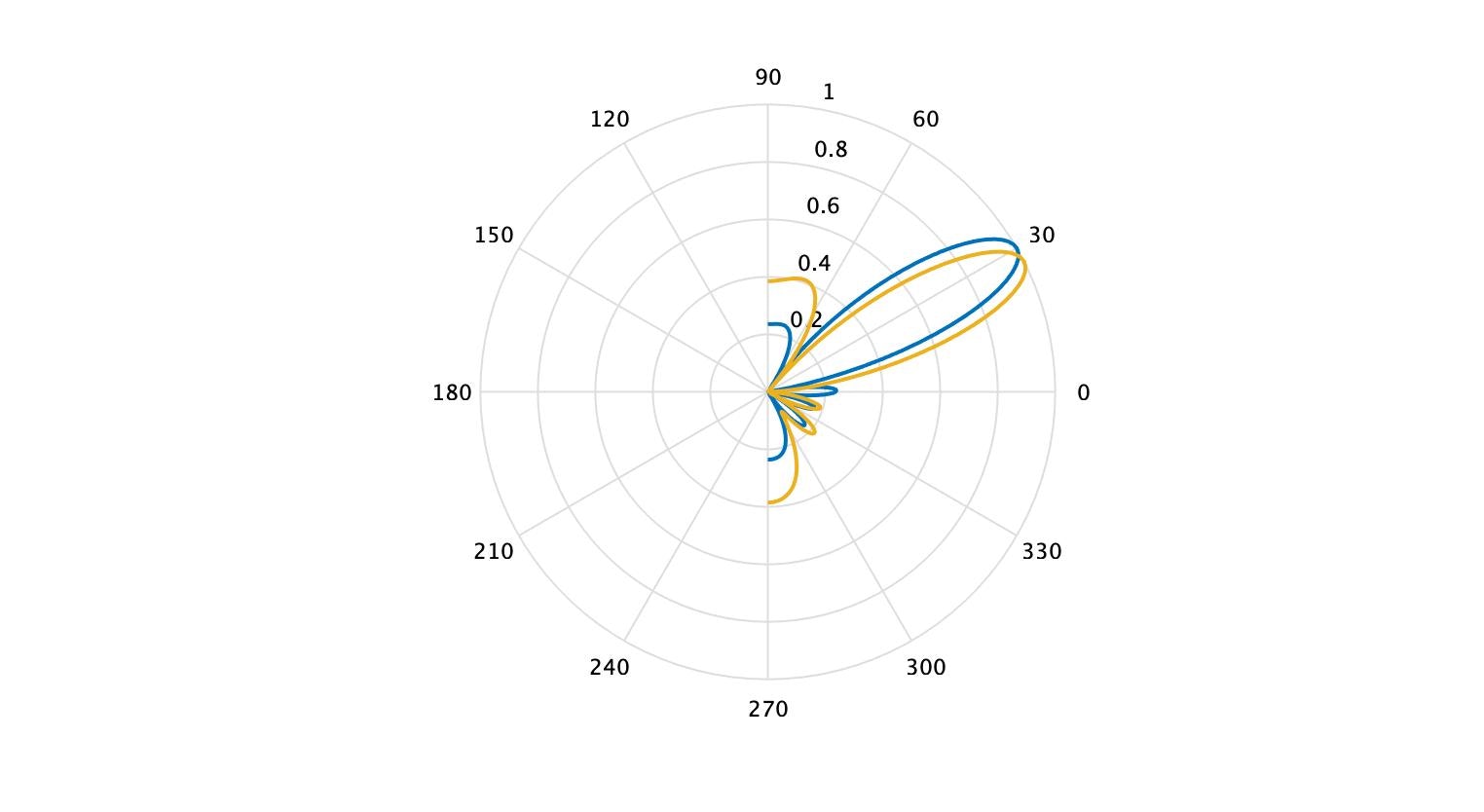
実際にCaponが所望波以外の到来波にビームを向ける様子がこれです。
0degと50degの方角から到来波が来ている状況で、30deg方向をスキャンしている様子です。青がBeamformer、黄色がCaponです。Caponは0、50deg方向にヌルを向けて、電力を最小化しています。一方Beamformerは30deg方向をスキャン中でも0、50deg方向の電波を拾ってしまっています。これが2手法のダイナミックレンジの差につながっています。
LP法
BeamformerとCaponは到来波の電力を最大化すると言う理念で作られていますが、逆の発想を持つ手法もあります。その一つがLP法です。LP法はLinear Predictionの略で、線形予測法と訳します。なんでこんな発想ができたかと言うと、Beamformerのスペクトルを見るとわかります。グラフ上のピークを読めと言われるより、ヌルを読めと言われたほうが正確に値が取れるじゃないですか。LPはスキャンしている角度の電力を最小化するように動き、電力が落ちる方向を推定する手法です。LP法は1素子目のアンテナの受信信号を他のアンテナの線形結合によって予測します。
$$x_1^p(t)=\sum^K_2w_k^*x_k(t)$$
実際の$x_1(t)$との誤差はこのようになります。
$$e(t)=x_1(t)-x_1^p(t)=\sum^K_1w_k^*x_k(t)=\boldsymbol{W}^H\boldsymbol{X}(t) \ \ \ (w_1=1)$$
この予測誤差を最小化することで重みを求めます。
$$E[|e(t)|^2]=2P$$
この問題は$w_1=1$の条件下で出力を最小化することになります。
\underset{\boldsymbol{W}}{min}\left(P=\cfrac{1}{2}\boldsymbol{W}^HR_{xx}\boldsymbol{W}\right)\\
subject\ to\ \boldsymbol{T}^T\boldsymbol{W}^*=1\\
\boldsymbol{T}=[1,0,\cdots,0]^T
$\boldsymbol{T}$の要素数は$K$です。Caponと同じく、これを解いて最適ウェイトを決めるとこうなります。
$$\boldsymbol{W_{LP}}=\cfrac{R_{xx}^{-1}\boldsymbol{T}}{\boldsymbol{T}^HR_{xx}^{-1}\boldsymbol{T}}$$
で、出力スペクトルをさっきと同じように計算すると所望方位がヌルになってしまうので、LPのときは逆数をとって
$$P=\cfrac{1}{|\boldsymbol{W_{LP}}^H\boldsymbol{a}(\theta)|^2}$$
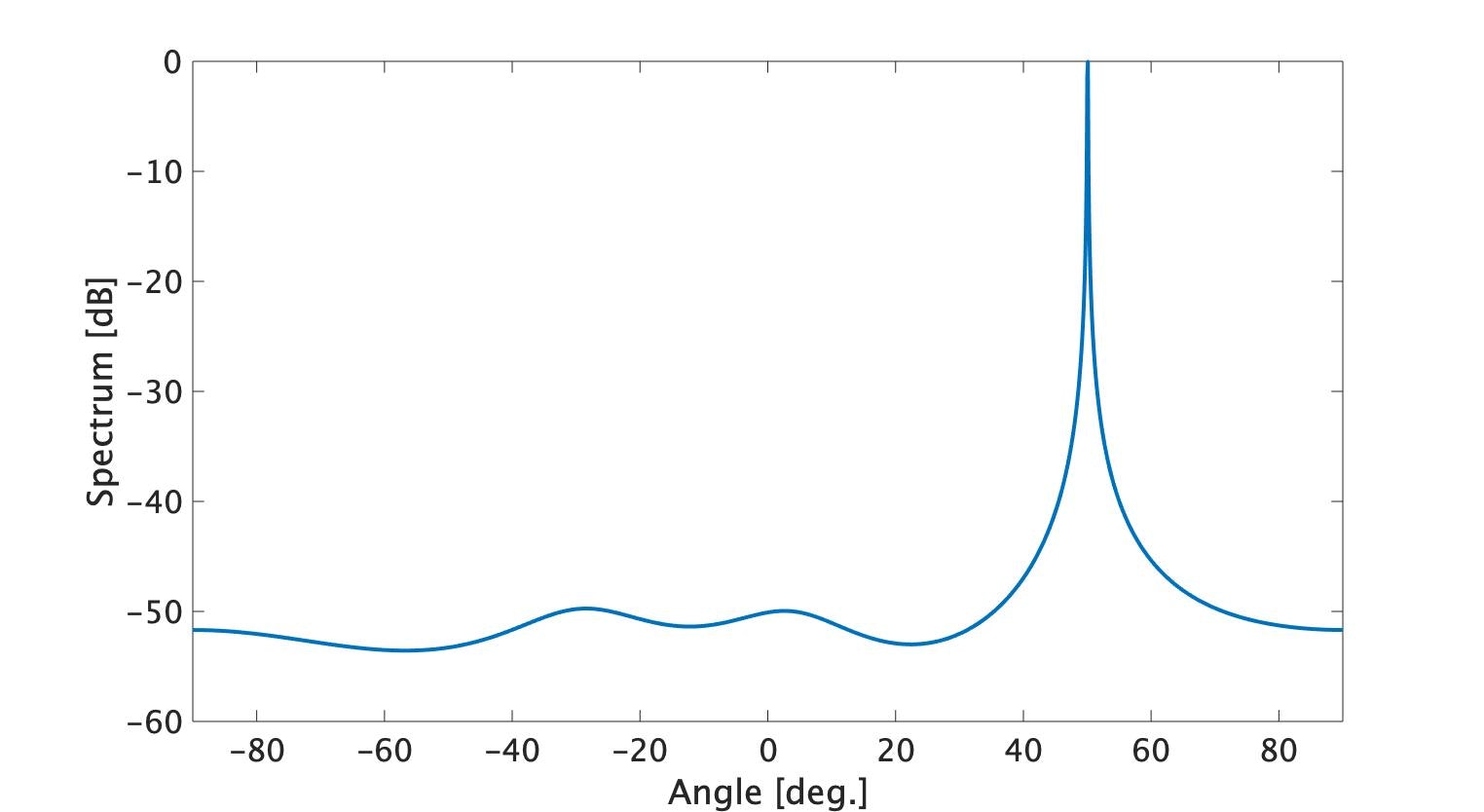
になります。LPも50deg方向にターゲットを置いてみましょう。
Caponと見た目が変わらないですが、ダイナミックレンジが大きいですね。
古の手法の比較
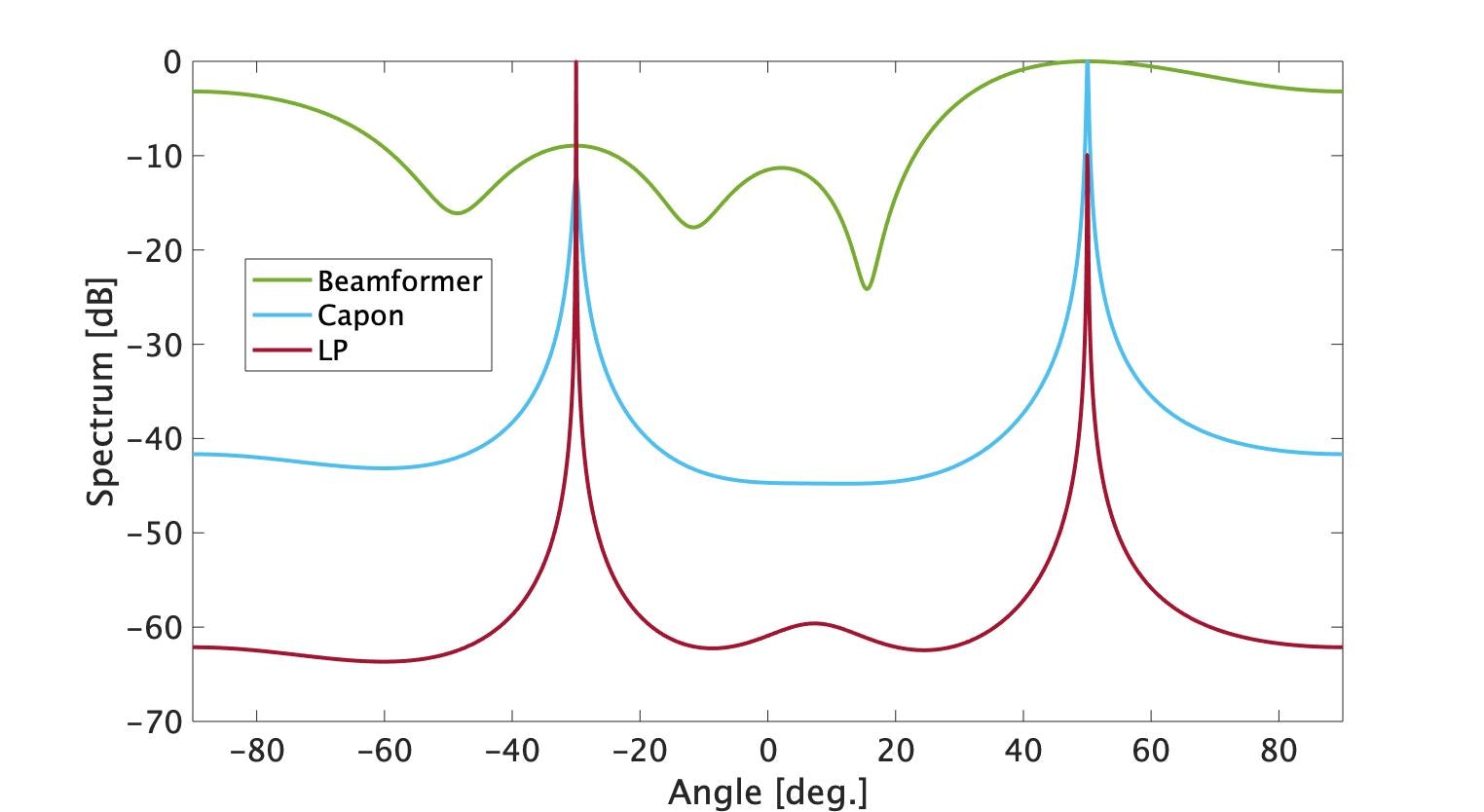
ここまでの手法で角度分離精度を比較しましょう。まず到来波の波源を(50m, 50deg)と(100m, -30deg)にしてみます。
さすがLPですねー。Beamformerは2ピークあるとは言い切れません。(色々やって分かったのですが、2つの波源の距離が等しいとCaponがうんちになります。その点Beamformerは優れてると言えるかも。)
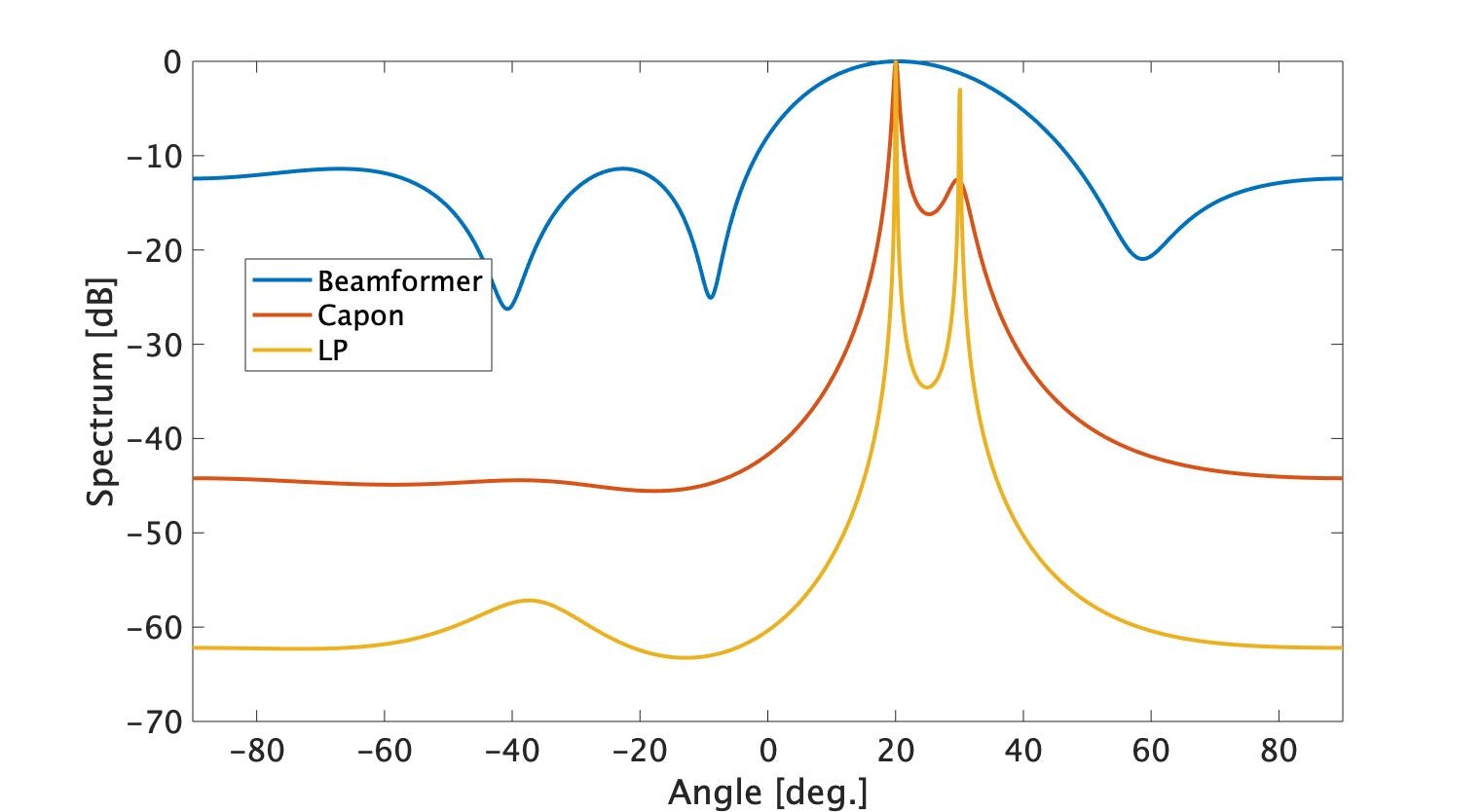
次はこの波源の方位を近くして、(50m, 20deg)と(100m, 30deg)にします。
もうBeamformerはだめですね。Caponはまだ2波の分離ができそうです。ここまでの手法で特徴をまとめるとこんな感じ。
| 理念 | 出力と受信電力の相関 | 計算量 | 分離能 | |
|---|---|---|---|---|
| Beamformer | 電力最大化 | 大 | 小 | 小 |
| Capon | 電力最大化 | 中 | 中 | 中 |
| LP | ヌル制御 | なし | 大 | 大 |
LPのだめなところはスペクトルの大きさと受信電力に相関がないことです。ノイズに対して大きいピークを向けることがあります。Caponが最も中庸な感じですが、中庸すぎて実際使ってないことが多いのでは?学会なんかの比較対象としてしかみないような。。。
3つの手法に共通して言えることは、「アンプの内部雑音が大きいと精度が落ちる」と言うことです。読んでわかると思いますがその辺の対策ヌルですよね。(次回への伏線)
まとめ
今回は太古の昔からある方位推定の手法を解説しました。いいところもあれば悪いところもあるって感じですね。Caponはなかなかいいんですが、平凡すぎて使えない。なんだか人間社会の縮図のようです。
次回はもっと近代的な手法を2つ紹介します。今回が多分一番ヘヴィーなので、じっくり色々調べながらでないと難しかったかもしれませんね。ではまた。