普通の代表値
専門家以外の人が把握している統計学っておそらく平均値が基準になっていて、そこから分散などを計算し、やりたいことの手掛かりにすると思います。
最近仕事で、**「どういう分布かわからない時にはどう見ればいいんだろう」**と疑問に思うことがありました。例えば実験データを見る時など、通常は正規分布や二項分布などの平均が最頻である物を想定すると思います。その前提がなかったら?どうやってデータの傾向を把握すればいいのでしょう。
そういうったことに詳しい方コメントくれたら嬉しいですが、自分なりに少し考えてみました。
平均値が実態をよく表さない時
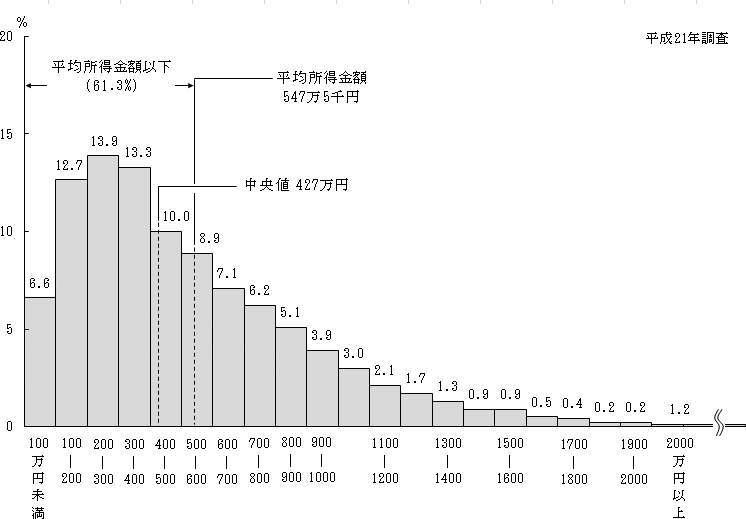
年収の話をする時などはしばしば平均年収を語られることが多く、**「俺そんなに貰ってねぇよ」**と文句を垂れる人が多いと思います。実際の日本の年収分布ってこうなっているそうです。
年収でなくても何かの統計データがこんな分布をしていたら、平均にあまり意味を感じませんよね。どうみても最頻値かせめて中央値がデータの実態をよく表すと思います。データの値を$x$、平均を$\bar{x}$として、分散は通常以下のように定義されます。
$$\sigma^2=\frac{1}{N}\sum_{n=1}^{N}(x_n-\bar{x})^2$$
これって平均からの差をばらつきとして定めてるじゃないですか。上のようなデータに対して使おうと思ったら明らかに不適切ですよね??
最頻値を基準にしてみる
じゃあ最頻値を基準にしてみるか。と思い分散を改造してみました。
$$\sigma'^2=\frac{1}{N}\sum_{n=1}^{N}(x_n-x_m)^2$$
$x_m$が最頻値です。そこそこいい指標にはなりそうですがいまいちピンとこないですね。データの裾野が広く分布してればいいですが、年収のように片側がギュッと詰まっている場合、ピーク位置が左に行くほど分散が小さくなってしまいそうです。
データ軸を修正する
もう一つ思いつく(というより頭の片隅にあった)方法としてx軸を対数軸などにしてグラフの形を変えちゃう方法です。
ただこれも裾野のデータがたくさんある時しか有効じゃないですよね。下限があるときついです。。。
なんかアイデアあったらください
僕はこの辺の知識が基礎レベル以下なのでこんなデータ解析の方法があるとかコメントでいただけるとありがたいです。分布が不確定なものをどう評価するか、これから少しずつ調べて行こうと思います。