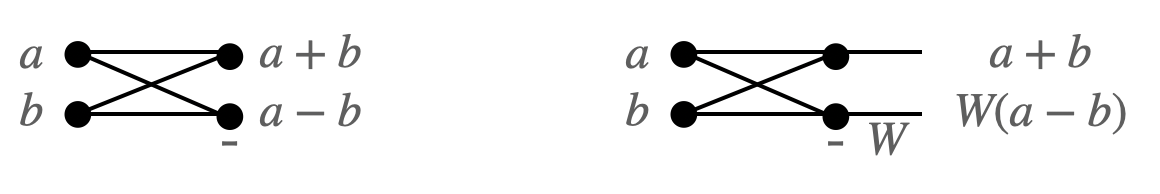今年もやってきました @motorcontrolman さん主催のアドベントカレンダー。
昨年に引き続き参加します。
僕はMATLAB原理主義者です。
今回はあらゆる分野で幅を利かせているFFTをとりあげようと思います。ネットを探せばいろんな解説がありますが、初学者に対する優しさがないものばかりであり、加えて**「理系、特に工学系の専攻だったならFFTのことなんて理解してるでしょ?」**みたいな風潮があり、うかつに質問できないことありますよね。
大丈夫です。多分大抵の人は概要すら理解していません。
この記事がみなさんの役に立てると嬉しいです。
そもそもフーリエ変換とは
まず原点に立ち返ってフーリエ変換とはなんなのでしょうか。みなさんご存知だと思いますが、任意の波形は三角関数の足しあわせに変換できるというもので、変数tを持つ任意の関数は
x(t) = a_0+a_{1}\sin\left(\frac{2\pi t}{T}\right)+b_{1}\cos\left(\frac{2\pi t}{T}\right)+\cdots+a_{n}\sin\left(\frac{2n\pi t}{T}\right)+b_{n}\cos\left(\frac{2n\pi t}{T}\right)+\cdots
とできます。sinとcosがいるのは、位相ズレを再現するためで、以下のように考えてもらってもいいです。
x(t) = c_0+c_{1}\sin\left(\frac{j2\pi t}{T}+\phi_1\right)+\cdots+c_{n}\sin\left(\frac{j2n\pi t}{T}+\phi_n\right)+\cdots
理解する上ではsin,cos両方ある式の方がいいかもしれません。
関数の直交
フーリエ変換の式(上式)の重要なところは各項が直交していて、冗長性が最小だということです。
ベクトルの基底はみなさんご存知だと思います。任意のベクトルはその次元の基底ベクトルの足し合わせによって一意に決まりますよね。
\boldsymbol{v} = a_0\boldsymbol{u_0}+a_1\boldsymbol{u_1}+\cdots+a_n\boldsymbol{u_n}+\cdots
$\boldsymbol{u_n}$成分を表現するためには$a_n$に値を入れるしかないのです。それがあるからベクトルの成分分解ができます。そして、このベクトルの表現が一意であるためには、他の基底ベクトル同士の足し合わせによって別の基底ベクトルが表現できてはいけません。これは各基底ベクトルの内積がゼロであることと同義です。これが直交です。ベクトルでいう直交は、本当にベクトル同士の間の角が直角ということです。(3次元以上のときに直角とは??となりますが許して)
例えばn本の基底ベクトルを選んできて他の基底ベクトルを表現しようとしても、n本全てのベクトルが目的の基底ベクトルと直角なわけですから、表現のしようがありません。**「ある成分を表現するには、その項の係数を使うしかない」**これが直交の重要ポイントです。
フーリエの式はベクトルではありませんが、ベクトルの足し合わせ的な形式をしています。いろんな周期の正弦波の足し合わせですよね。ベクトルと同じように扱うため、区間Tにおいて関数$f, g$の直交をこのように定義します。
\int_{-T/2}^{T/2} fg^*=0
アスタリスクは複素共役です。区間Tで関数の積を積分してゼロであれば、その関数同士は直交です。関数の時は瞬時値で直交を言いにくいので積分を取ります。そして積を取っているのはベクトルの内積と同じ意味です。内積がゼロなら直交ということと同じことです。
フーリエ変換の直交性
x(t) = a_0+a_{1}\sin\left(\frac{2\pi t}{T}\right)+b_{1}\cos\left(\frac{2\pi t}{T}\right)+\cdots+a_{n}\sin\left(\frac{2n\pi t}{T}\right)+b_{n}\cos\left(\frac{2n\pi t}{T}\right)+\cdots
この式の各項は直交していますね。実数なので複素共役は考えなくていいです。一通り積分するとわかると思います。
\int_{-T/2}^{T/2}\sin(2\pi nt/T)dt = 0\\
\int_{-T/2}^{T/2}\cos(2\pi nt/T)dt = 0\\
\int_{-T/2}^{T/2}\sin(2\pi nt/T)\sin(2\pi mt/T)dt = 0\\
\int_{-T/2}^{T/2}\cos(2\pi nt/T)\cos(2\pi mt/T)dt = 0\\
\int_{-T/2}^{T/2}\sin(2\pi nt/T)\cos(2\pi mt/T)dt = 0\\
\int_{-T/2}^{T/2}\cos(2\pi nt/T)\sin(2\pi mt/T)dt = 0
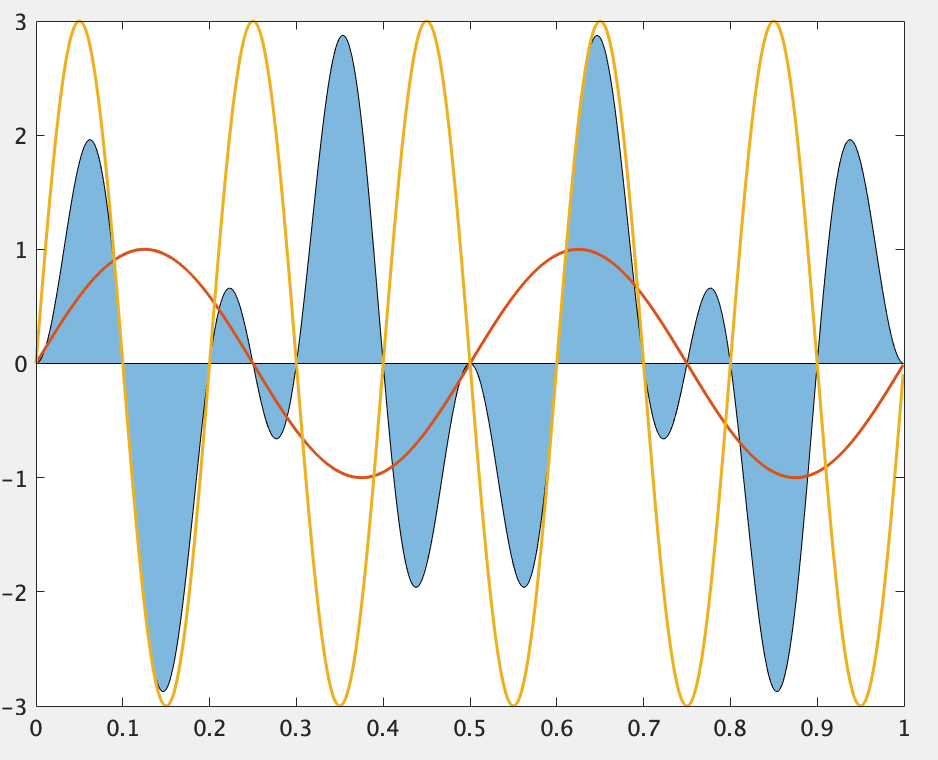
最初の2つは言わずもがなですね。残りは積和変換してもらえばいいと思いますが、以下のグラフ(2つの正弦波とその積の面積)の通り、プラスマイナスで対称になっているエリアができて積分がゼロになります。
このようにsin○の項、cos○の項は直交していて、$sin(2\pi nt/T)$の成分の大きさは$a_n$によってしか表現できないということになります。逆のことを言うと、関数x(t)を正弦波の周期ごとに分けることができれば、振幅によってその成分の大きさが把握できると言うことです。
複素フーリエ変換
FFTは基本的に複素フーリエです。なので上の話を複素数に拡張します。複素数の場合は正弦波の他しあわせではなく、複素平面上の角速度の異なる等速円運動の足し合わせとなります。回転の足し合わせなので、プラス方向の回転とマイナス方向の回転があります。直交性はもういちいちやりませんが、興味のある方はやってみてください。
x(t) = \cdots +c_{-n}\exp\left(\frac{-j2n\pi t}{T}\right)+\cdots+c_{-1}\exp\left(\frac{-j2\pi t}{T}\right)+c_0+c_{1}\exp\left(\frac{j2\pi t}{T}\right)+\cdots+c_{n}\exp\left(\frac{j2n\pi t}{T}\right)+\cdots
フーリエ変換してみる
ここまできて、**x(t)をexpの項の足し合わせに変換するにはどうしたらいいの?**と言うステップになりました。それは意外と簡単で、周期が$T/n$の成分を取り出したい場合は以下の式でできます。
\int_{-T/2}^{T/2}\exp\left(-\frac{j2n\pi t}{T}\right)x(t)dt = \cdots+0+Tc_n+0+\cdots
先の直交性のおかげで、欲しい成分との内積をとるとその成分だけが取り出せます。これが教科書に載っているフーリエ変換の概要です。おそらく大学でこれを学ぶ際、関数の直交などはわりかし序盤で習うか他の科目で習うため、フーリエのときにを忘れてたりするんですよね。それが多くの技術者がフーリエ変換を詳しく説明できない要因かなぁと思ったり。。。
DFT
数式上でのフーリエ変換はわかりましたね。では次にDFT(離散フーリエ変換)をやります。何を離散にするのかと言うと、内積をとるときの積分です。
積分を離散化するのはそうたいしたことではないのです。時間tを離散的にして、積分はシグマで置き換えてしまいます。tはそれなりに細かくしないといけませんけどね。
というわけで、サンプリング周期を$d$で$N$点サンプリングするとき、$T = Nd, x = kd$となるので
d\sum_{k=0}^{N-1}\exp\left(\frac{-j2n\pi k}{N}\right)x(kd)
やってることは区分求積法と一緒です。そして$n$に対しても一次結合のためのシグマをつけると
d\sum_{n=-N/2}^{N/2-1}\sum_{k=0}^{N-1}\exp\left(\frac{-j2n\pi k}{N}\right)x(kd)\\
=d\sum_{n=0}^{N-1}\sum_{k=0}^{N-1}\exp\left(\frac{-j2n\pi k}{N}\right)x(kd)
ここで、スペクトルの番号(?)である$n$の和をとる範囲を勝手に0からN-1に変更しましたが、expの中身はn=Nで循環するので、特に問題ありません。次は行列演算の出番です。
\boldsymbol{x}=[x(0), x(d), \cdots, x(nd), \cdots]^T=[x_0, x_1, \cdots, x_n, \cdots]^T\\
\boldsymbol{W}=
\begin{bmatrix}
W_{0,0}&W_{0,1}&\cdots&W_{0,N-1}\\
W_{1,0}&W_{1,1}&\cdots&W_{1,N-1}\\
\vdots&\vdots&\vdots&\vdots\\
W_{n,0}&W_{n,1}&\cdots&W_{n,N-1}\\
\vdots&\vdots&\vdots&\vdots\\
W_{N-1,0}&W_{N-1,1}&\cdots&W_{N-1,N-1}
\end{bmatrix}\\
W_{n,k} = \exp\left(\frac{-j2\pi nk}{N}\right)
として
\boldsymbol{X} = d\boldsymbol{Wx}
と計算することができます。離散ステップのdですが、通常は付けないことが多いです。その代わりにスペクトルのパワーがN倍になります。
そして、先ほどnの範囲を0〜N-1に変更したので、スペクトルXもこの順番でもとまります。k=0から順番に定数項→共役スペクトル→実スペクトルの順になっていますので注意。
FFT
最後にFFT(Fast Fourier Transformation)です。FASTと言っているからにはそりゃ速いのですが、サンプル数が2の累乗である必要があります。ここからはステップを踏んで、簡単のためにN=2からスタートしましょう。このとき
\begin{bmatrix}
X_0\\
X_1
\end{bmatrix}
=
\begin{bmatrix}
1&1\\
1&\exp\left(\frac{-j2\pi 1*1}{2}\right)
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1
\end{bmatrix}
=
\begin{bmatrix}
1&1\\
1&-1
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1
\end{bmatrix}
=
\begin{bmatrix}
x_0+x_1\\
x_0-x_1
\end{bmatrix}
となります。次にN=4の時
\begin{align}
\begin{bmatrix}
X_0\\
X_1\\
X_2\\
X_3
\end{bmatrix}
&=
\begin{bmatrix}
1&1&1&1\\
1&\exp\left(\frac{-j2\pi 1*1}{4}\right)&\exp\left(\frac{-j2\pi 1*2}{4}\right)&\exp\left(\frac{-j2\pi 1*3}{4}\right)\\
1&\exp\left(\frac{-j2\pi 2*1}{4}\right)&\exp\left(\frac{-j2\pi 2*2}{4}\right)&\exp\left(\frac{-j2\pi 2*3}{4}\right)\\
1&\exp\left(\frac{-j2\pi 3*1}{4}\right)&\exp\left(\frac{-j2\pi 3*2}{4}\right)&\exp\left(\frac{-j2\pi 3*3}{4}\right)\\
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{bmatrix}\\
&=
\begin{bmatrix}
1&1&1&1\\
1&-j&-1&j\\
1&-1&1&-1\\
1&j&-1&-j\\
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{bmatrix}\\
&=
\begin{bmatrix}
x_0+x_1+x_2+x_3\\
x_0-jx_1-x_2+jx_3\\
x_0-x_1+x_2-x_3\\
x_0+jx_1-x_2-jx_3
\end{bmatrix}\\
&=
\begin{bmatrix}
(x_0+x_2)+(x_1+x_3)\\
1(x_0-x_2)-j(x_1-x_3)\\
(x_0+x_2)-(x_1+x_3)\\
1(x_0-x_2)+j(x_1-x_3)
\end{bmatrix}
\end{align}
意図的にカッコで括ってみました。N=2の時とN=4の出来上がった式を見ると、N=2の結果の形$x_0+x_2, x_0-x_2, x_1+x_3, x_1-x_3$がN=4の式に組み込まれていますね。添字が違うことはさておいて、今は式の形に注目してください。N=4の時のカッコを一つの文字とみなすと、係数はjで共通で、これもまた2つの数字の足しひきであることがわかります。
ここまでくると、N=2の時と組み合わせてこんなフローが描けます。
このように和と差をとる演算を繰り返し行うことでN=4のFFTの成分(順番が違うことは後述)が計算できます。
バタフライ演算
上の図の説明をしましょう。FFTをよくご存じの方はこの話題にいついくんだと思ったことでしょう。
上のフローをよく見ると、以下の2つの演算でのみ成り立っています。
矢印の形が蝶っぽいのでバタフライ演算と言います。左はaとbの和と差を出力し、右は差の方に重みWを付けたものです。
自作でFFTを作る時はこの2つの演算を行う関数を作っておき、入れ子で呼び出すことで作成できます。
閑話休題
話は戻ってFFTをNに関して一般化してみます。先に出てきたWは以下の通りで、添字をちょっと変えます。
W_N^{m}
=
W_{n,k}
=
\exp\left(\frac{-j2\pi nk}{N}\right)\\
m = nk
複素平面の単位円上を-m/N回転した数という意味で捉えてください。
N=4の時は
\boldsymbol{W}_4 =
\begin{bmatrix}
W_4^0&W_4^0&W_4^0&W_4^0\\
W_4^0&W_4^1&W_4^2&W_4^3\\
W_4^0&W_4^2&W_4^4&W_4^6\\
W_4^0&W_4^3&W_4^6&W_4^9\\
\end{bmatrix}
=
\begin{bmatrix}
1&1&1&1\\
1&W_4^1&W_4^2&W_4^3\\
1&W_4^2&W_4^4&W_4^6\\
1&W_4^3&W_4^2&W_4^1\\
\end{bmatrix}
となって、xと積を取ると
\begin{align}
\begin{bmatrix}
1&1&1&1\\
1&W_4^1&W_4^2&W_4^3\\
1&W_4^2&W_4^4&W_4^6\\
1&W_4^3&W_4^2&W_4^1\\
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{bmatrix}
&=
\begin{bmatrix}
1&1&1&1\\
1&W_4^1&-1&-W_4^1\\
1&-1&1&-1\\
1&-W_4^1&-1&W_4^1\\
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{bmatrix}\\
&=
\begin{bmatrix}
(x_0+x_2)+(x_1+x_3)\\
W_4^0(x_0-x_2)+W_4^1(x_1-x_3)\\
(x_0+x_2)-(x_1+x_3)\\
W_4^0(x_0-x_2)-W_4^1(x_1-x_3)
\end{bmatrix}
\end{align}
$W_4^3$は「単位円周上をマイナス方向に3/4回転」の意味なので、$W_2^1W_4^1$と同値で、$W_2^1=-1$なのでこのような結果になります。$W_4^0$は1なのですがあえてとっておきます。こうやって$W$の添字で係数を表現すると、N=4のバタフライ演算はこうかけます。
上に出てきた図と同じ意味ですが、Nが大きくなったときにこっちの方がみやすいです。
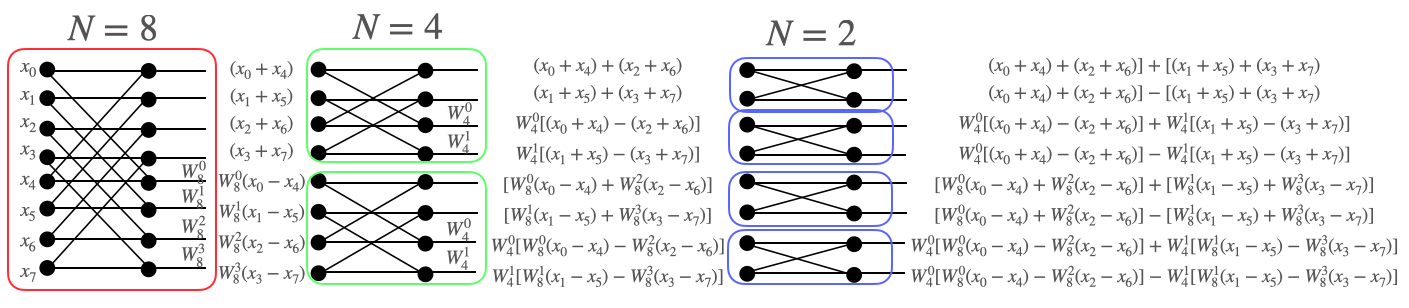
N=8でもやってみましょう。(大変)
\begin{bmatrix}
W_8^0&W_8^0&W_8^0&W_8^0&W_8^0&W_8^0&W_8^0&W_8^0\\
W_8^0&W_8^1&W_8^2&W_8^3&W_8^4&W_8^5&W_8^6&W_8^7\\
W_8^0&W_8^2&W_8^4&W_8^6&W_8^8&W_8^{10}&W_8^{12}&W_8^{14}\\
W_8^0&W_8^3&W_8^6&W_8^9&W_8^{12}&W_8^{15}&W_8^{18}&W_8^{21}\\
W_8^0&W_8^4&W_8^8&W_8^{12}&W_8^{16}&W_8^{20}&W_8^{24}&W_8^{28}\\
W_8^0&W_8^5&W_8^{10}&W_8^{15}&W_8^{20}&W_8^{25}&W_8^{30}&W_8^{35}\\
W_8^0&W_8^6&W_8^{12}&W_8^{18}&W_8^{24}&W_8^{30}&W_8^{36}&W_8^{42}\\
W_8^0&W_8^7&W_8^{14}&W_8^{21}&W_8^{28}&W_8^{35}&W_8^{42}&W_8^{49}
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3\\
x_4\\
x_5\\
x_6\\
x_7
\end{bmatrix}\\
=
\begin{bmatrix}
1&1&1&1&1&1&1&1\\
1&W_8^1&W_8^2&W_8^3&-1&-W_8^1&-W_8^2&-W_8^3\\
1&W_8^2&W_8^4&W_8^6&1&W_8^{2}&W_8^{4}&W_8^{6}\\
1&W_8^3&W_8^6&W_8^9&-1&-W_8^{3}&-W_8^{6}&-W_8^{9}\\
1&-1&1&-1&1&-1&1&-1\\
1&-W_8^1&W_8^2&-W_8^3&-1&W_8^1&-W_8^2&W_8^3\\
1&-W_8^2&W_8^4&-W_8^6&1&-W_8^{2}&W_8^{4}&-W_8^{6}\\
1&-W_8^3&W_8^6&-W_8^9&-1&W_8^{3}&-W_8^{6}&W_8^{9}\\
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
x_2\\
x_3\\
x_4\\
x_5\\
x_6\\
x_7
\end{bmatrix}\\
=
\begin{bmatrix}
x_0+x_1+x_2+x_3+x_4+x_5+x_6+x_7\\
x_0+W_8^{1}x_1+W_8^{2}x_2+W_8^{3}x_3-x_4-W_8^{1}x_5-W_8^{2}x_6-W_8^{3}x_7\\
x_0+W_8^{2}x_1+W_8^{4}x_2+W_8^{6}x_3+x_4+W_8^{2}x_5+W_8^{4}x_6+W_8^{6}x_7\\
x_0+W_8^{3}x_1+W_8^{6}x_2+W_8^{9}x_3-x_4-W_8^{3}x_5-W_8^{6}x_6-W_8^{9}x_7\\
x_0-x_1+x_2-x_3+x_4-x_5+x_6-x_7\\
x_0-W_8^{1}x_1+W_8^{2}x_2-W_8^{3}x_3-x_4+W_8^{1}x_5-W_8^{2}x_6+W_8^{3}x_7\\
x_0-W_8^{2}x_1+W_8^{4}x_2-W_8^{6}x_3+x_4-W_8^{2}x_5+W_8^{4}x_6-W_8^{6}x_7\\
x_0-W_8^{3}x_1+W_8^{6}x_2-W_8^{9}x_3-x_4+W_8^{3}x_5-W_8^{6}x_6+W_8^{9}x_7\\
\end{bmatrix}\\
=
\begin{bmatrix}
[(x_0+x_4)+(x_2+x_6)]+[(x_1+x_5)+(x_3+x_7)]\\
[W_8^{0}(x_0-x_4)+W_8^{2}(x_2-x_6)]+[W_8^{1}(x_1-x_5)+W_8^{3}(x_3-x_7)]\\
W_4^{0}[(x_0+x_4)-(x_2+x_6)]+W_4^{1}[(x_1+x_5)-(x_3+x_7)]\\
W_4^{0}[W_8^{0}(x_0-x_4)-W_8^{2}(x_2-x_6)]+W_4^{1}[W_8^{1}(x_1-x_5)-W_8^{3}(x_3-x_7)]\\
[(x_0+x_4)+(x_2+x_6)]-[(x_1+x_5)+(x_3+x_7)]\\
[W_8^{0}(x_0-x_4)+W_8^{2}(x_2-x_6)]-[W_8^{1}(x_1-x_5)+W_8^{3}(x_3-x_7)]\\
W_4^{0}[(x_0+x_4)-(x_2+x_6)]-W_4^{1}[(x_1+x_5)-(x_3+x_7)]\\
W_4^{0}[W_8^{0}(x_0-x_4)-W_8^{2}(x_2-x_6)]-W_4^{1}[W_8^{1}(x_1-x_5)-W_8^{3}(x_3-x_7)]
\end{bmatrix}\\
結構意図的な係数調整が入りますが、なんとかN=2とN=4の応用でかけそうです。
これを帰納的にやっていくと、Nがいくつであってもバタフライ演算で規則的に計算できることがわかります。
- 入力されたxを$x_m$と$x_{m+N/2}$でペアにして、重み付きバタフライに通します。この時の重みは$W_N^m$。
- 出力を上段と下段に分けてN/2サンプルの重み付きバタフライを2回行う。
この繰り返しでNがいくつでもFFTができます。N=8だとこんな感じ
N=2だけ重みなしのバタフライですが、重みありでやっても1をかけるだけなので同じ結果になります。ただし重みをかけるコストがかかるので、できれば重みありなしを使い分けた方が高速でしょう。
ビットリバース
これをみて結果の順番をみてください。$[x_0,x_1,x_2,x_3,x_4,x_5,x_6,x_7]$を入力して、出てきた結果は$[X_0,X_4,X_2,X_6,X_1,X_5,X_3,X_7]$になってますね。ここで添字を0から順番になるように入れ替える必要があります。ここで行う処理がビットリバースです。個人的にこれがFFTの最も肝の部分だと思います。
| 元の添字 | 元の添字のビット | 反転したビット | 入れ替え後の添字 |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 4 | 100 | 001 | 1 |
| 2 | 010 | 010 | 2 |
| 6 | 110 | 011 | 3 |
| 1 | 001 | 100 | 4 |
| 5 | 101 | 101 | 5 |
| 3 | 011 | 110 | 6 |
| 7 | 111 | 111 | 7 |
このようにビットを反転させて10進数に戻すと0から順に並びます。これ個人的感動ポイント。
計算量
普通のDFTをやろうと思ったら、各スペクトルの項と内積を取る計算をN^2回行う必要がありますが、FFTは上のバタフライの図でわかるように、N回のバタフライを$\log_2N$回行えばいいので合計で$N\log_2N$回の演算ですみます。
MATLABで組んでみた
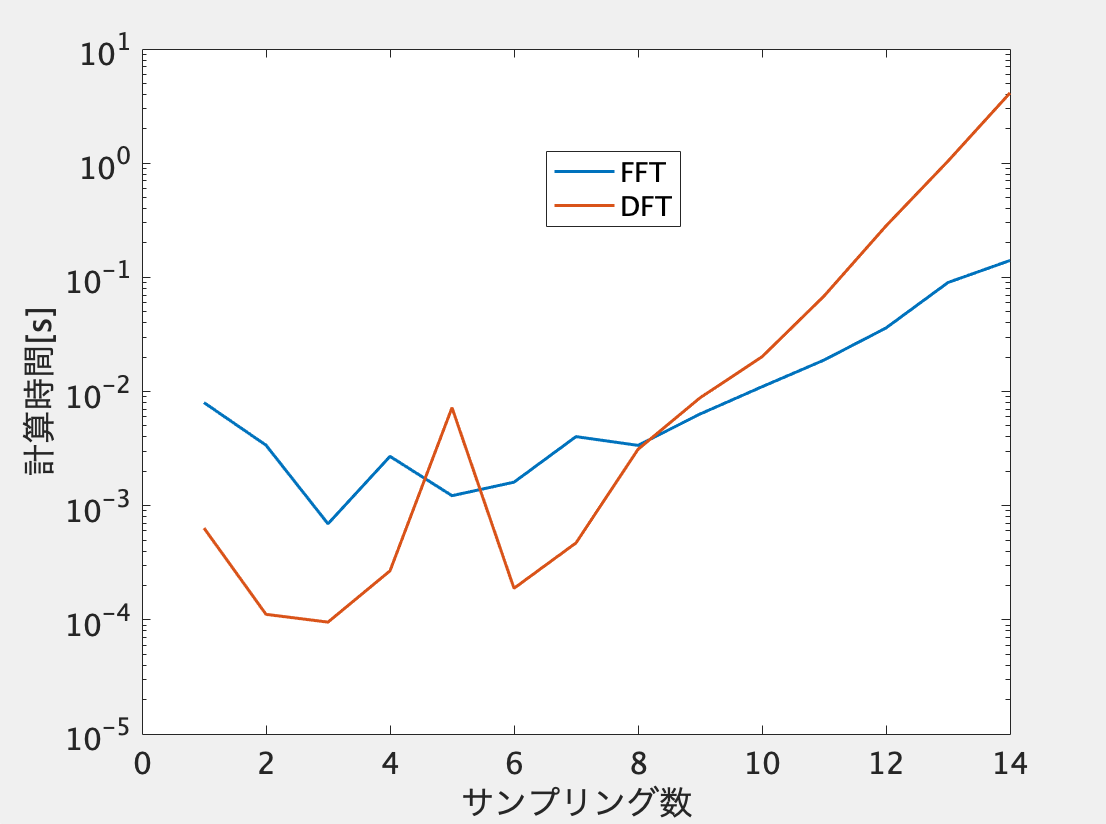
MATLABには元からFFT関数が用意されていて、Nによって様々なアルゴリズムを自動選択してくれるので、わざわざFFTを実装する意味はないのですが、なんの工夫もないDFTとFFTでどれくらい速度に違いがあるのかやってみます。
DFTの方はMATLABが得意としている行列計算をフルに使っているのでサンプル数が小さい時は速いですね。
しかしサンプル数が大きいとFFTがずば抜けて速いです。FFTも行列をうまく使うともっと速いかもしれませんね。
function y = myfft(x)
% 行ベクトルが入力された時のために次元を整理
x = (squeeze(x))';
% ループ計算の関数になげて、ビットリバース前の出力を受け取る
y = blockloop(x);
% ビットリバース後のインデックスを計算
idx = (1:length(y))';
idx = bitrevorder(idx);
% ビットリバース
y = y(idx);
end
%%
function y = blockloop(x)
% 信号の長さ
len = size(x,1);
% バタフライのループ回数
loopN = log2(len);
% 出力初期化。バタフライを1回も通さなければ入力がそのまま出てくる。
y = x;
% 図中横方向のループ数(N=8なら8=2^3なので3回)
for ic = 1:loopN
% 入力を分割した後の要素数
inlen = 2^(loopN-ic+1);
% 図中縦方向のループ数(N=8の最初の段だとN=8のバタフライを1回やるので1回、次の段ではN=4バタフライを2回やるので2回ループ)
for jc = 1:2^(ic-1)
y(inlen*(jc-1)+1:inlen*jc,:) = mybutterfly(y(inlen*(jc-1)+1:inlen*jc,:));
end
end
end
%% 重み付きバタフライ演算
function y = mybutterfly(x)
len = size(x,1);
% 重み
W = exp((-1i*2*pi/len)*(0:len/2-1)');
% 入力の上半分
xp = x(1:len/2,:);
% 入力の下半分
xm = x(len/2+1:end,:);
% 出力の上半分(足し算の方)
yp = xp + xm;
% 出力の下半分(引き算の方)
ym = W.*(xp - xm);
% 合体
y = [yp; ym];
end
function y = mydft(x)
% 信号の長さ
len = length(x);
% Wのインデックス
n = 0:1:len-1;
% W行列計算
W = exp(-2i*pi*n.*n'/len);
% 出力
y = W*(squeeze(x))';
end
最後に
フーリエ変換は画像処理や信号処理に限らず幅広く使われるもので、理系学科にいた方なら全員が知っているものだと思います。しかし意外と中身まで把握している人が少ないなぁと感じることもあり、自分もこの記事を書くまで知らなかったことがありました。フーリエ変換された後の複素数スペクトルの意味はなんなのか、絶対値の意味はなんなのか、出力される順番がなぜあんなことになっているのか、いろいろ合点がいきました。