ソフト設計に疎いMATLABユーザーがクラスについて最初にイメージを掴むための記事

背景

MATLABってどういう人が多く使っていると思いますか？

• 電気
• 機械
• ソフト
• 機械学習
• 金融
• 生産

パッと上げてもこれだけの利用分野が挙げられるように、MATLABは技術者・研究者の広くが利用している数少ない道具の一つだと思います。

なぜこんなに使われているのかというと、プログラムの敷居が超低いことが大きな要因ではないかと思います。比較的簡単と言われるPythonでさえ、グラフを出すためにはmatplotlibをインクルードし、numpyなどの算術ライブラリもインクルードし、、、結構面倒臭いですし、プログラミングを触ってこなかった人たちには何を使えばいいのかわからなくなってしまいます。(さらに無料ライブラリが豊富であるがゆえに、出てきた結果に誤りがない保証が難しいです。)
その点、標準でかなりの機能が使える上に、アドオンやツールボックスをGUIで管理し、コーディングも直感的なMATLABはプログラミング初心者にも非常に使いやすいため、これだけ普及しているのだと思います。

ただ、MATLABもベースはプログラミングであるので、プログラミング初心者には理解しづらい概念もあります。

その筆頭がクラスではないかと思います。

物理工学系の研究をする学生で、MATLABは書くけどもプログラミングには自信なしという人も多いはずです。そんな人に対して、オブジェクト指向のコーディングだとか、クラスヒエラルキーをちゃんとしようとか言っても、何のこっちゃよく分かりません。実際僕がそうでしたし。

この記事では、クラスの存在について、イメージを掴んでもらうための解説をしてみようと思います。

そもそもオブジェクト指向とは

クラスの上位概念としてオブジェクト指向というものがあります。まずはそれが何かについて説明します。(初学者に対するイメージ醸成を最優先とするので、間違いがある可能性があります。)

まず普通にコーディングしてみよう。

例えば、以下のプログラムを書きたいとします。

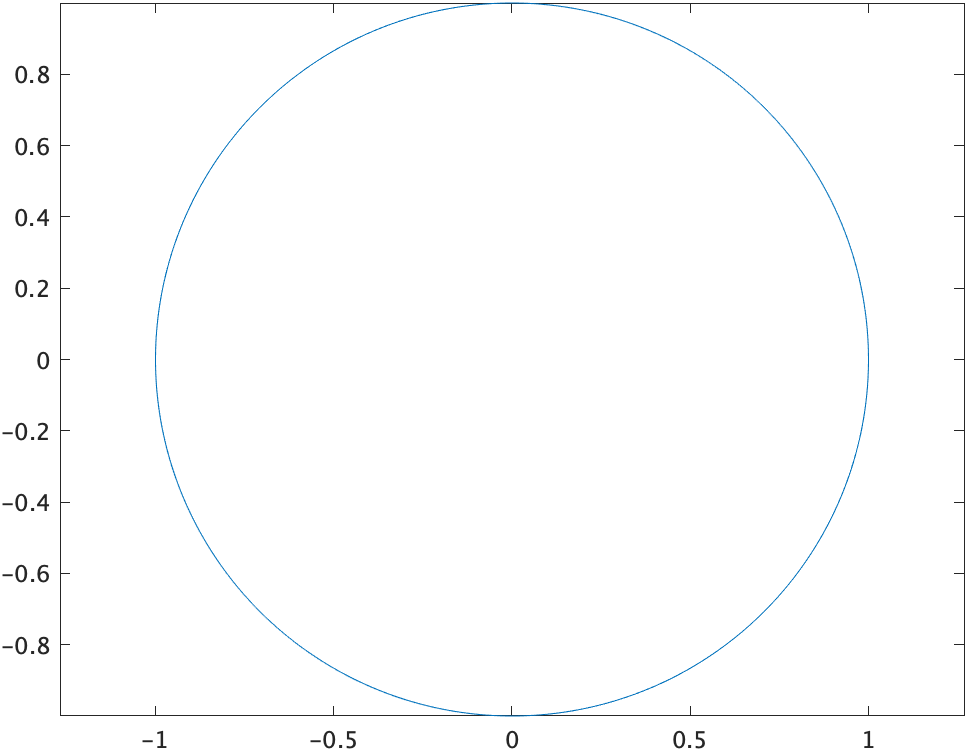
平面上の(0,0)の位置に半径1の円を描画する。

このようなコードになると思います。

ang = linspace(0,2*pi,360);
x = cos(ang);
y = sin(ang);
plot(x,y)

まあ普通ですね。
じゃあ少しレベルアップしてこうしてみましょう。

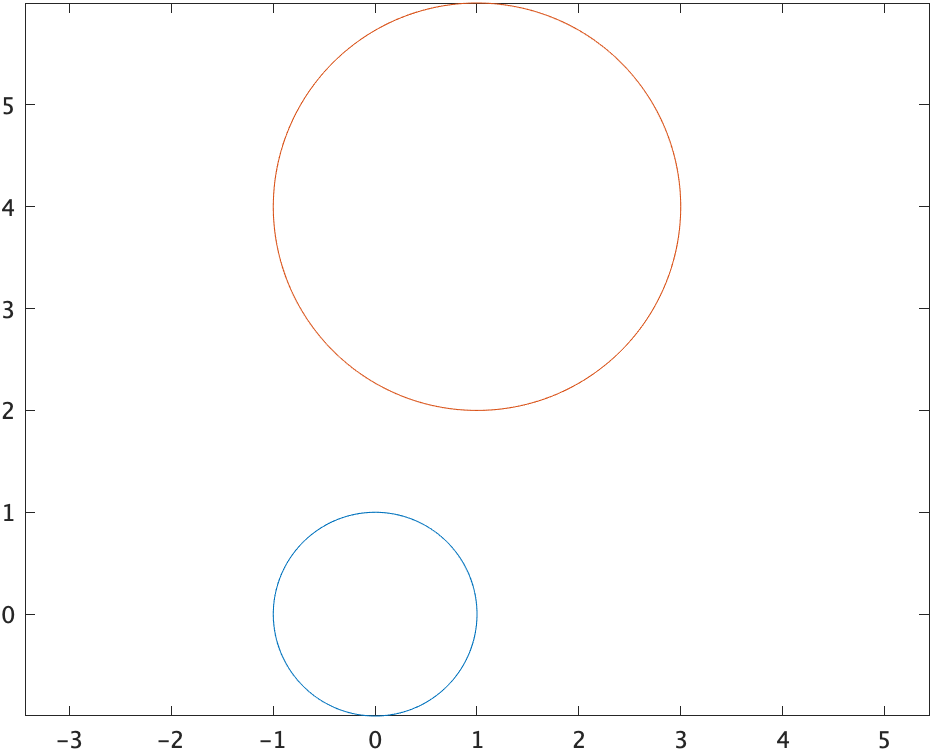
平面上の(0,0)と(1,4)の位置に、それぞれ半径1, 2の円を描画する。

まあこれもできるでしょう。こんな感じでしょうか。

% 平面上の(0,0)と(1,4)の位置に、それぞれ半径1, 2の円を描画する。
ang = linspace(0,2*pi,360);

x1 = cos(ang);
y1 = sin(ang); 

x2 = 2 * cos(ang) + 1;
y2 = 2 * sin(ang) + 4; 

plot(x1,y1)
hold on
plot(x2,y2)
hold off

関数にする

ここまでくると、「何回も同じ式を書くのめんどくさいなぁ。」と思いませんか？円を描くということを2回も書いているので、これが増えるとコーディングミスが起きるリスクがあるだけでなく、後からコードを見た人が読みづらいという弊害も出てきます。

そこで真っ先に思いつくのが、円の描画を関数にすることです。今の例で言うと、円の位置、半径、(描画対象の座標軸)を引数にする関数があればいいでしょう。

% 関数化する
pos1 = [0,0];
pos2 = [1,4];

r1 = 1;
r2 = 2;

figure
ax = axes(figure);
hold(ax,"on");
axis(ax,"equal");

DrawCircle(pos1,r1,ax);
DrawCircle(pos2,r2,ax);

% 円を描画する関数
function DrawCircle(pos, r, ax)
ang = linspace(0,2*pi,360);
x = r * cos(ang) + pos(1);
y = r * sin(ang) + pos(2); 
plot(ax,x,y)
end

結果は上と同じなので省略。

場合によってはposを行列形式にまとめてみたりして、コードの簡略化を図るでしょう。

関数化は神視点

関数化はコードを冗長にしないための基本的な手法で、オブジェクト指向においてもそのセンスは大事なものです。
しかし、ただ関数化をするだけだと、プログラムを理解する上で人間の感覚とずれることがあります。

それが全ての変数が神視点だと言うことです。

ある宗教では、神が森羅万象を創造したと考えられているらしいですが、関数化しただけのコードではまだその状態であり、神であるプログラマーは、全ての変数をいつでも変更できるが、その代わりに全ての変数に齟齬が発生しないように管理しなければならないという呪縛にかかってしまいます。

pos1,r1,円1は、互いに連携しているものでなければならないのに、神視点のプログラムでは、「pos1だけを変更して円1がそれについてこない」みたいなことが発生します。

pos,rを設定する
->円を描画する
->何かの都合でposを変更する。
->円の位置を知りたい事象が発生する。
->posを見てみるがそれは円の位置とは違うものになっている。

となることがあります。

オブジェクト指向

そこで神から脱却しましょう。神でいることは全てを支配している優越感に浸れる一方で、小さなミスが全体に響いてしまう可能性があります。プログラムが大きくなるほどその管理は大変で、いつかはミスが起きます。所詮あなたは人間なのです。

そこで、円にまつわるものは全て円に従属させるということができればいいのではないでしょうか。上位概念に円がいて、その構成要素としての半径・位置・描画関数がいる状態です。

こうすれば、円に対して「描画しろ!」と命令すれば、円がその処理を担当して描画をやってくれます。全てをプログラマーが管理する必要がなくなりますね。

• 円
  • 半径
  • 位置
  • 描画関数

分かりづらいかもしれないので言い換えると、「円を描くための材料に半径・位置・描画関数を持っているが、それをバラバラの状態で手に持っている状態」がただの関数化で、「円を描くための材料をいったん袋にまとめて、それを手に持っている状態」がオブジェクト指向です。

関数化だけ	オブジェクト指向設計
全てのものを一人で扱い切らないといけない。	意味のあるまとまりに分けて管理する。

クラス

まずは基本から

オブジェクト指向を達成するひとつの方法として、クラスを使う方法があります。
クラスとはまさに先の階層構造を記述するためのもので、MATLABではこんな感じの記載になります。

Circle.m

classdef Circle
    % 円クラス

    % 円がもっている変数
    properties 
        pos;
        r;
    end

    % 円がもっている関数
    methods
        function DrawCircle(obj,ax)
            ang = linspace(0,2*pi,360);
            x = obj.r * cos(ang) + obj.pos(1);
            y = obj.r * sin(ang) + obj.pos(2);
            plot(ax,x,y)
        end
    end
end

DrawCircleの引数にobjが追加されていますが、これは自身のパラメータを参照するために必要なので、先頭に入れておきます。これで、円自身が自分のパラメータを参照して描画するという処理ができ、外部からの干渉がなくなります。
メインプログラム内ではCircleクラスをもってこれば、それだけで円を描くための材料が全て揃います。

% 初歩的なクラス
circ1 = Circle;
circ2 = Circle;

circ1.pos = [0,0];
circ1.r = 1;

circ2.pos = [1,4];
circ2.r = 2;

figure
ax2 = axes(figure);
hold(ax2,"on");
axis(ax2,"equal");

circ1.DrawCircle(ax2);
circ2.DrawCircle(ax2);

これで、circ1のposを変更するなどの意図が明確になります。

少しレベルアップ

やっとオブジェクト指向の片鱗が見えてきたかと思います。ただここでこう言う疑問を抱きませんか？

「円に従属する変数にはなったけど、結局は勝手にいじれてしまうではないか!」

これを解消しましょう。つまり、勝手に円のパラメータを変更できないようにします。もっと言うとプログラマから円のパラメータが見えないようにします。

クラス定義のpropertiesにSetAccess=privateをつけて、円本人にしかプロパティを編集できなくします。

Circle_private_prop.m

classdef Circle_private_prop
    % 円クラス

    % 円がもっている変数
    properties (SetAccess = private)
        pos = [0,0]
        r = 1
    end

    % 円がもっている関数
    methods
        function DrawCircle(obj,ax)
            ang = linspace(0,2*pi,360);
            x = obj.r * cos(ang) + obj.pos(1);
            y = obj.r * sin(ang) + obj.pos(2);
            plot(ax,x,y)
        end
    end
end

こうすると、プログラム本体からpos, rは読み取り専用となり、編集できなくなります。

ちなみにpropertiesでpos = [0,0]などのようにするとクラスを定義した時の初期値を設定できます。

ここで、「編集できないならメインプログラムから位置を動かすとかできなくない?」って思うかもしれません。ここだけは少しめんどくさくて、円にパラメータを変更するための関数を設定しないといけません。神が円のパラメータを変更するのではなく、円自身が円のパラメータを変えると言う思想なので、円自体に値変更のための関数を持たせないといけません。

Circle_private_prop.m

classdef Circle_private_prop
    % 円クラス

    % 円がもっている変数
    properties (SetAccess = private)
        pos = [0,0]
        r = 1
    end

    % 円がもっている関数
    methods
        % 位置を変更してもらう
        function self = SetPos(obj,newPos)
            obj.pos = newPos;
        end
        
        % 半径を変更してもらう
        function self = SetR(obj,newR)
            obj.r = newR;
        end
        
        % 描画してもらう
        function DrawCircle(obj,ax)
            ang = linspace(0,2*pi,360);
            x = obj.r * cos(ang) + obj.pos(1);
            y = obj.r * sin(ang) + obj.pos(2);
            plot(ax,x,y)
        end
    end
end

circ3 = Circle_private_prop;
circ4 = Circle_private_prop;

circ3 = circ3.SetPos([0,0]);
circ3 = circ3.SetR(1);

circ4 = circ4.SetPos([1,4]);
circ4 = circ4.SetR(2);

figure
ax3 = axes(figure);
hold(ax3,"on");
axis(ax3,"equal");

circ3.DrawCircle(ax3);
circ4.DrawCircle(ax3);

もう少しレベルアップ。プロットもクラスに。

あと一つ変えてみましょう。今のクラスでは、パラメータは円の持ち物になりましたが、プロットそのものがメインプログラムのものであり、さらに半径や位置が変更されてもプロットがアップデートされません。

まずはパラメータにラインを追加します。

Circle_private_prop.m

properties (SetAccess = private)
    pos = [0,0]
    r = 1
    linePlot
end

次にコンストラクタを設定します。別にこれでなくてもいいのですが、勉強のために説明します。
コンストラクタとは、クラスが呼び出された時に自動で呼ばれる関数で、引数が必要な初期化などに使われます。
書き方はシンプルで、クラス名と同じ名前の関数を設定するだけです。

Circle_private_prop.m

% コンストラクタ
function obj = Circle_private_prop(ax)
    obj.linePlot = plot(ax,0,0);
end

今回は、描画先の座標系に初期プロットを入れておきます。
これで、描画の時はこのプロットをいじればいいことになります。

パラメータが変更されたらそれに応じてプロットも変更されるように変更すると、こんな感じになります。

Circle_private_prop.m

classdef Circle_private_prop
    % 円クラス

    % 円がもっている変数
    properties (SetAccess = private)
        pos = [0,0]
        r = 1
        linePlot
    end

    % 円がもっている関数
    methods
        % コンストラクタ
        function obj = Circle_private_prop(ax)
            obj.linePlot = plot(ax,0,0);
        end

        % 位置を変更してもらう
        function obj = SetPos(obj,newPos)
            obj.pos = newPos;
            obj.UpdateCircle();
        end
        
        % 半径を変更してもらう
        function obj = SetR(obj,newR)
            obj.r = newR;
            obj.UpdateCircle();
        end

        % 描画を更新してもらう
        function UpdateCircle(obj)
            ang = linspace(0,2*pi,360);
            x = obj.r * cos(ang) + obj.pos(1);
            y = obj.r * sin(ang) + obj.pos(2);

            obj.linePlot.XData = x;
            obj.linePlot.YData = y;
        end
    end
end

figure
ax3 = axes(figure);
hold(ax3,"on");
axis(ax3,"equal");

circ3 = Circle_private_prop(ax3);
circ4 = Circle_private_prop(ax3);

circ3 = circ3.SetPos([0,0]);
circ3 = circ3.SetR(1);

circ4 = circ4.SetPos([1,4]);
circ4 = circ4.SetR(2);

これで円のパラメータを変えれば勝手に描画も値も更新されて、外部から不要な編集をされない、オブジェクト指向のプログラムが書けます。
本当はもっと多機能なのですが、これくらいで初歩的な操作はいいかと思います。

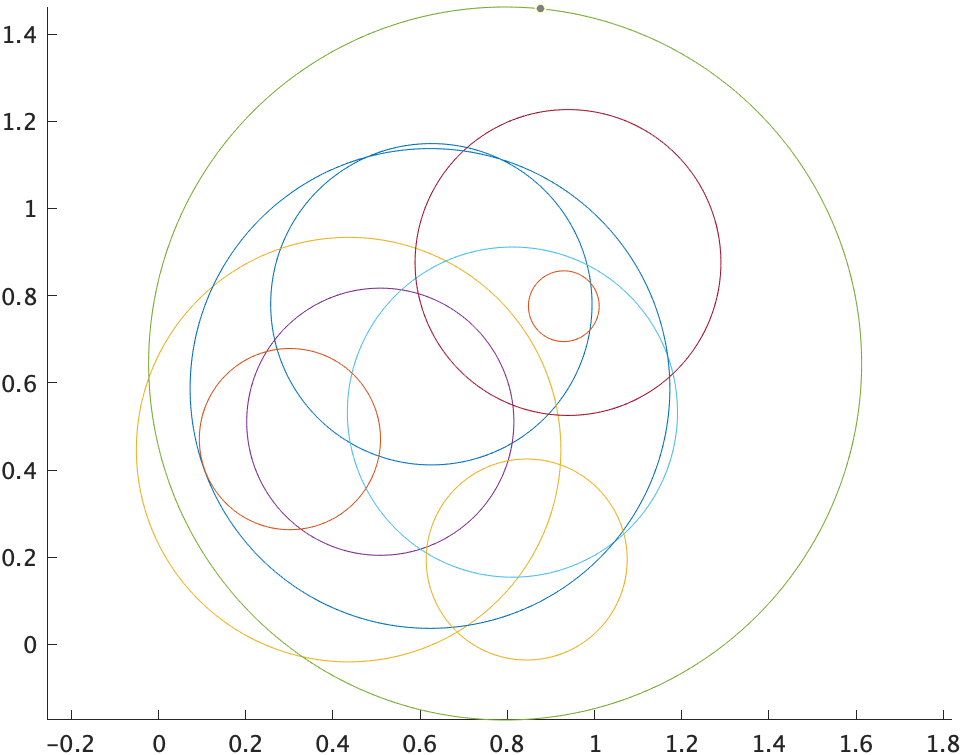
ここまでくると、これだけのコードで円の描画ができてしまいます。

figure
ax = axes(figure);
hold(ax,"on");
axis(ax,"equal");

circles = [];
for idx = 1:10
    circles = [circles, Circle_private_prop(ax)];
    newR = abs(rand(1))
    newPos = rand(1,2)
    circles(end) = circles(end).SetR(newR);
    circles(end) = circles(end).SetPos(newPos);
end

ここまでのまとめ

本当はもっとやれることもあるのですが、ソフト開発者ではない技術者にとってはこれで十分ではないかと思います。他にやったほうがいいことについては

• 円自身しか呼び出さない、メインコードからは呼んでほしくない関数もprivateにしておく。
• 関数やパラメータの型指定(argumentsを調べれば出てきます)

などでしょうか。とにかくオブジェクト指向において大事なことは、

• あなたは神ではない。
• ある事物(今回でいえば円)に従属しているパラメータはその事物の持ち物として、レイヤーをはっきりさせる。
• 外からいじってほしくないパラメータはprivateにして、メソッドを仲介しない限り変更不可能にする。

ということです。

使い所の例

ここまで読んだだけだとこう思うかもしれません。

「なるほど。では自分は物体の自由落下運動について研究しているから、りんごクラスを作って質量とか位置とかを管理すればいくつでもりんごを落とせるわけだな。」

正しいです。実際に簡単な検証であればこれで十分でしょう。しかし、りんごはあくまでりんご自身のパラメータを持つだけであって、りんごが落下運動させているわけではありません。みなさんご存知の通り、落下は2つ以上の質量を持つ物体同士の引き合いなので、ひとつの物体のクラスではどうにもなりません。

そこでクラスの別の使い方として、システムを表現するクラスをつくることがあります。

りんごクラスはとりあえずこんな感じにしておいて

Apple.m

classdef Apple
    %UNTITLED2 このクラスの概要をここに記述
    %   詳細説明をここに記述

    properties (SetAccess = private)
        might double = 1;
        pos (1,2) double = [0,0];
    end

    methods
        function obj = SetMight(obj,newMight)
            obj.might = newMight;
        end

        function obj = SetPos(obj,newPos)
            obj.pos = newPos;
        end
    end
end

万有引力クラスをこのようにして、万有引力の働く空間の中にりんごクラスをもっておきます。

UniversalGravitation.m

classdef UniversalGravitation

    properties (SetAccess = private)
        apples (1,:) Apple
        G = 6.67259e-11;
    end

    methods
        % 指定した数のりんごを空間に召喚
        function obj = UniversalGravitation(numApple)
            obj.apples(1,numApple) = Apple;
        end

        % りんごの質量を設定する
        function obj = SetAppleMight(obj, newMights)
            if numel(obj.apples) ~= numel(newMights)
                error("りんごの数と質量ベクトルの要素数が一致しません。")
            end

            for idx = 1:numel(obj.apples)
                obj.apples(idx) = obj.apples(idx).SetMight(newMights(idx));
            end
        end

        % りんごの位置を設定する
        function obj = SetApplePos(obj, newPoses)
            if numel(obj.apples) ~= size(newPoses,1)
                error("りんごの数と位置ベクトルの要素数が一致しません。")
            end

            for idx = 1:numel(obj.apples)
                obj.apples(idx) = obj.apples(idx).SetPos(newPoses(idx,:));
            end
        end
    end
end

これでメインコードで以下のようにすると、りんごを10個もった、万有引力を解析させるためのクラスが出来上がります。引力が発生する空間にりんごをとりあえず召喚したとイメージですね。

Newton.m

ug = UniversalGravitation(10);
ug = ug.SetAppleMight(abs(rand(1,10)) * 10);
ug = ug.SetApplePos(rand(10,2) * 10);

あとは適当に万有引力の式とかを関数にして組み込めば、万有引力の計算はこのクラスにやらせておいて、メインコードではその結果を使って何かを分析する、という棲み分けができます。

全てのものをクラスにしないといけないわけではないですが、コードが煩雑になればなるほど、こういうレイヤーの整理は重要です。ある種のシミュレーションをやるようなものであれば特にクラスが生かされるかもしれません。

これでもレイヤーがうまくいかないことがあり、そんな時は継承などの機能を使うのですが、そこからはまた別の記事にするかもしれません。
次回記事: https://qiita.com/tommyecguitar/items/8021940e93ed2e9044d9