初めての記事投稿です。
初めてだと勝手がわからなくて、記事が出来上がるまで時間がかかりますよね。
今も緊張しているせいか、書いては消して、書いては消して、を繰り返してます。
この文を書くまでに一体何行の文を消したことか。
ま、1回なんですけど。
初めまして、とみーです。
初投稿はコスタス配列について書こうと思います。
コスタス配列が初耳だという方にもわかるように、その有用性や魅力を解説しようと思います。
私は別に数学者でもなんでもないので、正確に書くというよりは、イメージが伝わればなぁと思います。
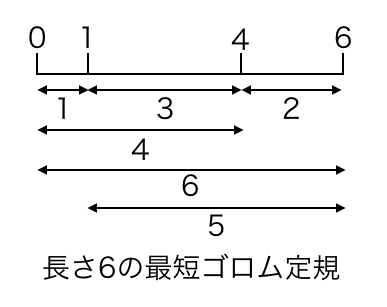
ゴロム定規
コスタス配列の前に、その簡易版の概念としてゴロム定規を紹介します。
ゴロム定規は整数列の一種で、以下の定義があります。
ゴロム定規(ゴロムじょうぎ、英: Golomb ruler)とは、想像上の定規の上で一連の整数位置にマークを配置し、任意のマークの対の距離がどれをとっても等しくならないものをいう。
この**「任意のマークの対の距離がどれをとっても等しくならない」**ことがゴロム定規の最大の性質であり、このあと説明するコスタス配列にもつながります。
例として0,1,4,6を用います。数直線上に0,1,4,6をとり、数字の間の距離を全通り書いてみます。
0,1,4,6だけで1から6までの距離を測ることができるだけでなく、測り方が1通りのみです。
この時、ゴロム定規の数字の数を次数、最大数6と最小数0の差を長さといい、最大数と最小数の差と、定規の長さが等しいものを**「完全ゴロム定規」**といい、5次以上の完全ゴロム定規は存在しないことが証明されています。
何がすごいんや
ゴロム定規の素晴らしいところを、少し小難しく表現してみると、こんな感じ。
「定規を水平に並行移動しても、元の定規と2つ以上の目盛りが重なることはない」
当たり前ですよね。あらゆる数列の中で、ずれに対する重なりが最小ということです。
信号に応用してみましょう。
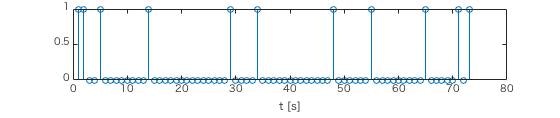
例えばこんな信号を考えてみます。
g=[0, 1, 4, 13, 28, 33, 47, 54, 64, 70, 72]\\
s(t)=
\left\{
\begin{array}{ll}
1 & t=g_n\\
0 & otherwise
\end{array}
\right.
時間$t$がゴロム定規の数列と一致した時に振幅1の出力するインパルス関数です。
波形はこんな感じ。
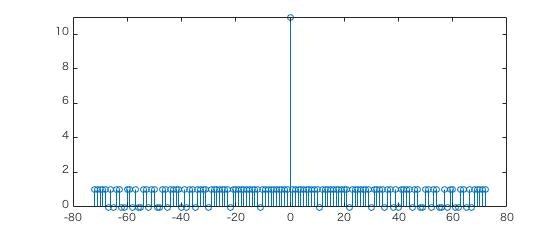
先ほど記述した**「ずれに対する重なりが小さい」**という性質は、自己相関を取るとはっきりわかります。
こちらが自己相関です。ただし、ここでは正規化を行わない自己相関とします。
**「定規を水平に並行移動しても、元の定規と2つ以上の目盛りが重なることはない」**わけなので、シフトゼロ以外は自己相関係数が1より大きくはなりません。
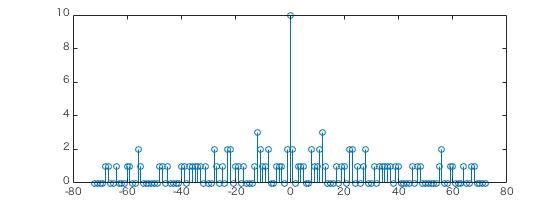
よくわからない人のために比較も用意しましょう。ランダムな時間に振幅1を出力するインパルスの場合、自己相関はこうなります。(平等のためにインパルスの数はゴロム定規と同じにします)
ランダムだと小さかったり大きかったりバラバラですし、シフトゼロの地点以外にどでかいピークが来ない保証もないです。普通ランダムって、こういった重複をなくすために使われがちですが、ランダムに勝る数列が存在するとは感動です。
コスタス配列
ゴロム定規は1次元で、**「任意のマークの対の距離がどれをとっても等しくならない」**数列でした。
2次元に拡張したくないっすかこれ。
というわけで、ゴロム定規の2次元拡張verが、**「コスタス配列」**です。
ゴロム定規では数直線で考えましたが、2次元拡張ということで平面上の格子点を考えます。
ゴロム定規が**「任意のマークの対の距離がどれをとっても等しくならない」**なら、コスタス配列はこうです。
コスタス配列の任意の2点間のベクトルが、どれをとっても等しくならない
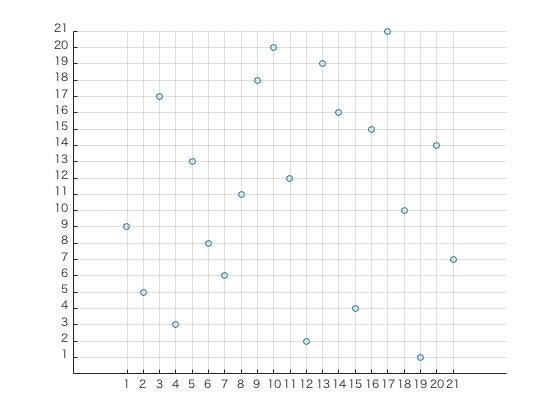
さっそく登場してもらいましょう。こちらがコスタス配列さんです。
さすがに2点間のベクトルを全部書き出すのは疲れるので、そこは信じてください。ゴロム定規と異なるのは、点数が21に対して、横軸も縦軸も21です。ゴロム定規との共通点は、横軸も縦軸も同じ数字を取りません(あるxに対してyは一点のみ。逆もしかり)。
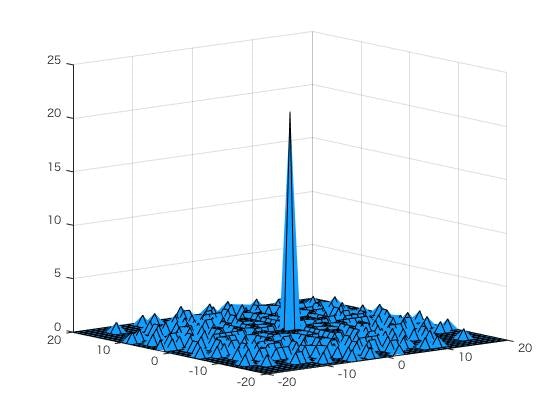
さあ自己相関を取ってみましょう。これも該当する座標でz=1を取ると思ってください。
はい来ました。やはりシフト量ゼロの地点以外の自己相関係数は1以下です。
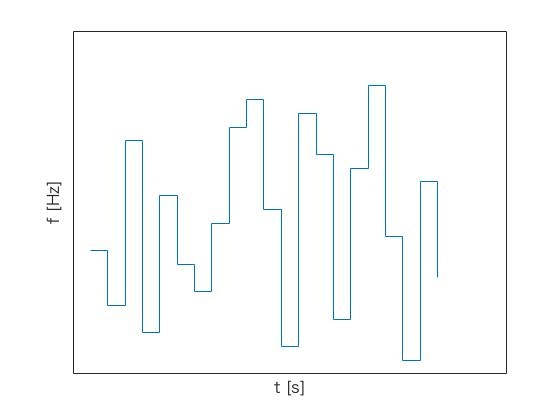
でもそんなパルスなんて使わねえよ。というあなた。コスタス配列にこんな軸名をつけてみましょう。
プロットを階段にしました。
多くの皆さんには見慣れない軸だと思いますが、電波屋さんにはよく知れたグラフで、変調の周波数を時間軸にプロットしたものにします。自分自身レーダ屋さんなので、レーダの原理を簡単に交えてこの配列の有用性を説明します。
レーダの原理超簡易版
レーダ(RADAR)とは、電波の反射を利用して、物体の速度、方位、距離を測定するものです。このうち、速度(相対速度)を測定するのに、ドップラー効果を使います。また、距離を測定するのに電波が跳ね返ってくるまでの時間差を用います。そして、レーダの利点は自分の送信信号を処理に使えるところです。(通信とかだとそうはいかないですよね)
この時間差とドップラー効果による周波数変動を読むのに、先のグラフを使います。
よく使う変調にこんなものがあります。
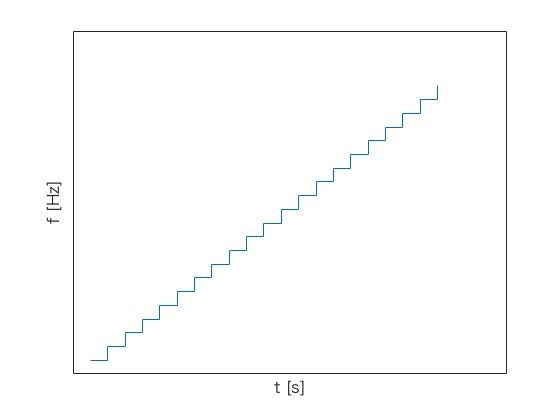
方式によって様々ですが、多くのレーダは時間とともに周波数を上げていく変調パターンを繰り返します。
これだと自己相関がこうなってしまいます。
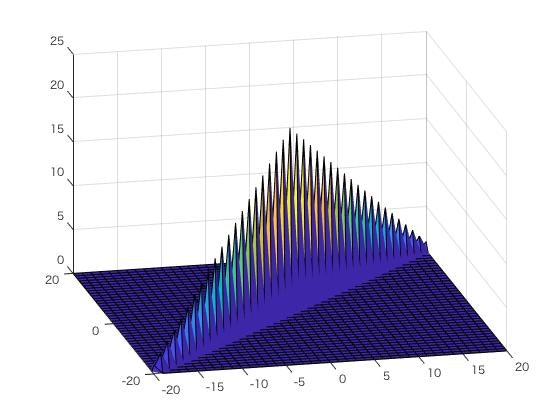
これじゃあどこがピークなのか不確実ですよね。(もちろん方位を測ることもレーダの役目なので、頭ごなしにこの変調をディスりませんよ)
自己相関でピークが読み取りやすいということは、送信と受信に周波数と時間のシフトがあっても、送信と受信の相関を取ることで、正確にシフト量を検知できるということです。特にコスタス配列は、ドップラーと反射波の遅延を利用するレーダにとって、とても便利なものなのです。特に、方位を気にしなくて、標的の数の少ない海底の地形探査ではよく使われます。
まとめ
今回はゴロム定規とコスタス配列を紹介しました。ランダムよりも優れた相関の特性を持っており、何かのシフト量を測定したいときなどに有用なのではないかと思います。
ランダムよりも規則性のないゴロム定規とコスタス配列ですが、難点があります。それは
大きいサイズの配列を見つけるのが超大変
実はコスタス配列は29以下の自然数しか見つかっていません。NP困難(wikipedia)の問題の一つです。もっと巨大なものが見つかれば、通信などにも応用できるかも知れないですね。