XDWYVTDAU244RVKT1C3LDN6 LNRV,IQDABECZKJI.VYPWVORQCWE6ET.ZK9IAL.Z1.MM
いきなり謎の文章で始めましたが、これがエニグマ暗号です。第二次世界大戦中にドイツ軍が使用していた、強力な暗号です。イギリスの数学者アラン・チューリングらによって解読され、ドイツは情報をごっそり取られて敗北するわけです。WWIIの終わりには数学者の功績があったんですね。
エニグマ暗号の概要
エニグマ暗号は、ある文字を別の文字に入れ替える形式の暗号です。それ以前の暗号は、入れ替える文字の組み合わせが1通りでした。A->H、B->Nと言うように、文字の組み合わせが決まっているため、頻度分析などで解析ができてしまいます。
しかしエニグマ暗号は文字を1つ打つたびに文字の変換が変わってしまうため、それまで最強だった頻度分析で歯が立たなくなってしまいます。
試しにエニグマでAを連打した時と、それまでの暗号(カエサル暗号)で同じことをした時を比べてみましょう
- カエサル暗号→JJJJJJJJJJJJJJJJJJJJ
- エニグマ暗号→GKGVMDNLZXSYFPKSRJOX
カエサル暗号は明らかに何かを連打していますね。これだと、英語でよく出るアルファベットAやS、逆にあまり出てこないXやZなどで頻度の差が生まれます。対してエニグマは、1文字ごとに変換される文字が変わるので、文字を連打していることすらよくわかりません。これを解いたポーランドとチューリングすごい。
エニグマの仕組み
エニグマは以下の5つの回路構成で成り立っています。
- プラグボード
- スクランブラー x 3
- リフレクタ
信号の流れは以下の図のような感じです。
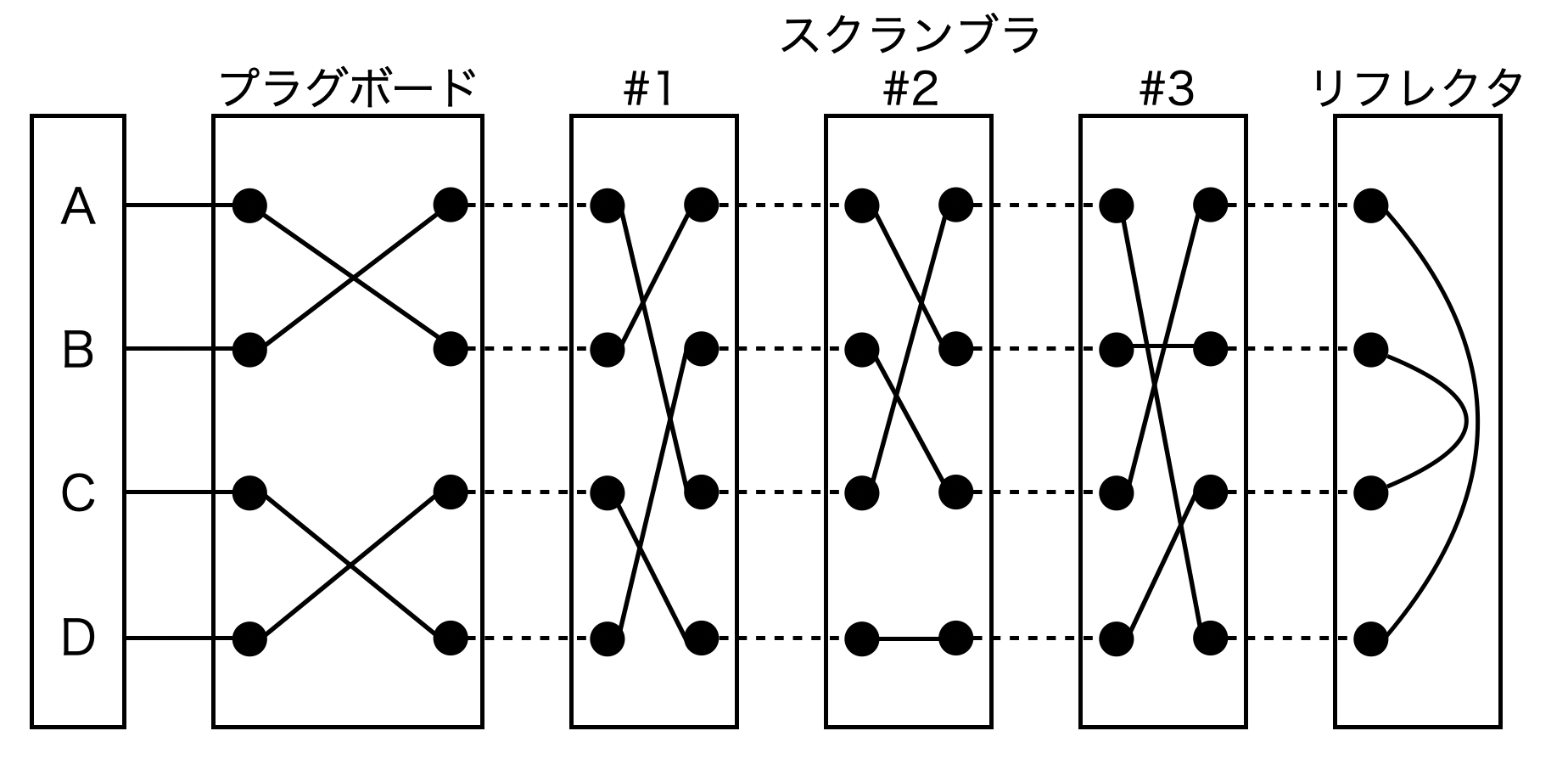 プラグボードは2つの文字をケーブルで繋ぎ、その2角文字を入れ替えることができるボードです。スクランブラは円盤状の文字並べ替え装置で、回転することで文字の入れ替え方を変えることができます。リフレクタは信号を折り返すもので、ここでも文字の入れ替えができます。使用者が設定するのは、**プラグボードと~~リフレクタの配線~~(リフレクタは固定の場合が多いようです)、使うスクランブラの組み合わせ、スクランブラの初期位置**です。
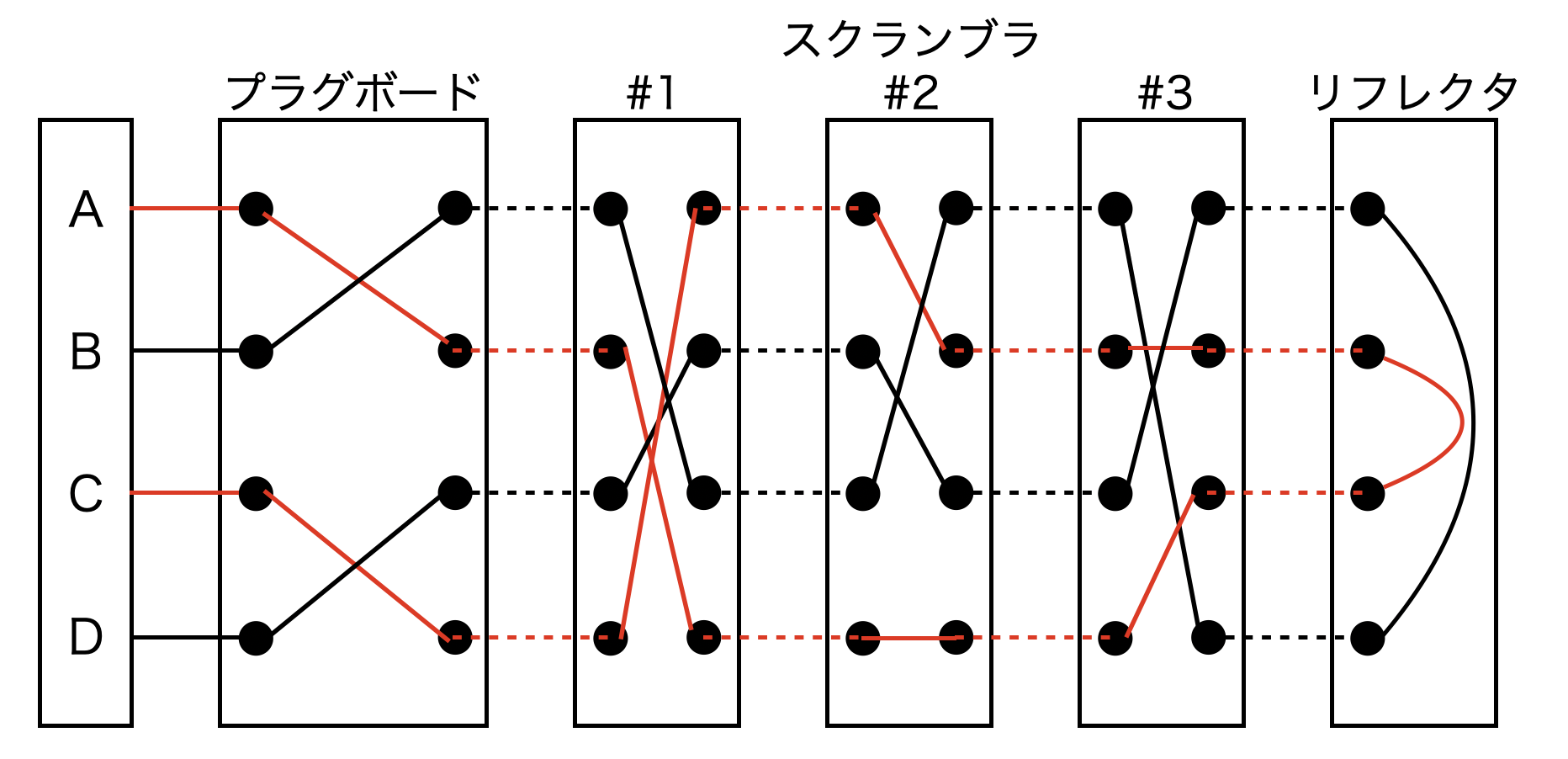
上の図だとABCDの4文字が入力できますので、試しにAを入力してみると数のように信号が流れ、Dが出力されます。逆にDを入力するとAに復号できます。
プラグボードは2つの文字をケーブルで繋ぎ、その2角文字を入れ替えることができるボードです。スクランブラは円盤状の文字並べ替え装置で、回転することで文字の入れ替え方を変えることができます。リフレクタは信号を折り返すもので、ここでも文字の入れ替えができます。使用者が設定するのは、**プラグボードと~~リフレクタの配線~~(リフレクタは固定の場合が多いようです)、使うスクランブラの組み合わせ、スクランブラの初期位置**です。
上の図だとABCDの4文字が入力できますので、試しにAを入力してみると数のように信号が流れ、Dが出力されます。逆にDを入力するとAに復号できます。
 これだけだとカエサル暗号と同じですが、エニグマは文字を打つごとにスクランブラが回転します。回転規則は、
- #1→1文字うつごとに1シフト
- #2→4文字うつごとに1シフト
- #3→16文字うつごとに1シフト
となります。nこの文字が入力可能な時は
- #1→1文字うつごとに1シフト
- #2→$n$文字うつごとに1シフト
- #3→$n^2$文字うつごとに1シフト
となります。したがって上の図でもう一回Aを入力すると、スクランブラ#1が回転し、Cが出力されます。
これだけだとカエサル暗号と同じですが、エニグマは文字を打つごとにスクランブラが回転します。回転規則は、
- #1→1文字うつごとに1シフト
- #2→4文字うつごとに1シフト
- #3→16文字うつごとに1シフト
となります。nこの文字が入力可能な時は
- #1→1文字うつごとに1シフト
- #2→$n$文字うつごとに1シフト
- #3→$n^2$文字うつごとに1シフト
となります。したがって上の図でもう一回Aを入力すると、スクランブラ#1が回転し、Cが出力されます。
 # 線形代数的なエニグマ
エニグマを線形代数的にとらえてみましょう。
nこの入力がありk番目のキーが押されたときの入力行ベクトルを以下のように定義します。
# 線形代数的なエニグマ
エニグマを線形代数的にとらえてみましょう。
nこの入力がありk番目のキーが押されたときの入力行ベクトルを以下のように定義します。
s=[0, 0, \cdots, 0,1,0,\cdots]\\
s(j) =
\left\{
\begin{array}{cc}
1,&j=k\\
0,&j\neq k
\end{array}
\right.
前節のようにABCDのキーがあり、Cが入力された場合は$s=[0, 0, 1, 0]$となります。
置換行列
プラグボードとスクランブラ、リフレクタは文字を並べ替える操作を行います。これは置換行列を使うことで線形代数的に処理できます。置換行列は各列、各行に1つずつ1をもち、それ以外は0の行列で、例えば4次の置換行列
P =
\begin{bmatrix}
0&0&1&0\\
1&0&0&0\\
0&0&0&1\\
0&1&0&0
\end{bmatrix}
を、適当な行列$A$の右から作用させると、
AP=
\begin{bmatrix}
a_1&b_1&c_1&d_1\\
a_2&b_2&c_2&d_2\\
a_3&b_3&c_3&d_3\\
a_4&b_4&c_4&d_4
\end{bmatrix}
\begin{bmatrix}
0&0&1&0\\
1&0&0&0\\
0&0&0&1\\
0&1&0&0
\end{bmatrix}
=
\begin{bmatrix}
b_1&d_1&a_1&c_1\\
b_2&d_2&a_2&c_2\\
b_3&d_3&a_3&c_3\\
b_4&d_4&a_4&c_4
\end{bmatrix}
のように、列の並べ替えを行うことができます。また、左から作用させると
PB=
\begin{bmatrix}
0&0&1&0\\
1&0&0&0\\
0&0&0&1\\
0&1&0&0
\end{bmatrix}
\begin{bmatrix}
a_1&a_2&a_3&a_4\\
b_1&b_2&b_3&b_4\\
c_1&c_2&c_3&c_4\\
d_1&d_2&d_3&d_4
\end{bmatrix}
=
\begin{bmatrix}
c_1&c_2&c_3&c_4\\
a_1&a_2&a_3&a_4\\
d_1&d_2&d_3&d_4\\
b_1&b_2&b_3&b_4
\end{bmatrix}
のように行の並べ替えができます。ランダムで置換行列を作るならいいですが、手動で作るときは列の入れ替えか行の入れ替えかよく考えないとミスるので注意です。
スクランブラの入出力の性質上当たり前ですが、$P^{-1}=P^T$です。
プラグボード、スクランブラ、リフレクタは全て置換行列によって表現できますが、それぞれに少し特徴があるので説明していきます。
プラグボードとリフレクタ
プラグボードとリフレクタは、入力$x$を出力$y$と入れ替え、入力$y$を出力$x$に入れ替えます。スクランブラは並べ替えだったのに対して、プラグボードとリフレクタは入れ替えなので、
P=P^{-1}
である必要があります。プログラム上は、単位行列の列か行の入れ替えによって置換行列を作成し、一度入れ替えた列、行を再び入れ替えることのないようにします。
スクランブラ
スクランブラは逆行列と元の行列が等しい必要がない行列で、プログラム上は単位行列の列や行の並べ替えで作成します。
スクランブラの面倒なところは回転するところで、行列的には、スクランブラが回る=行列の成分を行方向と列方向に1ずらすことに対応します。MATLABではcircshiftで対処できますが、行列計算する場合はスクランブラ行列の左右から置換行列を作用させればOKです。
この「スクランブラが回転する」仕様のせいで、MATLAB上でもforループを使って1文字ごとに変換していくしかないのですが、そんなに重い処理じゃないので勘弁しましょう。
線形代数での暗号化式
いよいよ暗号化します。
- 使用する文字種の数を決定します。アルファベットなら26です。
- 文を決めます。先に決定した文字だけを使ってください。
- 行列計算で処理するため、文を1文ずつベクトル化します。前述した通り、文字種の数だけ0が並び、特定の要素のみが1となる行ベクトルとします。列ベクトルでもいいですが、あとの行列の乗算方向が逆になります。
- 文字種の数とサイズが等しい置換行列各種を作ります。プラグボードとリフレクタは上記の注意点があります。
- 1文字ずつ以下の式に従って変換する。(1文字づつ計算する理由はスクランブラが回る処理が入るため。)
C={\bf s}PS_1S_2S_3RS_3^{-1}S_2^{-1}S_1^{-1}P
※1文字ごとにスクランブラを回転させる処理を行う。
コード
MATLABでエニグマ暗号機を作ってみます。
スクランブラ行列作成
前述の通り、スクランブラ行列は単位行列の列の並べ替えで作成できます。Levelはエニグマに打ち込める文字の種類の数で、アルファベットだとLevel=26となります。
function ScrambleMat = ScrambleGenerator(Level)
% 単位行列
I = eye(Level);
% 1〜Levelの整数をランダムで並べ替え
RND = randperm(Level);
% 単位行列の列を並べ替え
ScrambleMat = I(:,RND);
end
リフレクタ、プラグボード行列作成
リフレクタとプラグボードは行列上同じ処理を行います。スクランブラとは違って列の入れ替えであることに注意。
function ReflMat = ReflectorGenerator(Level)
% 単位行列
I = eye(Level);
% 1〜Levelの整数をランダムで並べ替え
RND = randperm(Level);
% 入れ替える列を選択。PreRNDで選んだ列とPostRNDで選んだ列を入れ替える。
PreRND = RND(1:Level/2);
PostRND = RND(Level/2+1:Level);
% 入れ替え処理
ReflMat = I;
ReflMat(:,PreRND) = ReflMat(:,PostRND);
ReflMat(:,PostRND) = I(:,PreRND);
end
初期設定
文字種を設定し、各行列を作成、保存する。
clear
close all
%% 文字種(アルファベットと少しの記号と数字を設定)
PlaneAlphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ. ,-1234567890';
LenAlph = length(PlaneAlphabet);
%% 各行列を作成
PlugBoard = ReflectorGenerator(LenAlph);
FirstScramble = ScrambleGenerator(LenAlph);
SecondScramble = ScrambleGenerator(LenAlph);
ThirdScramble = ScrambleGenerator(LenAlph);
Reflector = ReflectorGenerator(LenAlph);
I = eye(LenAlph);
%% 保存
save('I.mat','I')
save('PlaneAlphabet.mat','PlaneAlphabet')
save('PlugBoard.mat','PlugBoard')
save('FirstScramble.mat','FirstScramble')
save('SecondScramble.mat','SecondScramble')
save('ThirdScramble.mat','ThirdScramble')
save('Reflector.mat','Reflector')
暗号化
文を設定し、暗号化します。まずは前半部分
clear
close all
%% 文を設定。(今は大文字に変換している)
PlaneStr = 'May the force be with you.';
PlaneStr = upper(PlaneStr);
LenStrings = length(PlaneStr);
%% スクランブラの初期回転数を設定
ShiftScrOne = 5;
ShiftScrSnd = 10;
ShiftScrThd = 20;
%% 行列を読み込み
load('I.mat')
load('FirstScramble.mat')
load('PlaneAlphabet.mat')
load('PlugBoard.mat')
load('Reflector.mat')
load('SecondScramble.mat')
load('ThirdScramble.mat')
%% スクランブラを初期位置まで回転
FirstScramble = circshift(FirstScramble,[ShiftScrOne ShiftScrOne]);
SecondScramble = circshift(SecondScramble,[ShiftScrOne ShiftScrOne]);
ThirdScramble = circshift(ThirdScramble,[ShiftScrOne ShiftScrOne]);
スクランブラの初期位置も設定項目に含まれるので、とりあえず入れてみました。そして後半
%% エンコード(デコードもできます)
% 文字をベクトル化して処理する。
CodeIdx = [];
for idx = 1:LenStrings
% idx番目の文字が、文字種内の何番目にあるかを探索
k = strfind(PlaneAlphabet,PlaneStr(idx));
StrIdx = k;
% 文字をベクトル化
StrIdxMat = I(StrIdx,:);
% エンコードするための行列式を前もって計算(みにくいから)
Encord = PlugBoard*FirstScramble*SecondScramble*ThirdScramble*Reflector/...
ThirdScramble/SecondScramble/FirstScramble*PlugBoard;
% 入力のベクトルに乗算し、結果を連結する。
CodeIdx = [CodeIdx;StrIdxMat*Encord];
% スクランブラ#1は毎回シフトさせる
FirstScramble = circshift(FirstScramble,[1 1]);
% スクランブラ#2は#1が一回転するごとにシフト
if mod(idx,length(PlaneAlphabet)) == 0
SecondScramble = circshift(SecondScramble,[1 1]);
% スクランブラ#3は#2が一回転するごとにシフト
if mod(idx,length(PlaneAlphabet)^2) == 0
ThirdScramble = circshift(ThirdScramble,[1 1]);
end
end
end
% 暗号化されたベクトルの各行の何番目に1があるか探索する。(文字種内の何番目の文字に変換されたか)
[CodeStrIdx,~,~] = find(CodeIdx');
% ベクトルを文字化する
Code = PlaneAlphabet(CodeStrIdx)
暗号化の例
エニグマ暗号は各文字に対して
C={\bf s}PS_1S_2S_3RS_3^{-1}S_2^{-1}S_1^{-1}P
の処理でかけると説明しました。これを複合しようと思うと、行列部分の逆行列を右から作用させればいいのですが、すると、
C={\bf s}[PS_1S_2S_3RS_3^{-1}S_2^{-1}S_1^{-1}P][PS_1S_2S_3RS_3^{-1}S_2^{-1}S_1^{-1}P]
となり、全く同じ行列が2回並ぶことになります。(当たり前ですが)
なので、設定が同じエニグマ機がある場合、暗号文をもう一度通すと復号されると言う性質があります。
私の環境では"MAY THE FORCE BE WITH YOU"は"33O0YGMYI-X8A,ZJLKR2K,WBP9"に変換されましたが、この暗号文をもう一度通すと"MAY THE FORCE BE WITH YOU"が得られ、復号ができます。
長めの文にもチャレンジしましょう。今度は小文字も許すように設定します。
原文は以下から抜粋
New York Timesの記事より
暗号文
qKnzLGqu,AJjp9RyVURYL2SRg42QPADw5e,bJIVRxxPxMQMEgMz2k24K7Iz9vr4-6NVenlzdTXNO6iJUUoMTc5qIN22IbfGFl6DStRqCXs4-y87nkzvtoT.THyFW3kQ7XBt.kSB-1ej4tBL5EIwZdKyGjJ3lZrF6PuhE-ufrYkxnlC3kAuCiV18C6DjMItuPqZM,.RmGxAqFKT CbUZhjZHstHGAzrAbp.SYpNdOnQVWyUmsf5XICAWH1Y984Ibz8JKHd,
復号文
The good news for Europe is that the worst of the pandemic is beginning to ease. This week deaths in Italy hit a nearly two-month low. And the German leader Angela Merkel announced that schools, day care centers and restaurants would reopen in the next few days.
ちゃんと復号できました。"とか'の記号がある場合は、プログラム内で適切に処理をしないと、バグるかもしれません。
まとめ
エニグマ暗号機を線形代数的に捉えることで、プログラムの実装がかなり楽になりました。このプログラムだと、任意のスクランブラやプラグボードなどを使用できますし、文字もアルファベット大文字に限らず小文字も使えるような拡張や記号も使えます。
実際のドイツ軍はスクランブラを5つくらいに増やして使っていたようですが、その改造も簡単ですね。
参考
