前回はアンテナの最低限の基礎とレーダの構成について説明しました。
前回のおさらいです。
- レーダは「距離」「速度」「方位」を推定、測定する。
- アンテナは基本的には広い方向に電波をばらまく。
- 小さい波源からの電波は球面波で伝搬する。
- アレーアンテナは、位相差、振幅差をつけることで、任意の方位の電波をカットできる。
これくらいを覚えていれば十分でしょう。今回はいよいよ「距離」と「速度」を推定します。
今回のトピックスは以下のとおり
- 基本的な数式
- パルスレーダとCWレーダ
- パルス方式
- FMCW方式
- FCM方式
- まとめ
基本的な数式
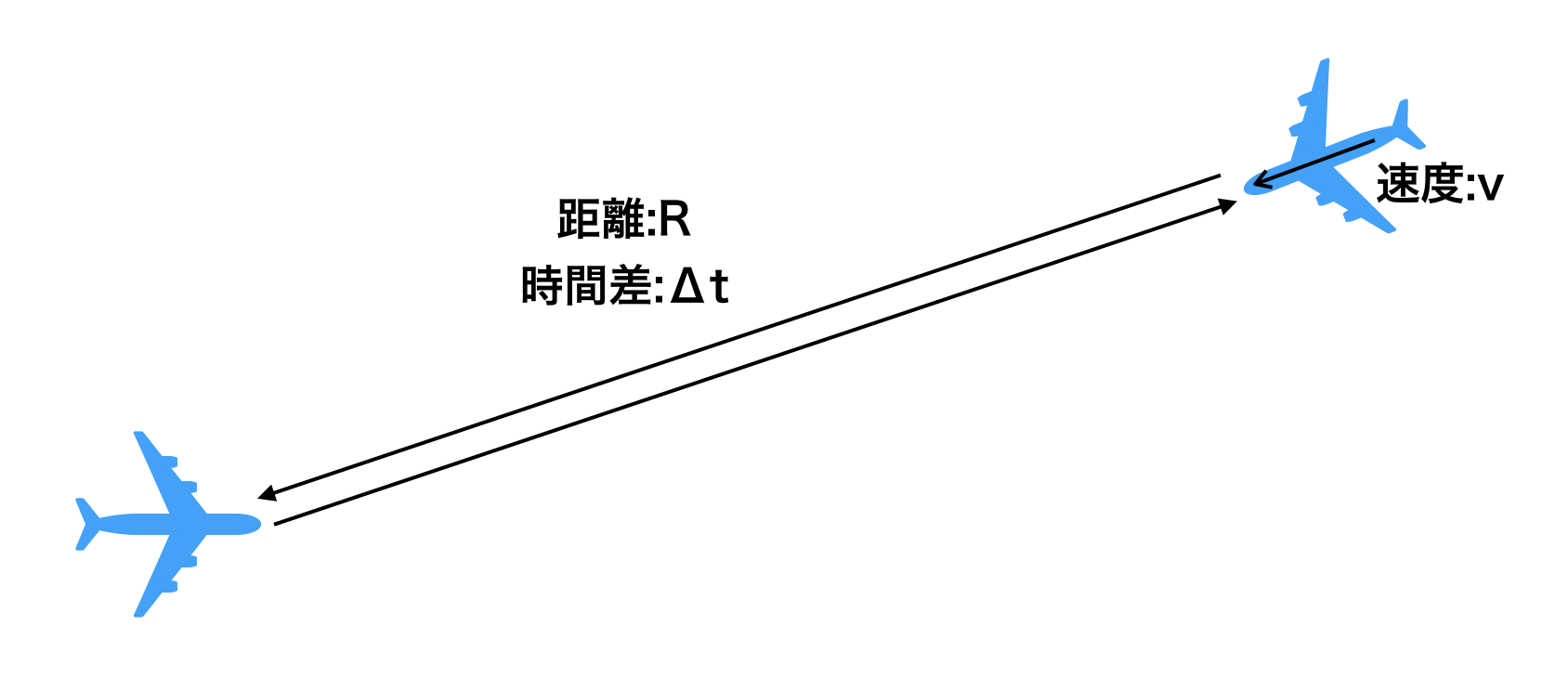
左の飛行機は中心周波数$f_c$の電波を放射し、その波が距離$R$の地点を速度$v$の飛行機で反射し、$\Delta t$の時間遅れののちに受信されます。
距離測定
距離$R$は直感的にすぐ計算できそうですね。光速は$c$なので以下の式が成り立ちます。
$$R=\cfrac{c\Delta t}{2}$$
距離=速度×時間の式ですね。分母の2は時間差$\Delta t$が往復分の時間差のためについています。
速度測定
速度についてはドップラー効果による周波数のシフトを利用します。電波は伝搬する媒質がなく光速で伝搬するので、光速度不変の原理を用います。その時のドップラーによる周波数の式は以下のようになります。
$$f_d=\left[1-\cfrac{v}{c}\right]f_c$$
$f_d$はドップラー効果によって変化し、自分の元に帰ってくる周波数です。
ここで皆さんこんな感想を抱くかもしれません。
「高校物理で解けるんか。意外と大したことないなぁ。」
そうです。大したことないんです。
ただ今説明した状況をグラフにしてみましょう。まず、レーダは周波数$f_c$を放射しますので、放射した電波の周波数の時間変化は以下のようになります。
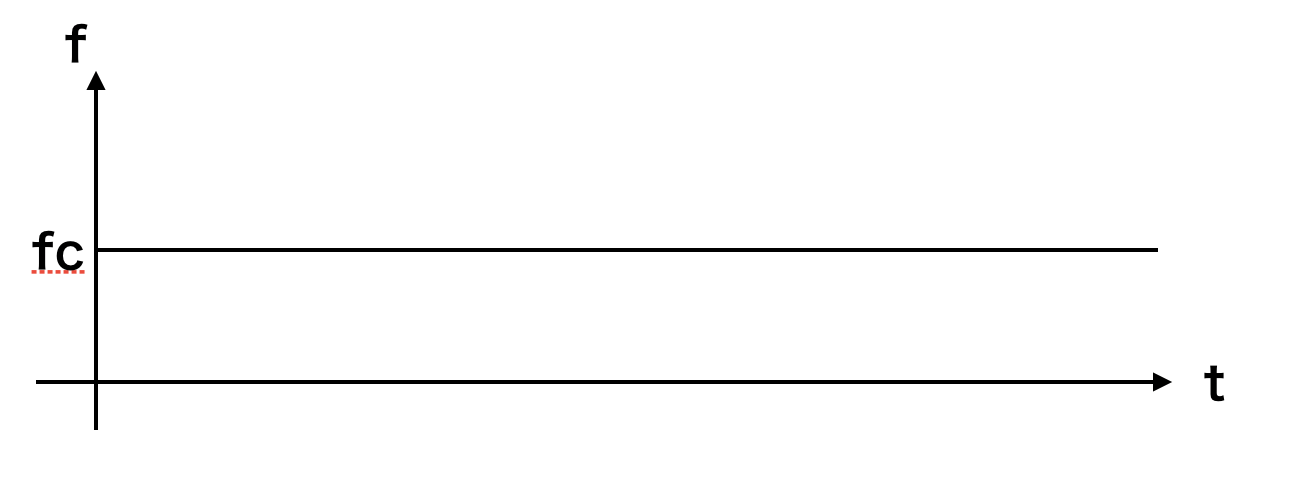
跳ね返ってきた電波は、時間$\Delta t$遅れ、周波数は$f_d$になっていますので、受信電波の周波数はこんな感じ。

大問題発生です。$f_d$は読めますが、$\Delta t$が読めません。困った!!!
これを解決する基本的な方法が次のセクションです。
パルスレーダとCWレーダ
前セクションで、$\Delta t$を読み寄れない原因は、簡単に言うと2とおりあります。
- ずっと電波を出しているので、トリガーになるものがない。
- 周波数が一定なので、トリガーになるものがない。
1を解決するのがパルスレーダ、2を解決するのがCWレーダと言うわけです。パルスレーダはその名の通り、電波を出したり止めたりして、電波のon/offでトリガーを作る方式です。CWレーダのCWとは、continuous waveの略で、定常波のことです。電波でっぱなし。その代わり、周波数をスウィープしてトリガーをつけるやり方です。
パルス方式
パルスレーダは、時間のトリガーを電波のon/offで作る方法です。送信信号の周波数はこんな感じになります。
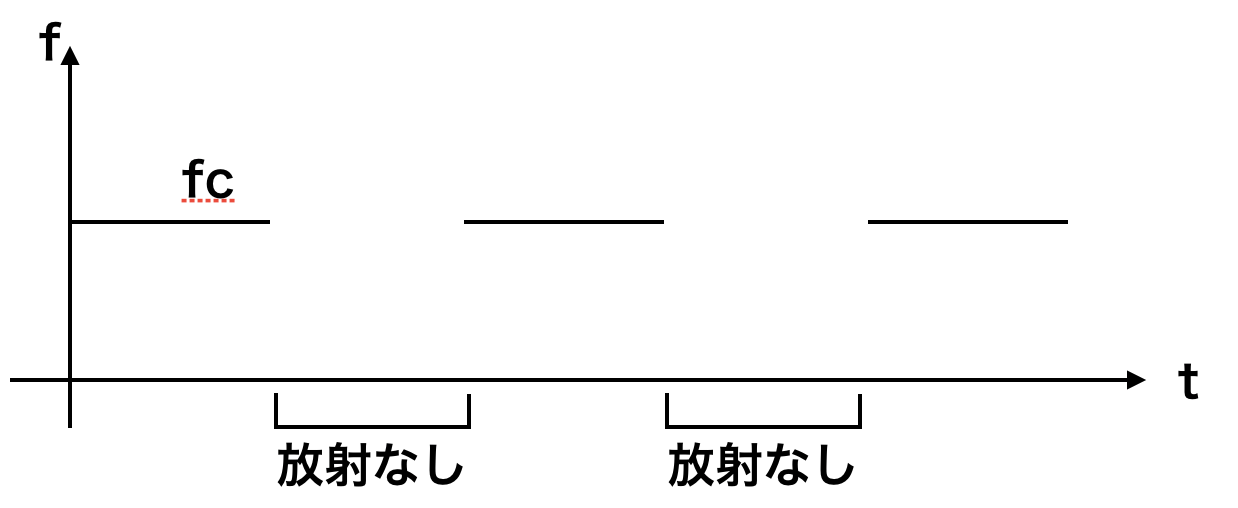
正直これは知識がなく、そこまで詳しく書けないのですが、アルフリズムとしては前セクションの式をそのまま使います。
なので、詳細な説明は省きます。
パルスレーダのメリットとしては、距離→時間差、速度→周波数と、2つの目的値を2つの物理量で観測することで、近距離の検知が安定していることです。デメリットは、放射しない時間があるので、時間の無駄遣いであること、高周波信号をそのまま処理するために高いクロック周波数が求められることなどがあります。
FMCW方式
FMCWはfrequency modulated continuous waveのことで、周波数変調された定常波です。ざっくりすぎる定義です。一般的にFMCWと言えばこんな変調を指します。
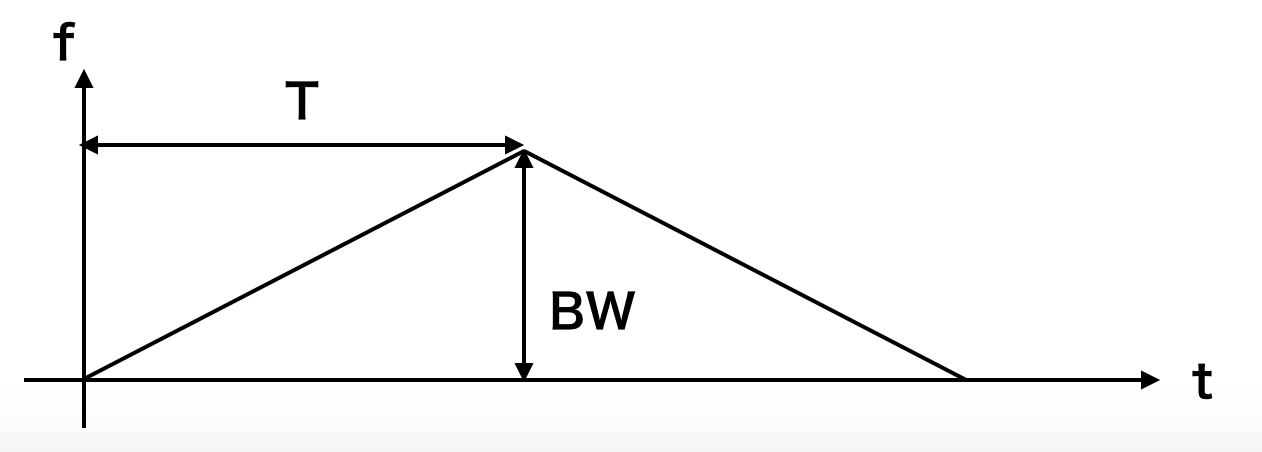
周期$2T$の間に周波数を増加、減少させる変調を永遠に繰り返します。時間遅れとドップラーシフトが起きるので、反射波はこのようになって受信されます。
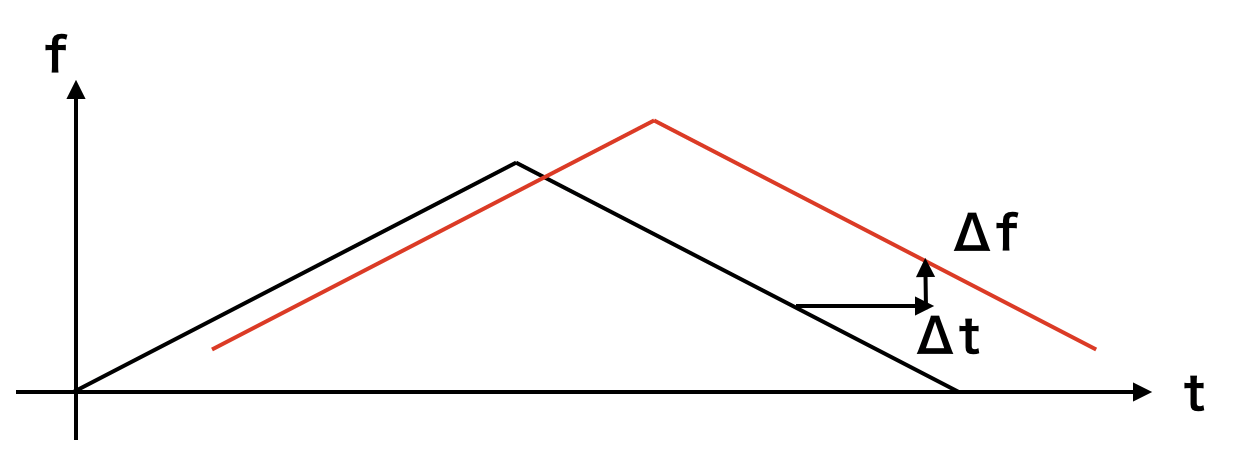
ここで少し考えるとこう思いませんか?
「山の頂点を読まないと$\Delta t$と$\Delta f$読めんくない?」
そんなことないんですよこれが。FMCW方式では、この反射波をそのまま扱いません。放射した波と受信した波の差をとり絶対値とし、ビート信号と言われる波を作ります。それがこちら。
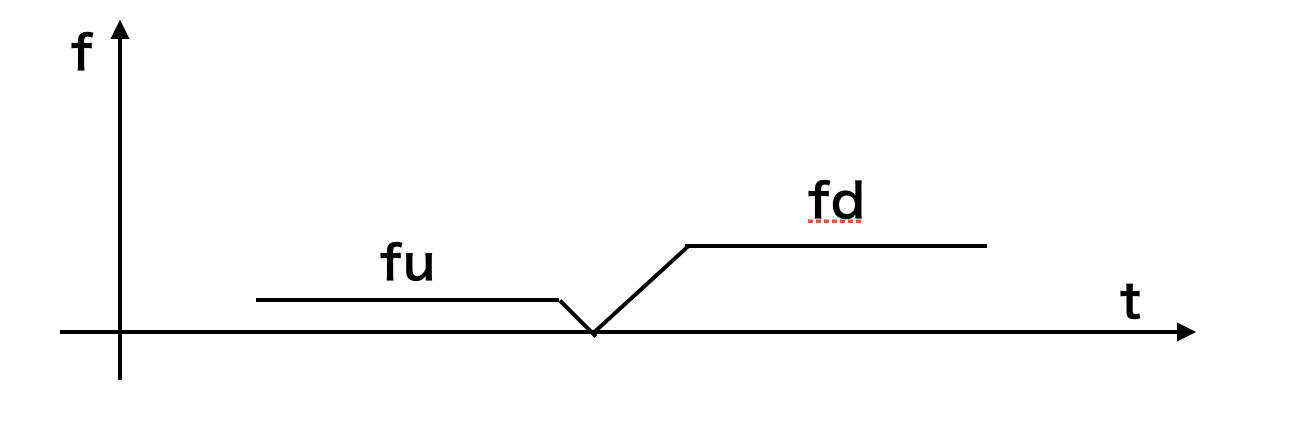
ちなみに実際はFFTでビート信号を解析しています。ドップラーシフトしても変調の傾きは変わらないので、$f_u$と$f_d$の波になります。ビート信号は放射、受信した波より周波数が低いため、高周波で処理する必要がなく、回路的に嬉しいのです。
さあここで、基本に戻りましょう。送信した信号が周波数上昇中のとき、その周波数はこんな式でした。
$$f=\cfrac{BW}{T}t$$
受信する波は、周波数が$f_d$で$\Delta t$遅れているので
$$f-\cfrac{v}{c}f=\cfrac{BW}{T}(t-\Delta t)$$
ここで、$\frac{v}{c}f$ですが、帯域幅BWが中心周波数$f_c$に対して小さい場合、$\lambda_cv$とすることができます。送信と受信の差をとると、
$$f_u=\cfrac{BW}{T}\Delta t-\lambda_cv$$
となります。これが上図の$f_u$です。同じことを周波数減少中の波で計算すると、
$$f_d=\cfrac{BW}{T}\Delta t+\lambda_cv$$
となります。もうお分かりですかね、$\Delta t$と$v$はこのようにして計算できます。
$$\Delta t=\cfrac{T}{2BW}\cfrac{f_u+f_d}{2}$$
$$v=\cfrac{f_d-f_u}{2\lambda_c}$$
時間差から距離はわかるので、距離$R$は
$$R=\cfrac{cT}{4BW}\cfrac{f_u+f_d}{2}$$
となります。CW方式のいいところは、ずっと電波を出しているので、平均化によるノイズ除去などがしやすいこと、ビート信号を用いるので高周波のクロックがいらないことにあります。デメリットとしては、距離と速度を周波数だけで計算するため、1つの対象物に対して2つの周波数が必要なところです。複数のターゲットがある場合、「周波数のペアがどれなのか」と言う問題を解かなければいけません。まあ中心周波数に対して$f_u$と$f_d$は対称なので、そう難しくはないですが、周波数が被ってしまうと分離しなきゃいけないので、大変です。
FCM方式
FCMは現在最も主流であろう方式で、FMCWの周波数ペアリング問題を解決したものです。基本はCW系ですが、周波数の変調が違います。
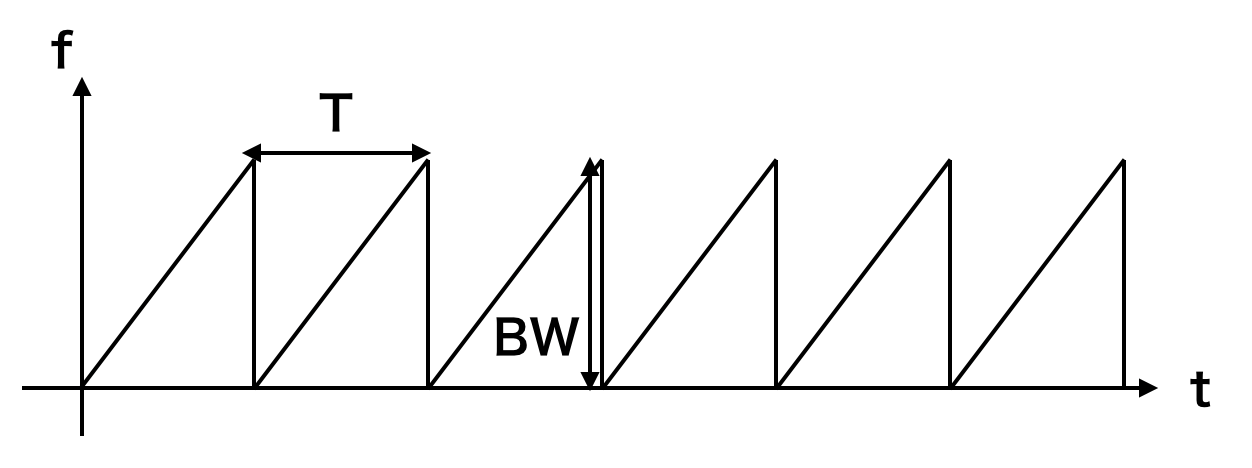
FMCWの変調周期よりも圧倒的に短い周期で変調し、周波数上昇の変調しかありません。反射してきた波はこのようになります。変調周期が非常に短いので、ドップラーによる周波数変化は無視できるほど小さいとします。
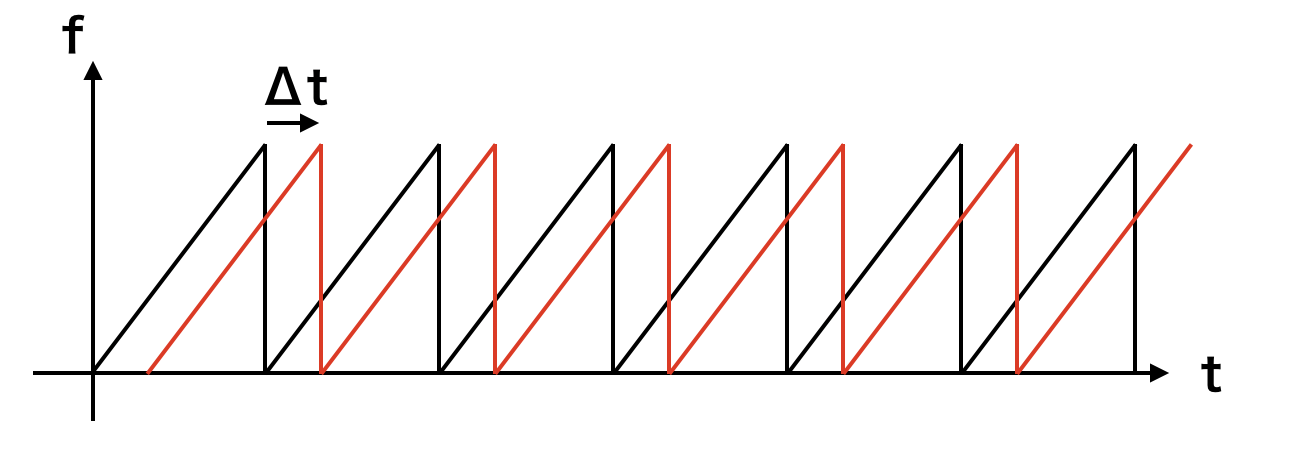
FCMのビート信号はこのようになります。FCMでは周波数が下降する変調がないので、ビート周波数は$f_u$のみです。
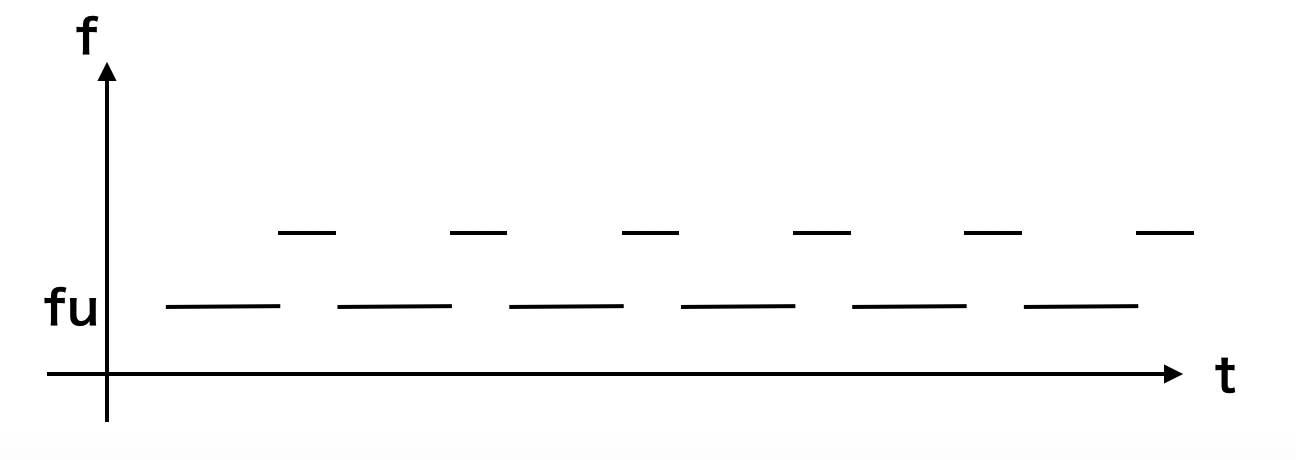
時間差$\Delta t$は
$$\Delta t=\cfrac{2R}{c}$$
で、ビート周波数$f_u$は
$$f_u=\cfrac{BW}{T}\Delta t$$
です。これより、
$$R=\cfrac{cT}{2BW}f_u$$
となります。これはビート周波数をFFTして求めます。
速度はFMCWとは違う計算で導きます。
上のグラフで$t=\Delta t$のときのビート信号の位相はこのようになります。
$$\psi_1=2\pi f_c\Delta t=\cfrac{2\pi R}{\lambda_c}$$
$t=T+\Delta t$では、 $vT$だけ物体が移動しているので、周波数変動はごく小さいですが、位相が変動します。この時の位相はこの通り、
$$\psi_2=\cfrac{2\pi (R+vT)}{\lambda_c}$$
したがって、速度による位相変動を読み取れば、物体の速度を検知できます。$\Delta \psi=\psi_2-\psi_1$はこのようになります。
$$\Delta \psi=\cfrac{2\pi vT}{\lambda_c}$$
$$v=\cfrac{\lambda_c\Delta \psi}{2\pi T}$$
正確には$t=\Delta t$のときと$t=T+\Delta t$では物体の距離が異なるので、周波数$f_u$が変化しますが、FCMの変調周期は鬼のように速いので、$f_u$の変化は無視できます。速度を示す位相差はビート信号を周波数方向にFFTすることで得られます。
まとめ
今日のまとめです。今日は距離、速度推定の原理を解説しました。検知に使う物理量は以下のとおりです。
| 距離 | 速度 | |
|---|---|---|
| パルス | 時間差 | 周波数 |
| FMCW | ビート周波数 | ビート周波数 |
| FCM | ビート周波数 | 位相差 |
- パルスはビート信号を使わないので、高周波クロックが必要ですが、距離精度に優れます。
- FMCWはビート周波数によって高周波クロックを必要としませんが、周波数のペアリングを行う必要があります。
- FCMはFMCWの原理をアレンジし、位相差で速度を検出するので、FFTを2回行うことで速度と距離を導けます。
次回はFCMを例にとって軽いシステムを組んでみます。