はじめに

ブラインド商法の欲しい景品を得るのに必要な試行回数を計算しよう。

結論から

全$N$種のガチャから$n$種の景品を引くまでの回数の期待値は

$$N \times \left( 1 + \frac{1}{2} + \cdots + \frac{1}{n} \right)$$

である。

理論

クーポンコレクター問題

全$N$種のブラインド商品から全種類を引くまでに必要な試行回数を求める問題は クーポンコレクター問題として知られています。同様の事例として、ちょっと前はコンプリートガチャなんかが社会問題になりましたね。ガチャの特定の種類をすべて収集すると別のアイテムがもらえるというシステムです。

ただ全種類ではなく、自分の推しが関連する商品だけ欲しいということもあるのではないでしょうか。今回はクーポンコレクター問題の派生系として、全$N$種のガチャから一部の$n$種を引くのに必要な回数の期待値を求めます。

式の導出

計算方法は以下のサイトを参考にしました。

まずガチャについての前提条件を定めます。

各景品が出る確率はすべて等しいとする。
ガチャを引く各回で景品が出る確率は変動しない。

すでに$k$種を引いた状態で、新たに1種類を引く確率変数を$X_k$とします。

求めたい期待値は
$$E[X_0 + X_1 + \cdots + X_{n-1}]$$
です。期待値の線形性からこの式は
$$E[X_0 + X_1 + \cdots + X_{n-1}] = \sum_{k=0}^{n-1} E[X_k]$$
となります。

次に$X_k = m$となる確率を求めます。これはつまり、すでに$k$種を引いた状態で$m-1$回まで目当てのものが引けず、$m$回目に引けるという場合です。すでに持っている$k$種と、狙っていない$N-n$種はいらないので
$$\left(\frac{k + (N-n)}{n}\right)^{m-1} \left(1 - \frac{1 - k + (N-n)}{N}\right)$$
となります。

期待値の定義から
$$E[X_k] = \sum_{m=1}^{\infty} m\left(\frac{k + (N-n)}{n}\right)^{m-1} \left(1 - \frac{1 - k + (N-n)}{N}\right)$$
となります。こちらに載っている方法を使うと、次のような計算結果になります。
$$E[X_k] = \frac{N}{n - k}$$

以上から、全$N$種のガチャから$n$種を引くのに必要な試行回数の期待値は

\begin{align}
E[X_0 + X_1 + \cdots + X_{n-1}] &= \sum_{k=0}^{n-1} \frac{N}{n - k} \\
&= N \times \left( 1 + \frac{1}{2} + \cdots + \frac{1}{n} \right)
\end{align}

となります。

$n=N$とすれば全種類を引く場合と同じになります。

さらに$n$が十分大きいとき
$$
1 + \frac{1}{2} + \cdots + \frac{1}{n} \simeq \log n
$$
という近似が成り立つので、
$$
E[X_0 + X_1 + \cdots + X_{n-1}] \simeq N \log n
$$
と近似することができます。

実例

全12種($N=12$)のガチャから目当ての4種($n=4$)を引くのに必要な回数の期待値は
$$\sum_{k=0}^{3}\frac{12}{4-k} = 25$$
と見積もれます。

ちなみに全12種類をコンプリートする場合は
$$\sum_{k=0}^{11}\frac{12}{4-k} \simeq 37.2385$$
です。

一部の種類を集めるだけでも、結構な試行回数が必要ですね。

シミュレーション

$N=12$、$n=4$の場合のシミュレーションを行ってみましょう。
目当ての景品が揃うまでガチャを引くようにプログラムを書き、試行回数をヒストグラムで表示します。
試しにサンプル数50000で回してみます。

import random
import matplotlib.pyplot as plt
import seaborn as sns

# ガチャ
def gacha(N):
  return random.randint(1, N)

samples = 50000
N = 12
n = 4
wish_list=set(range(1, n+1))
trial_times = []
for i in range(samples):
  got_list = set()
  t = 0
  while(not(wish_list <= got_list)):
    got_list.add(gacha(N))
    t += 1
  trial_times.append(t)

# Calculate the histogram of trial_times
sns.histplot(trial_times, stat="count", discrete=True)
plt.xlabel("Number of trials")
plt.ylabel("Frequency")
plt.title("Histogram of trial_times")
plt.show()

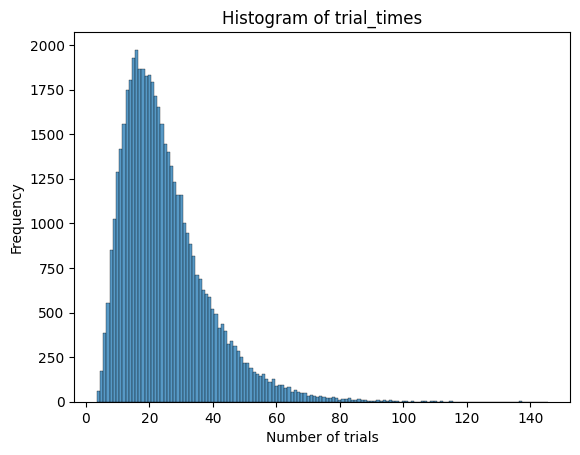
X軸が試行回数、Y軸がその試行回数で目当ての景品を得られたサンプル数です。

確実に引くには？

上の図を見て分かる通り、期待値を下回るサンプルもありますが、期待値を超えたサンプルも結構あります。
このガチャは天井がないので、運が悪いといくらでも試行回数が増えてしまいます。

じゃあ実際どのくらいガチャを引けばほぼ確実に目当ての景品が手に入るのでしょうか。

ブールの不等式を使って見積もってみます。

ガチャを期待値の2倍の回数引いても$k$番目の種類が引けない事象$A_k$が起こる確率$P(A_k)$は次のように求められます。
$$
P(A_k) = \left( \frac{N - 1}{N} \right)^{2 \times N(1 + 1/2 + \cdots 1/n)}
$$
目当ての景品が手に入らない確率は
$$
P(A_1 \cup \cdots \cup A_n)
$$
なので、ブールの不等式と$P(A_k)$の式から
$$
P(A_1 \cup \cdots \cup A_n) \leq \sum_{k=1}^{n} P(A_k) = nP(A_1)
$$
が言えます。
さらに

\begin{align}
P(A_1) &= \left( \frac{N - 1}{N} \right)^{2 \times N(1 + 1/2 + \cdots 1/n)} \\
&= \left[ \frac{1}{(1 - 1/N)^{-N}} \right]^{2 \times (1 + 1/2 + \cdots 1/n)}\\
& \leq \left( \frac{1}{e} \right)^{2 \times (1 + 1/2 + \cdots 1/n)}
\end{align}

と求められる。

具体的に$N=12$、$n=4$の場合を求めてみると

\begin{align}
nP(A_1) = 4 \times \left( \frac{1}{e} \right)^{2 \times (1 + 1/2 + 1/3+  1/4)} \simeq 0.06
\end{align}

なので、ガチャを期待値の2倍の回数引いても揃えられない人は6%以下だとわかります。
逆に言えば94%以上の人たちは目当ての景品を揃えられそうです。

最後に

自引きで揃えるのはやっぱり大変。
ぼっちにはトレード文化つらい。