統計検定「データサイエンス基礎」の学習あと

先日、「統計検定 データサイエンス基礎」を受けて合格できたので、必要な知識をまとめてみる。

（本記事で使用している主なデータ）
kaggleのTitanicデータ
※実際に取得するには、kaggleの登録が必要。

「統計検定 データサイエンス検定」について

試験内容や難易度、所感

概要や出題範囲はこちら。
https://www.toukei-kentei.jp/about/grade11/

この試験は、具体的なデータセットを用いたExcelでの実技が伴う。

勉強＆受験してみて、
理論もある程度おさえながらそれを表現するためのExcel上でのデータハンドリングスキルも学ぶことができるため、実践的で良い資格だと思った。

資格を取るためだけの勉強ではなく、実務でもすぐに使えるExcelでのデータ処理が身につく点がとても良い。実際、自分は基礎統計や検定、簡単な回帰分析なんかは、今後はExcelでやってしまおうと思うようになった。

難易度は、経験者にとってはそこまで高くはないが、初学者にとってはそこそこ。
理論部分については「統計検定3級〜2級（一部）」の理解が必要。
統計検定2級保有者であれば、理論部分で新しく学ぶことはさほどなく、Excelでの実装方法の学習がメインになる。

学習の進め方

本試験は、参考書や過去問がなくサンプル問題もほとんどないため（2021年11月時点）、対策がなかなか難しい。

学習の進め方としては、出題範囲に書かれている手法の理論を学び、Excelの関数や表現式を調べ、実際に手を動かしながら（多少行き来しつつ）、理解を深めていくのが良いと思う。

理論に力を入れすぎるよりも、手を動かしておくのが重要（たぶん）。
適当なオープンデータを準備して、覚えたことをどんどん実践してみるのが良いと思われる。

まず始めに、公式ページにあるサンプル問題をやってみて雰囲気を見ておくとよい。

学習時間

一概には言えないが、

• 統計検定2級（3級でも良いかな？）以上の保有者であれば、15〜20時間くらい
• 統計検定初挑戦であれば、40〜60時間くらい

かな？ （根拠レス）

自分が、前者のケースで20時間程度は勉強したかなという感じ。

すでに理論的な部分を抑えている人は、ざっと復習＋Excelでの練習くらいで良いかなと。
さらに、もともとExcelでの統計処理にも慣れている人は、ほとんど勉強不要かと思われる。

理論的な部分から学習が必要な人は、ある程度時間が必要になるかなと。

学習あと

各種手法、理論について

主題範囲の「項目（学習しておくべき用語）」について、用語の意味や理論的な部分、手法の用途などを一通り学ぶ。

統計検定3級・2級の教科書やWebサイトなどを参考にする。
とくに、自分の場合は下記サイトにお世話になった。概ね本試験の範囲を網羅している上に、とても分かりやすい。
統計学の時間：https://bellcurve.jp/statistics/course/

Excelの事前準備と小技

データ分析ツールの有効化（事前準備）

あらかじめ「データ分析」ツールを有効にしておく。（方法はググる）

※参考：「データの分析」
「データ分析」とは別に、ホームに「データの分析」がある。
実行すると、いくつかの分析の「アイデア」が自動で実行され、データに対する洞察を得る事ができる。（試験から多少逸れるが）本機能は結構面白く、実践においてデータに初めて向き合う時には良いかもしれない。

Excel小技（覚えておくと試験がスムーズかも）

問題数に対して試験時間はわりと短いため、Excel操作をスムーズにできるときっと有利。
ここでは、そんな効率化に使える小技を挙げてみる。

数式内のセル表記を絶対参照にする（「$」を付与する）

「A1:A15」→ 「$A$1:$A$15」というように、「$」を付与する。

セル表記上で「F4」

※カーソルの位置や選択状態により、$を付与する範囲を制御できる。
例えば、A1:A15を範囲選択していれば「$A$1:$A$15」となり、A1の”1"の後ろにカーソルがあれば「$A$1:A14 」というようにA1のみが対象となる。

下の列へ連続コピー

セル内へ関数を入力したら、そのセルの右下の黒い■をダブルクリックすることで後続のセルへ内容がコピーされる。

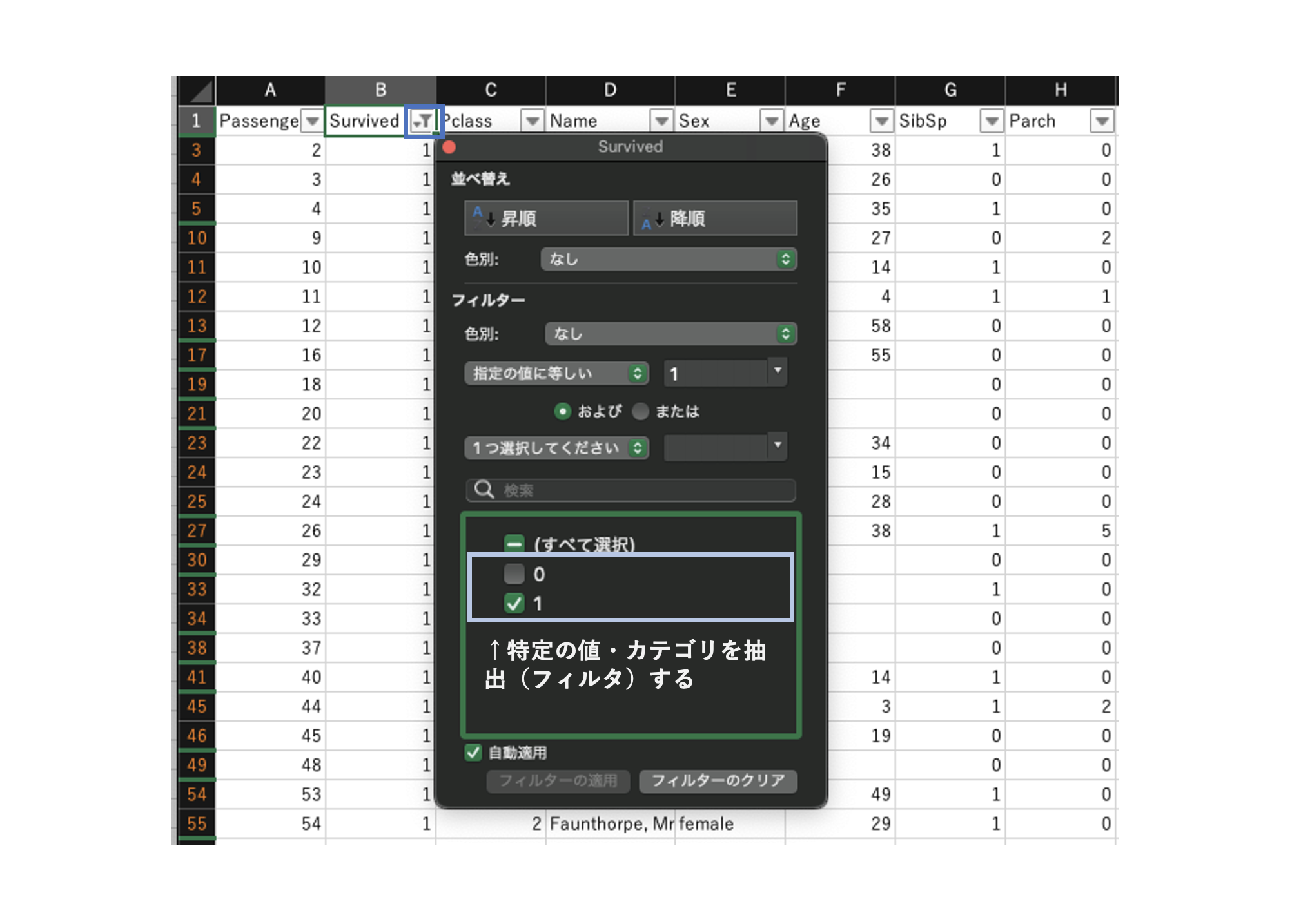
フィルターで対象行を絞る

行列に整形されたデータにおいて、各列にフィルターを設定して特定のカテゴリや条件で行を絞ることができる。

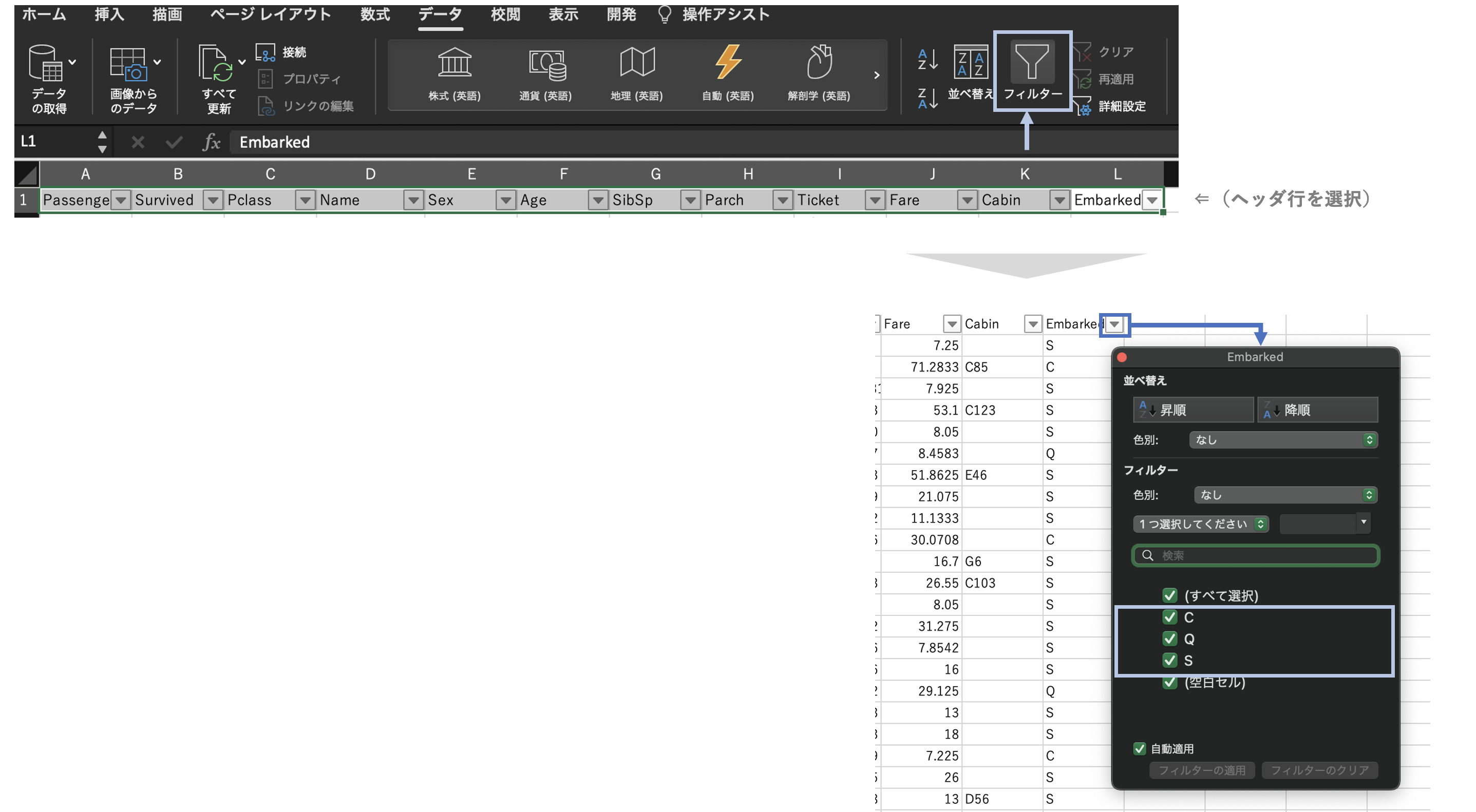
ヘッダ行を選択して、データ＞フィルター
で、フィルターを設定したら、ヘッダの「▼」よりフィルタリングする

少数点表示桁数を変更

ホーム＞点表示桁上げ（下げ）

行を追加する、削除する

# カーソル位置に新規行を追加
「ctrl」 + 「+」

# カーソル位置の行を削除
「ctrl」 + 「-」

（番外）ウィンドウの切り替え

試験環境はWindowsのため、「Alt」+「Tab」で開いているウィンドウを切り替えられる。
これに慣れていれば、回答画面とExcelの切り替えがスムーズにできるので試験時間のロスを減らせる。

各学習項目とExcelでの実装方法

データベース・マネジメント

データのソート（並べ替え）

特定の列（1列、または複数列）の値を用いて昇順や降順に並べ替える。

（ある1列の値でソートする場合）
ヘッダ行にフィルターを設定し、ソートのキーとなる列でフィルター＞並べ替えを実行する。

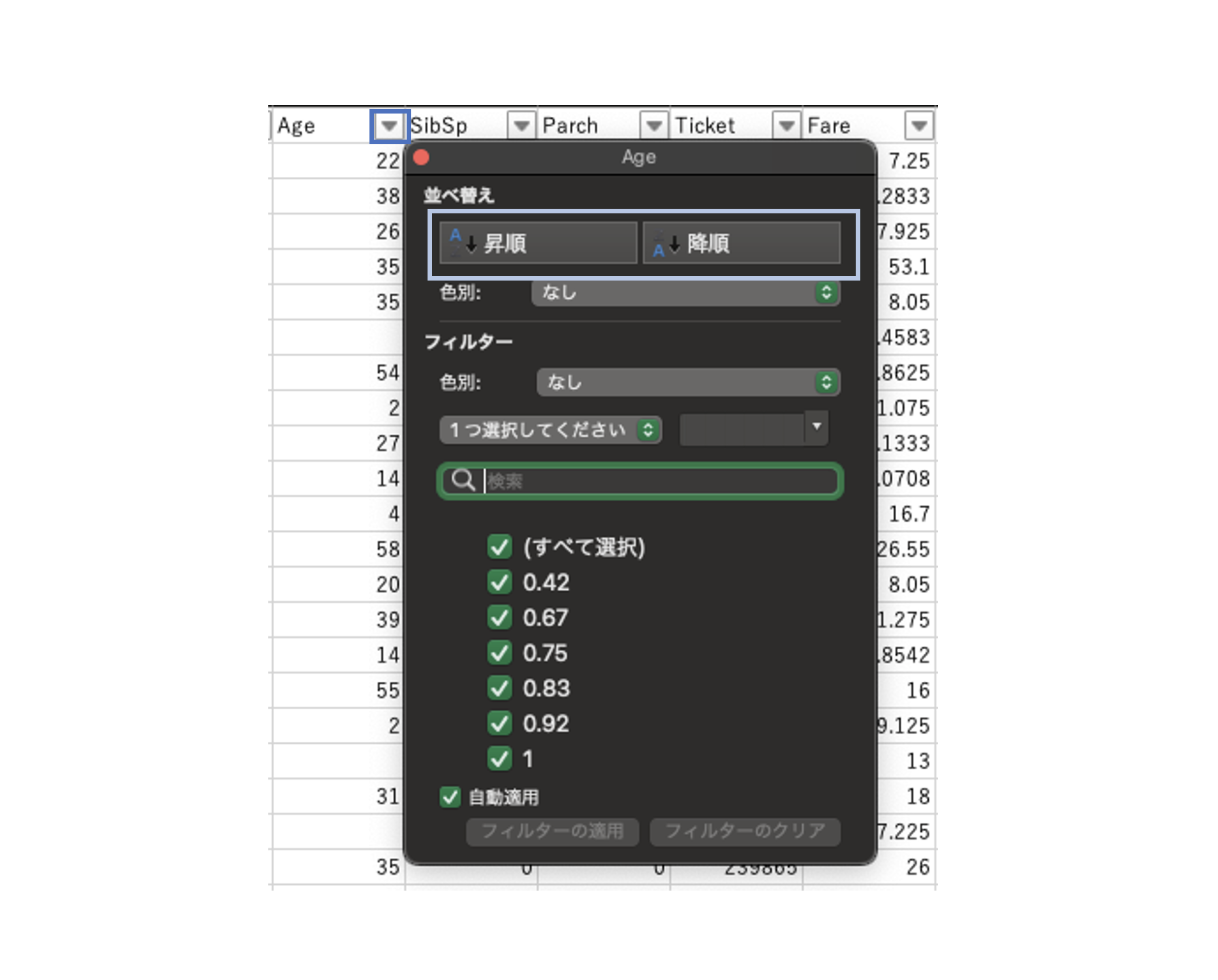
（複数列の値でソートする場合）
ホーム＞ユーザー設定の並べ替え...で設定することで、各列の優先度順に応じて並べ替えが実行される。

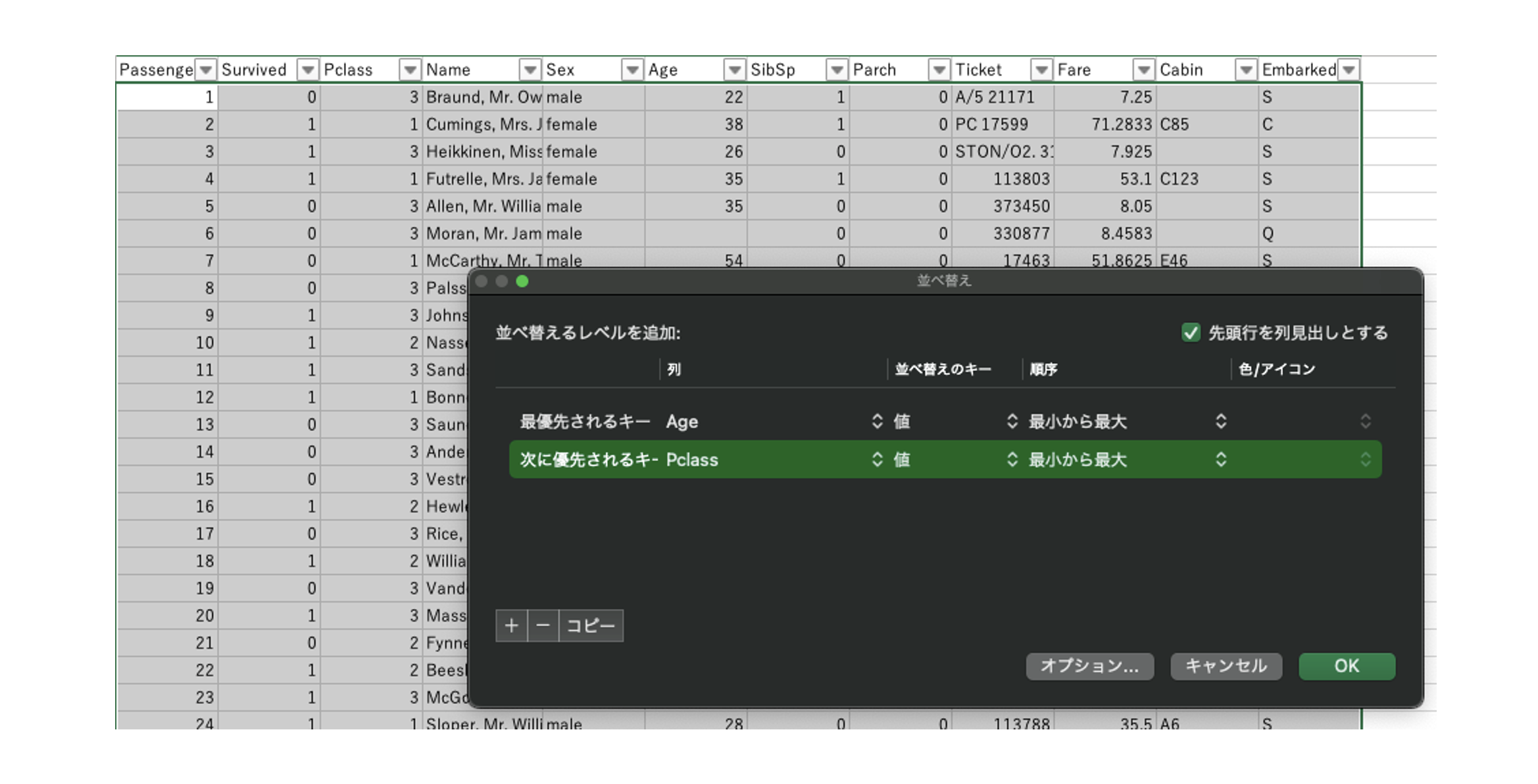
上の例では、Ageで並べ替えた後に、Ageが同一の行はPclassで並べ替えられる。

欠損値の数を確認

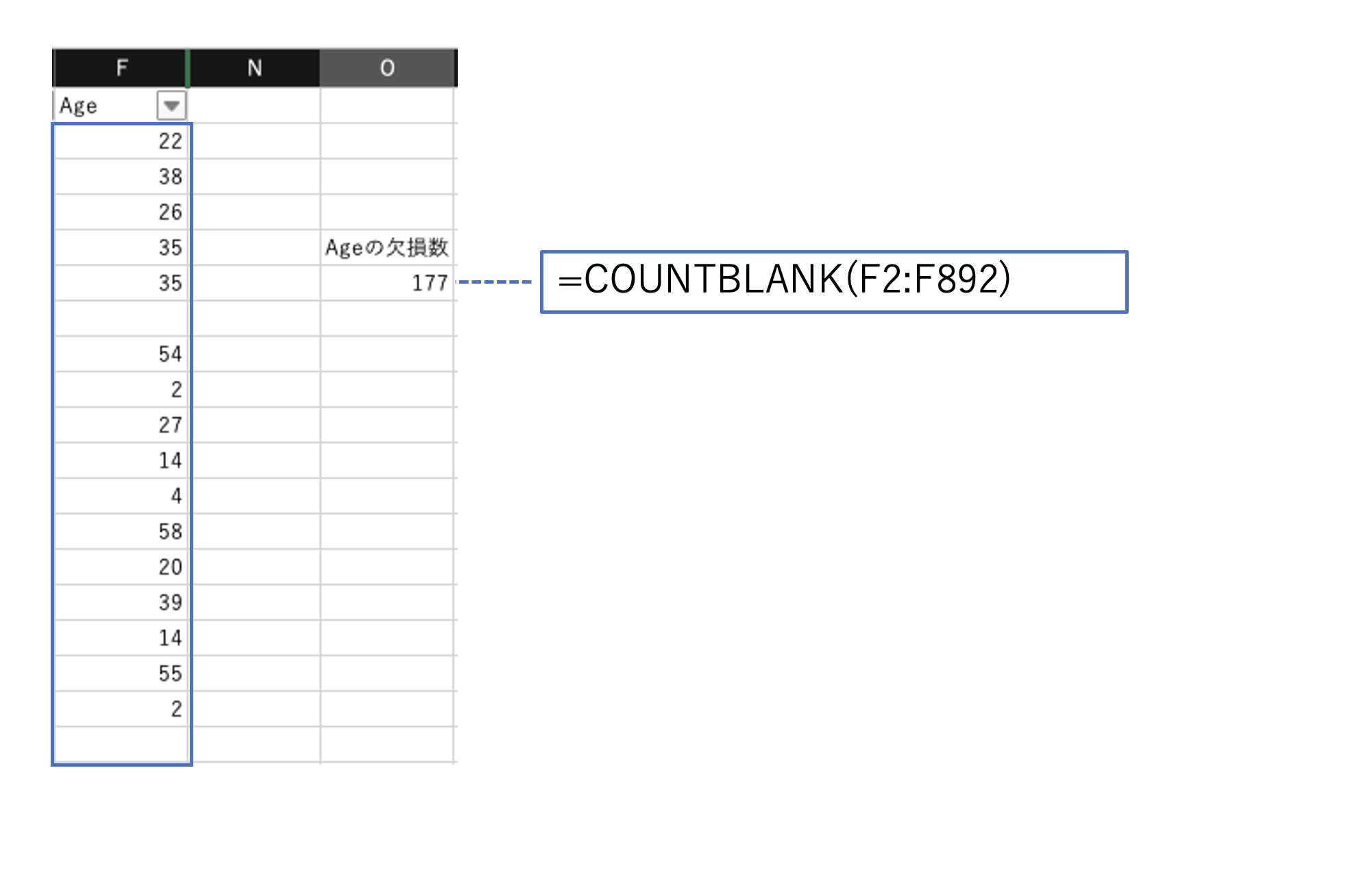
（数式で、欠損数の確認）

COUNTBLANK(対象配列)

（お手軽に、欠損数の確認）
対象列を選択してステータスバーを確認する。

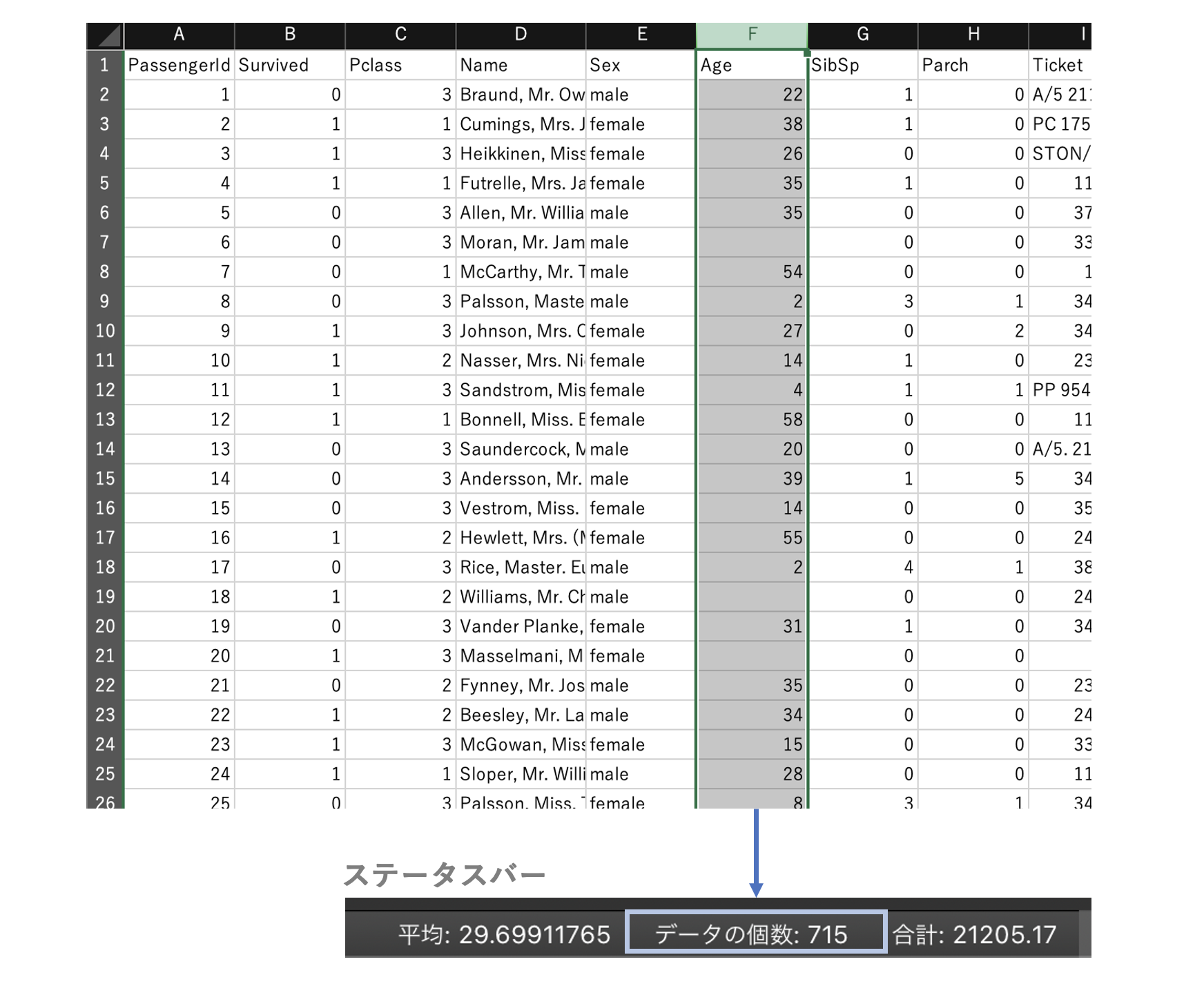
「データの個数」に欠損していない値の数が表示される。
なお、欠損値の数は、全レコード数から「データの個数+1」を引くことで求められる。
（データの個数にはヘッダ行（1行目）も含まれるためそれも引いている。）

実践的には、厳密な欠損の数を把握するというよりも、ざっと欠損がどの程度あるか見るのに使える。

欠損値を補完

IF(ISBLANK(対象配列), 補完値)

上の例では、（欠損していないデータの）平均値で補完。

データの結合

Power Queryを使うことで可能。
ただし、試験では問われる可能性が低い（かな？）と思うので割愛。

なお実践的には、VLOOKUP関数で必要なデータを取りしてきて結合的な操作をすることが多いと思う。
（ちなみに、VLOOKUPは左外部結合）

結合の種類（内部／外部、左／右など）は抑えておく。

データ形式（ロングフォーマット⇔ワイドフォーマット）

データ結合同様、Power Queryを使うことで可能。
こちらも、試験では問われる可能性が低い（かな？）と思うので割愛。

なお実践的には、ピボットテーブルで、必要な軸をクロスした表現した形（ワイドフォーマット）を扱うことが多いと思う。

ロングフォーマットとワイドフォーマットがどんな「形」か抑えておく。

乱数

（関数による乱数発生）

#0～1の実数をランダムに得る。
RAND()

#指定した範囲の整数をランダムに得る。
RANDBETWEEN(最小値, 最大値)

#ランダムな数値を配列で得る。
RANDARRAY(行数, 列数, 最小値, 最大値, 整数)

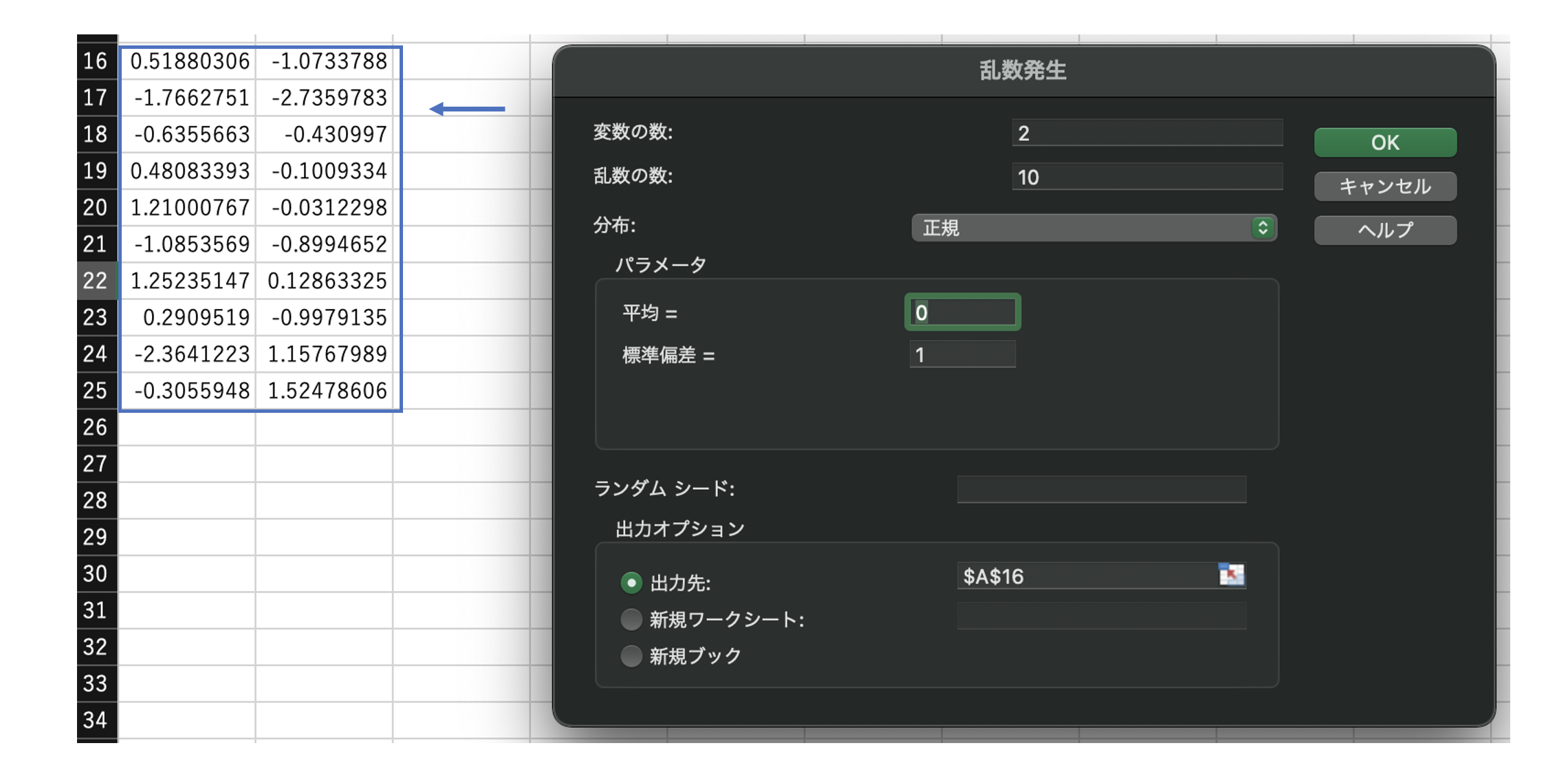
（データ分析ツールによる乱数発生）
データ ＞ データ分析 ＞ 乱数発生で乱数を生成できる。
乱数生成元の分布を、一様、正規、ベルヌーイなど複数から選択できる。

（例：正規分布に従う乱数の生成）

データ抽出（ランダムサンプリング）

Excelで明示的なランダムサンプリング関数等はないので割愛。
（RAND関数を利用した方法等は一応ある。）

下記あたりを抑えておく。

• 母集団からサンプリングしたデータは、標本（サンプル）と呼ばれる
• サンプリングはランダム（無作為）で行われることが重要である

データマネジメント

質的データと量的データ （データ尺度）

※これ自体に対するExcel操作は特にない。
それぞれのデータ尺度の違い、および各データで適用可能な計算や分析手法を抑えておくと良いかと思う。

• 名義尺度
  可能な計算：なし
  適用できる手法：各ケースの数、計数（count）、頻度（frequency）、最頻値、連関計数

• 順序尺度
  可能な計算：大小比較
  適用できる手法：中央値、パーセンタイル

• 間隔尺度
  可能な計算：大小比較、和（＋）、差（−）
  適用できる手法：平均値、標準偏差、順位相関係数、積率相関係数（いわゆる相関係数のこと）

• 比例尺度
  可能な計算：大小比較、和（＋）、差（−）、積（×）、商（÷）
  適用できる手法：変動係数

※参考
データの種類 (質的データ、量的データ)：https://www.codereading.com/statistics/level-of-measurement.html
変数の分類：https://bellcurve.jp/statistics/blog/14248.html

層別と水準（レベル）化

（層や水準の確認）
フィルターのカテゴリリストで確認する。

実践的には、層別の的確さが重要。向き合っている問題に対し、「さらに絞込んでいくにはどのような軸がよいか？」を感度良く見つけていくことが求められる。

（水準化の実装）
下記関数により、元データの値を判定し水準（大きさやレベルを表す値）に置き換える。

IF(式, 値1、値2）
SWITCH(式, 値1, 結果1, 値2, 結果2, …)

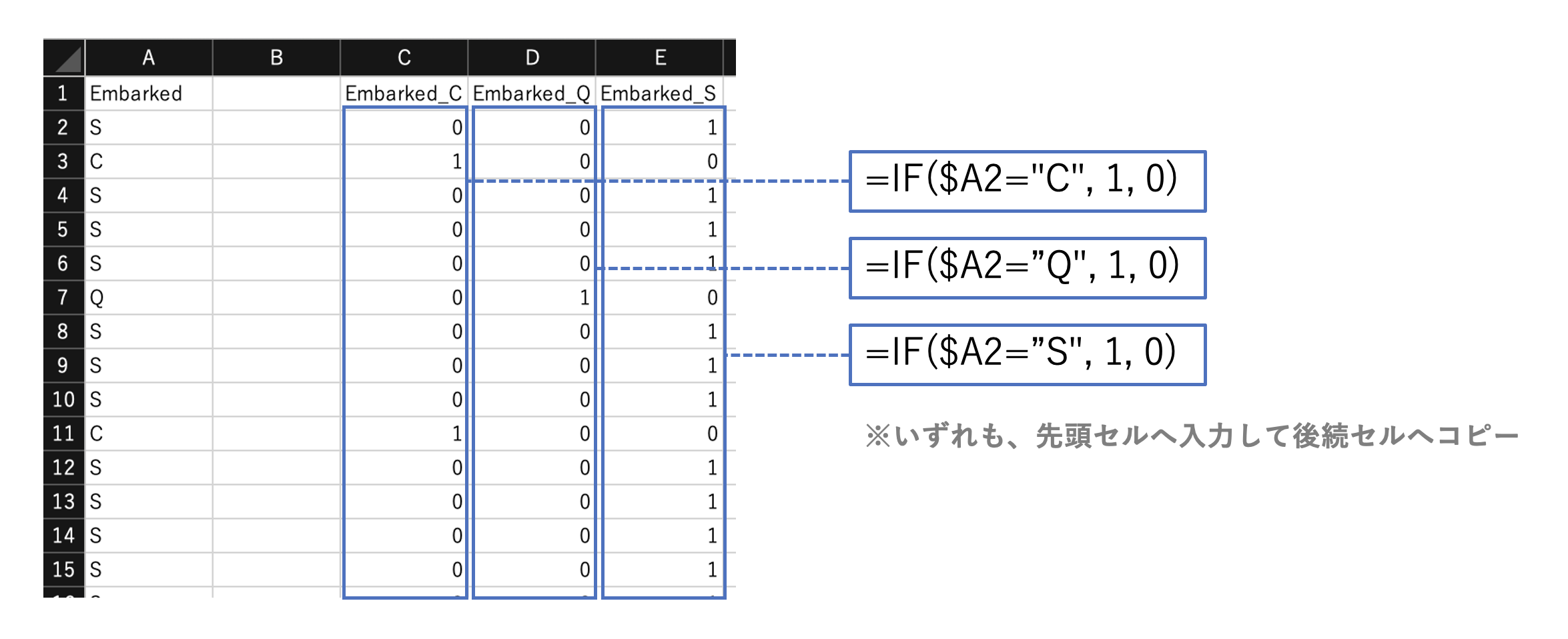
同じ要領で、回帰分析等で必要な1-0表現（ダミー変数化）も実装できる。

変数変換

変数変換は、関数で元の数値を変換すること。
具体的に、何を指しているか分からなかったので、試験で出そうな下記の関数を確認しておく。

# 累乗 Xのa乗
X^a

# 平方根 Xの平方根（どちらも同じ結果）
SQRT(X)
X^0.5 

# 対数 aを底としたXの対数を求める（底は省略すると10）
LOG(X, a)

Z変換（標準化）

データの平均値からの偏差を標準偏差で割ったもの。

STANDARDIZE（X, 平均, 標準偏差）

（例：平均60点、標準偏差20点のテストにおけるZ変換値）

偏差値

Z変換した値に10を掛けて50を加えたもの。

STANDARDIZE（X, 平均, 標準偏差）* 10 + 50

（例：平均60点、標準偏差20点のテストにおける偏差値）
上記のZ変換値を用いて

• 40点の場合、 -1*10+50 = 40
• 60点の場合、 0*10+50 = 50
• 80点の場合、 +1*10+50 = 60

データの可視化

各種グラフの形状と特徴

それぞれのグラフの形状、特徴、Excelでの作り方を確認しておく。
（今までに作成経験のないグラフは一度作ってみるとよいかも）

挿入 ＞円グラフ、棒グラフ、折れ線グラフ、帯グラフ、ツリーマップ、パレート図、ヒストグラム、箱ひげ図

とくに、試験本番でスムーズにグラフを作成できるように、各グラフメ作成のニュー位置は把握しておくとよいかも。
※各グラフはほとんどが直感的に作れるため、ここで作り方については割愛。

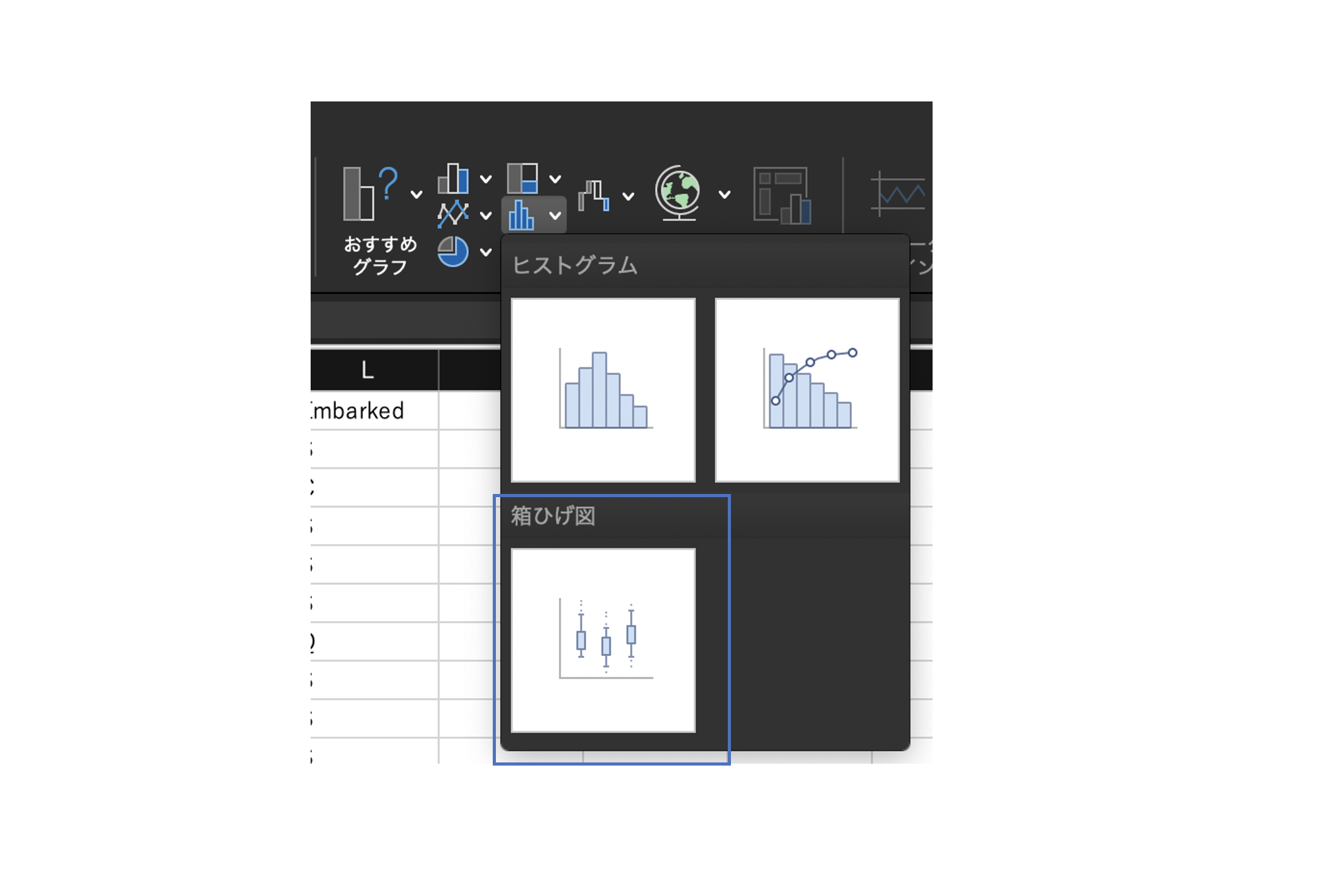
※参考：箱ひげ図のメニュー位置
個人的に、箱ひげ図の位置に迷うことがあるので載せておく。
「ヒストグラム」の下にある。ちなみにパレート図もこのグループにある。

1変量の質的データの分析

（1変量）構成割合、累積度数の作成

（ピボットテーブルでの作成）
対象の変数を含めたピボットテーブルで作成する。
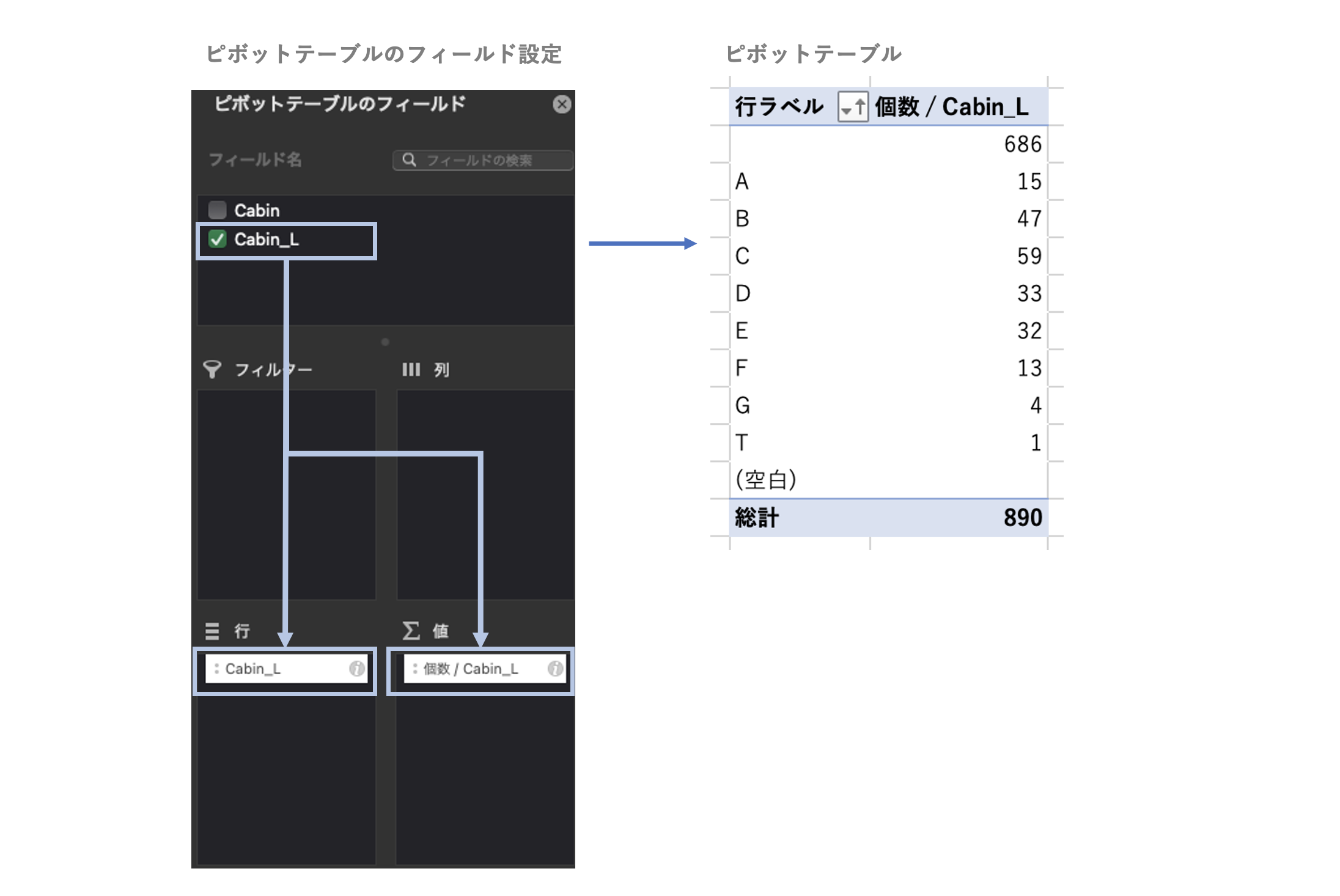
※ここでは、Titanicデータの「Cabin」列の各値の頭文字をとった「Cabin_L」列を用いた。

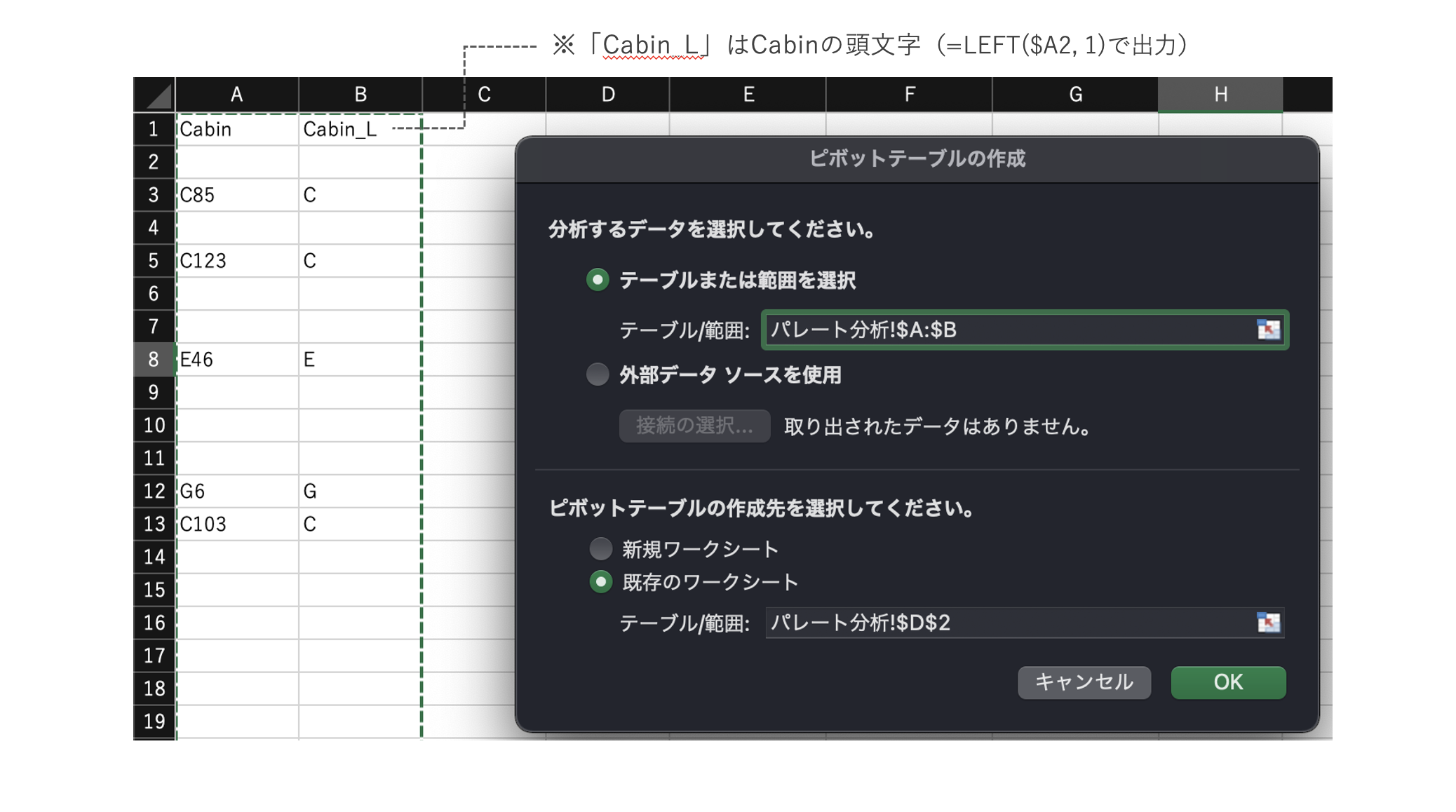
下記のピボットテーブルを設定して、Cabin_Lのカテゴリ毎のデータ数（カウント）を表示する。

• 「行」：Cabin_L
• 「値」：Cabin_L - 「個数」
  

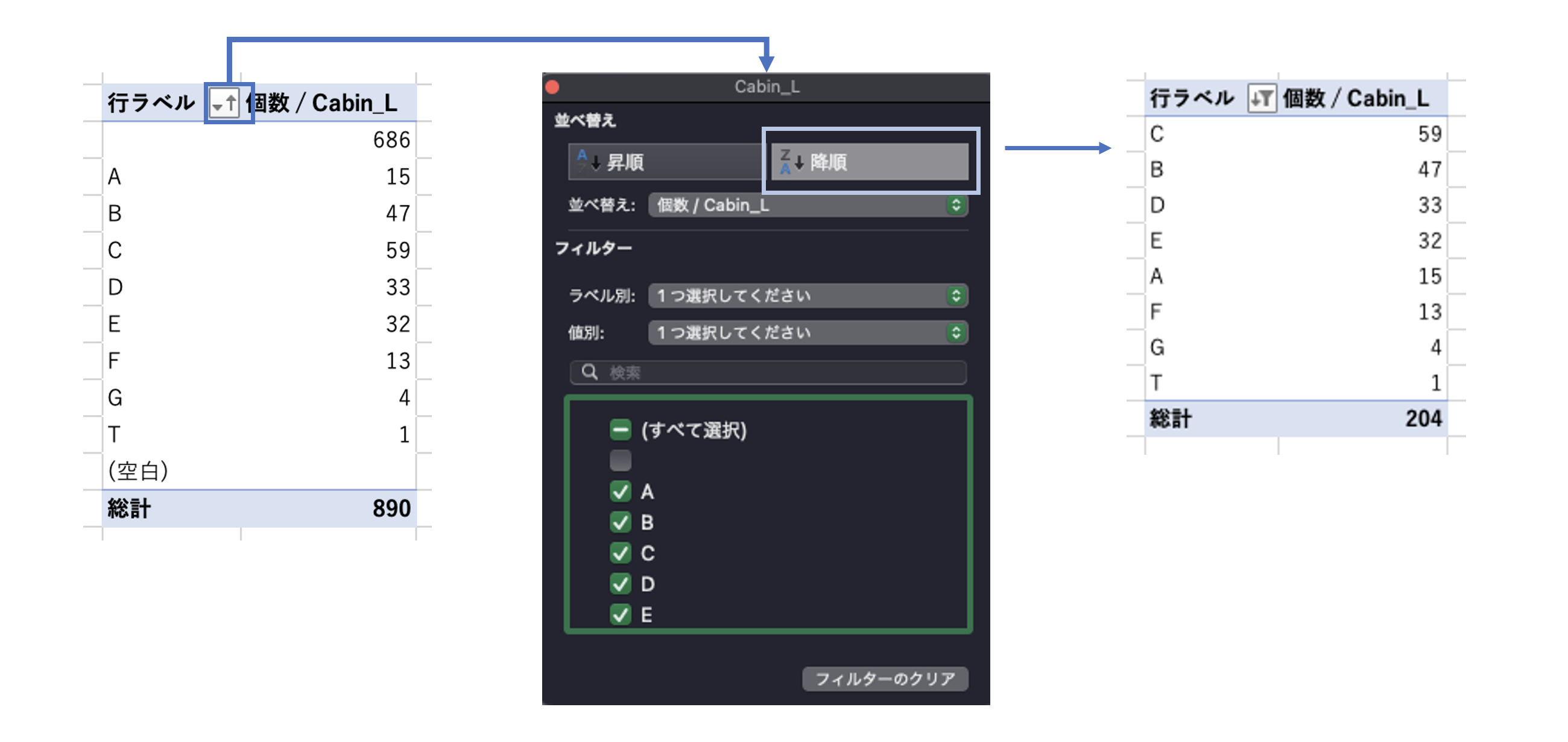
Cabin_Lの「個数」の降順でソートする。
（累積度数を求める上で、データは値の大きい順に並んでいる必要がある。）
※あわせて、フィルター機能で空文字も除外。

構成割合（カテゴリ別のデータ数÷総データ数）、累積度数（構成割合の累積）を求める。
※参考：ピボットテーブル自体は、まま複雑な数式になっているためここまで作成したデータをどこかへ「値コピー」してから実装したほうが分かりやすい。

※ピボットテーブル上で、次のようなピボットテーブルフィールドを作成することでも実現可能。

「構成割合」

• 集計の方法 ＝ 個数
• 計算の種類 = 列集計に対する比率

「累積度数」

• 集計の方法 ＝ 個数
• 計算の種類 = 比率の累計
• 基準フィールド ＝ Cabin_L

パレート図（表）の作成

データ数を棒グラフ、累積度数を折れ線グラフ（2軸目）とした複合グラフを作成する。

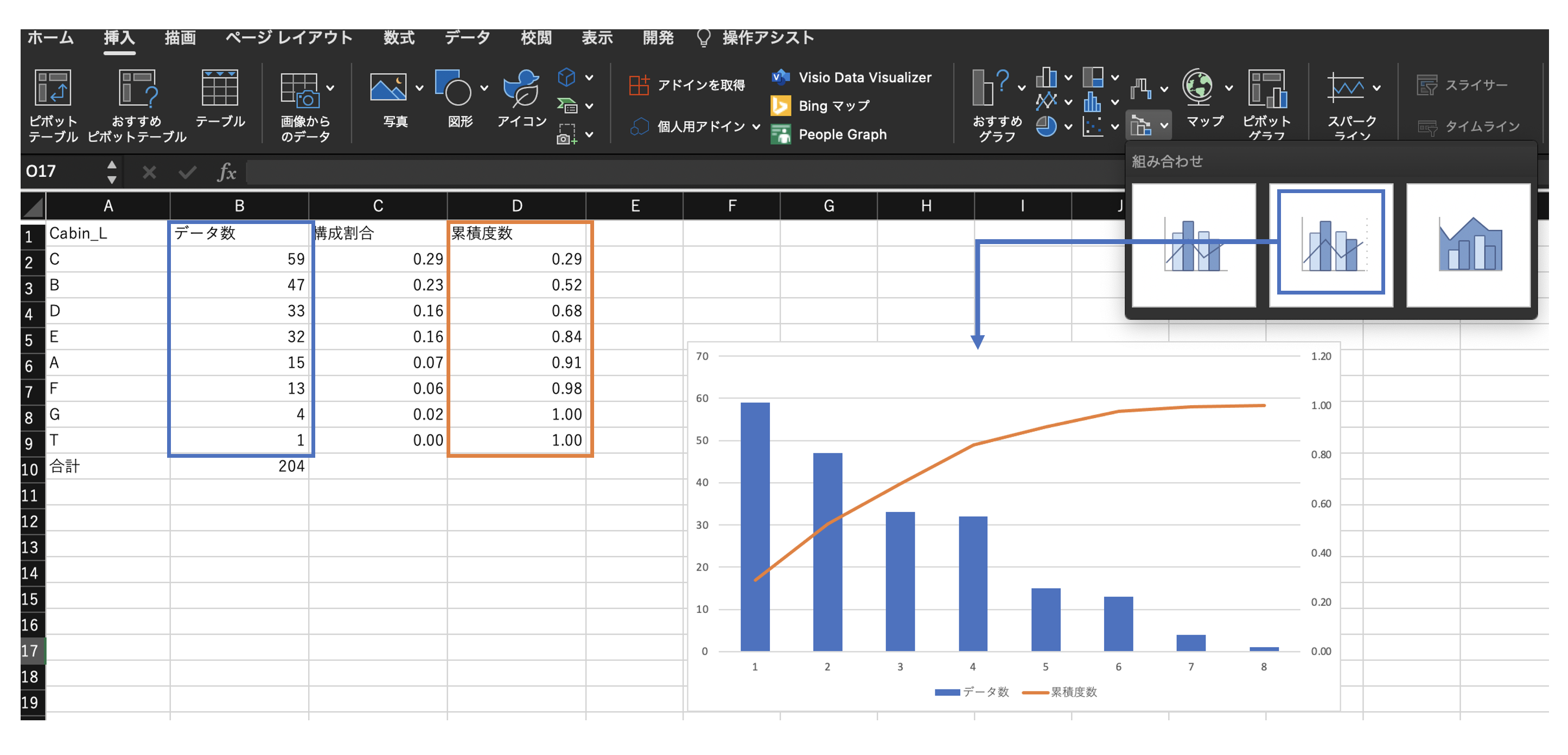
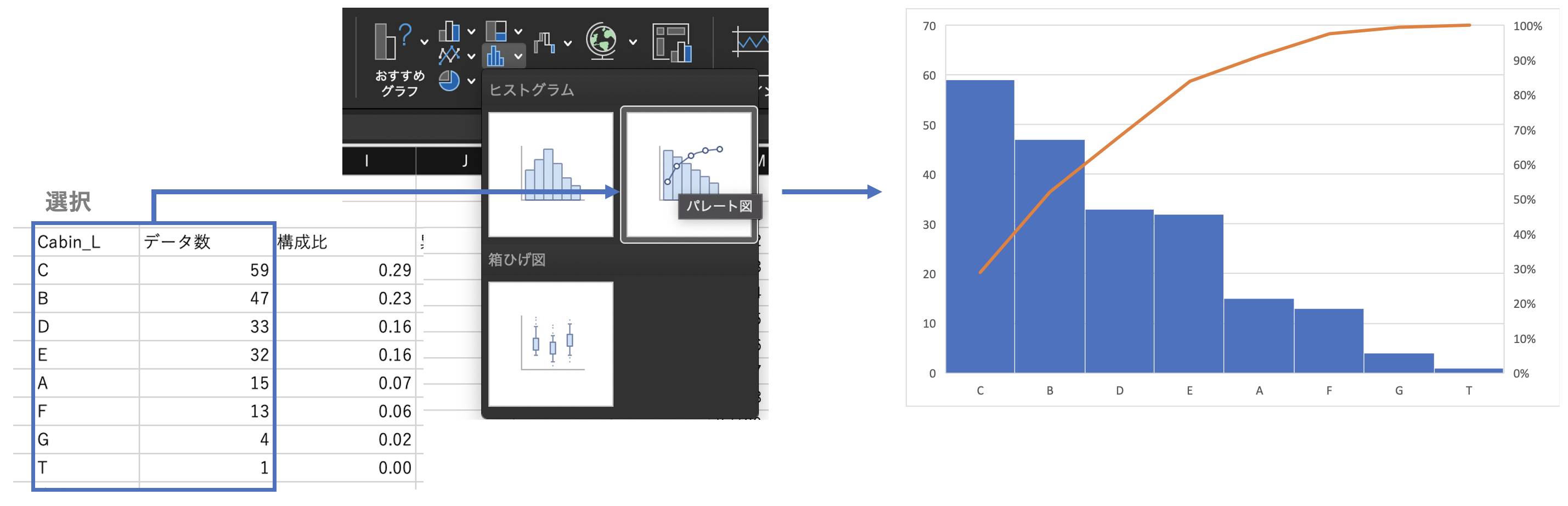
挿入＞パレート図により、各カテゴリとデータ数の表を指定するのみでパレート図を作成することも可能。

2変量以上の質的データの分析

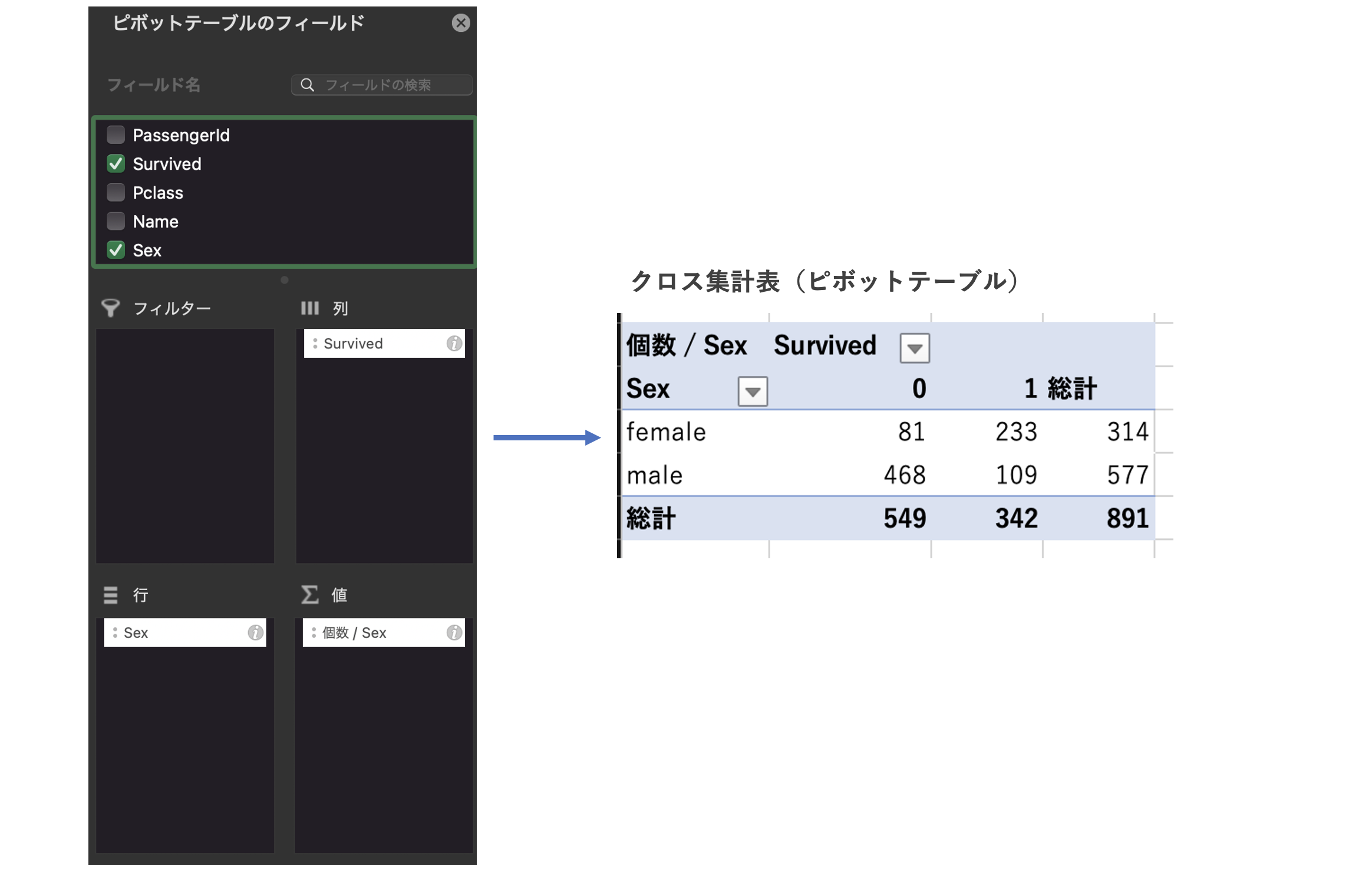
クロス集計の作成

対象の変数を含めたピボットテーブルで作成する。
※ここでは、Titanicデータの「Sex」×「Survived」のクロス集計表を作成した。

行比率、セル比率の算出

ピボットテーブル フィールドで作成する。
（「値」-「Sex」で右クリック「フィールドの設定」）

※クロス集計内の絶対値をみるよりも、行や列などの比率（%）をみることでカテゴリ間の差異の度合いを理解しやすいケースがある。

期待度数の算出

上記クロス集計表の期待度数を求める。
期待度数は「Sexに関係なくSurvivedが均等に別れた場合の値」を指す。

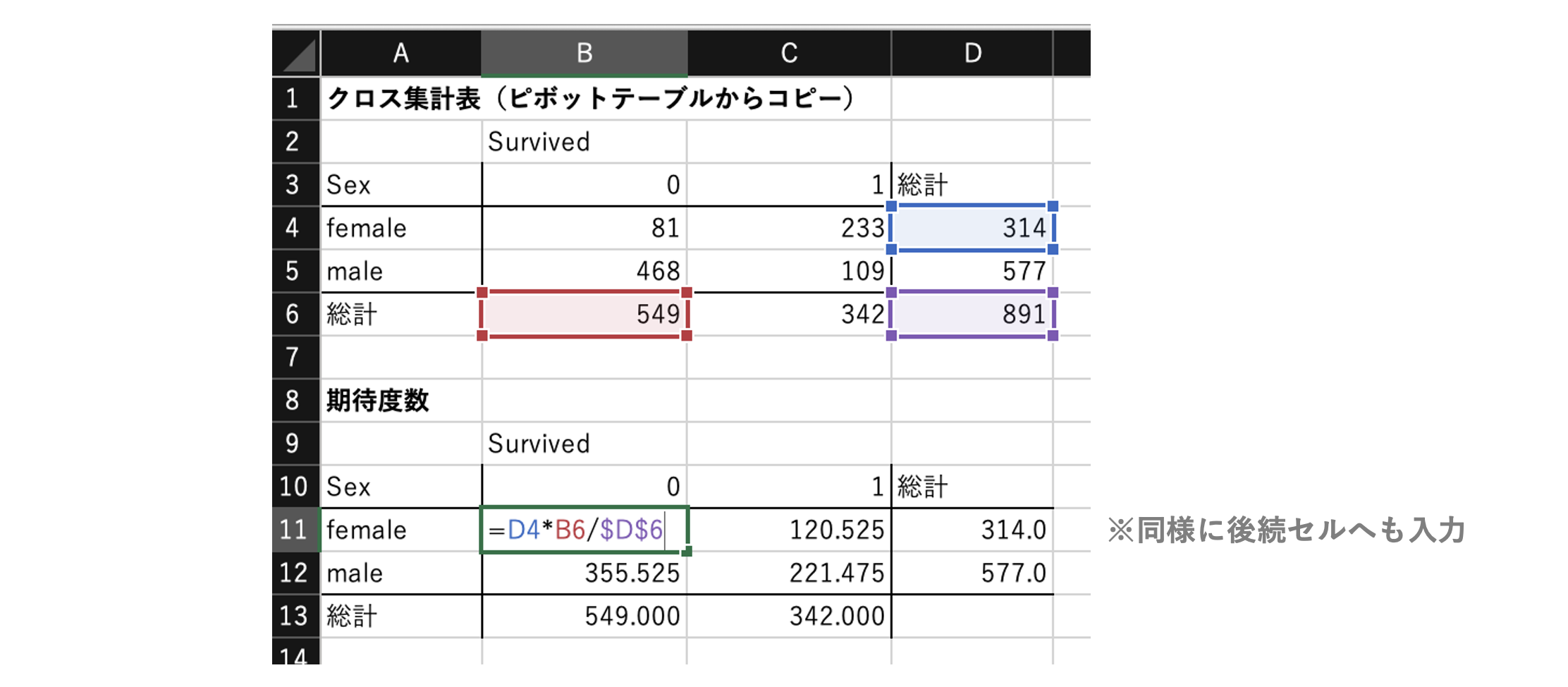
※クロス集計表をどこかへ「値コピー」して計算すると実装しやすい。

※参考
独立性の検定：https://bellcurve.jp/statistics/course/9496.html

• 「3. 適切な検定統計量を決める - ①理論値を算出する」

カイ２乗統計量の算出

上記クロス集計表の実測値と期待値の「へだたり度」を計算する。

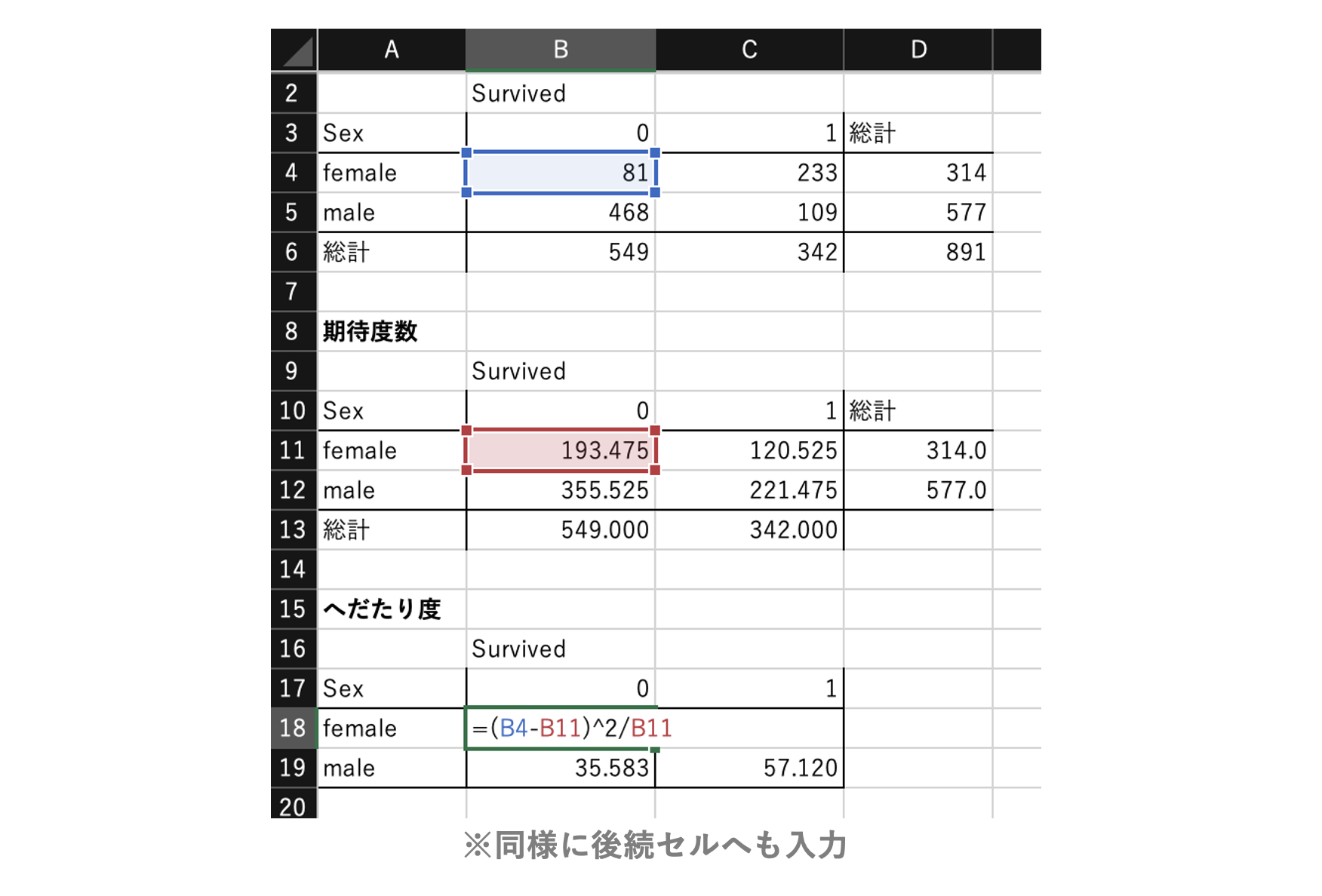
カイ2乗統計量は、へだたり度の合計。
実測値と期待値が完全に一致していれば0となり、一致性が低いと大きくなる。

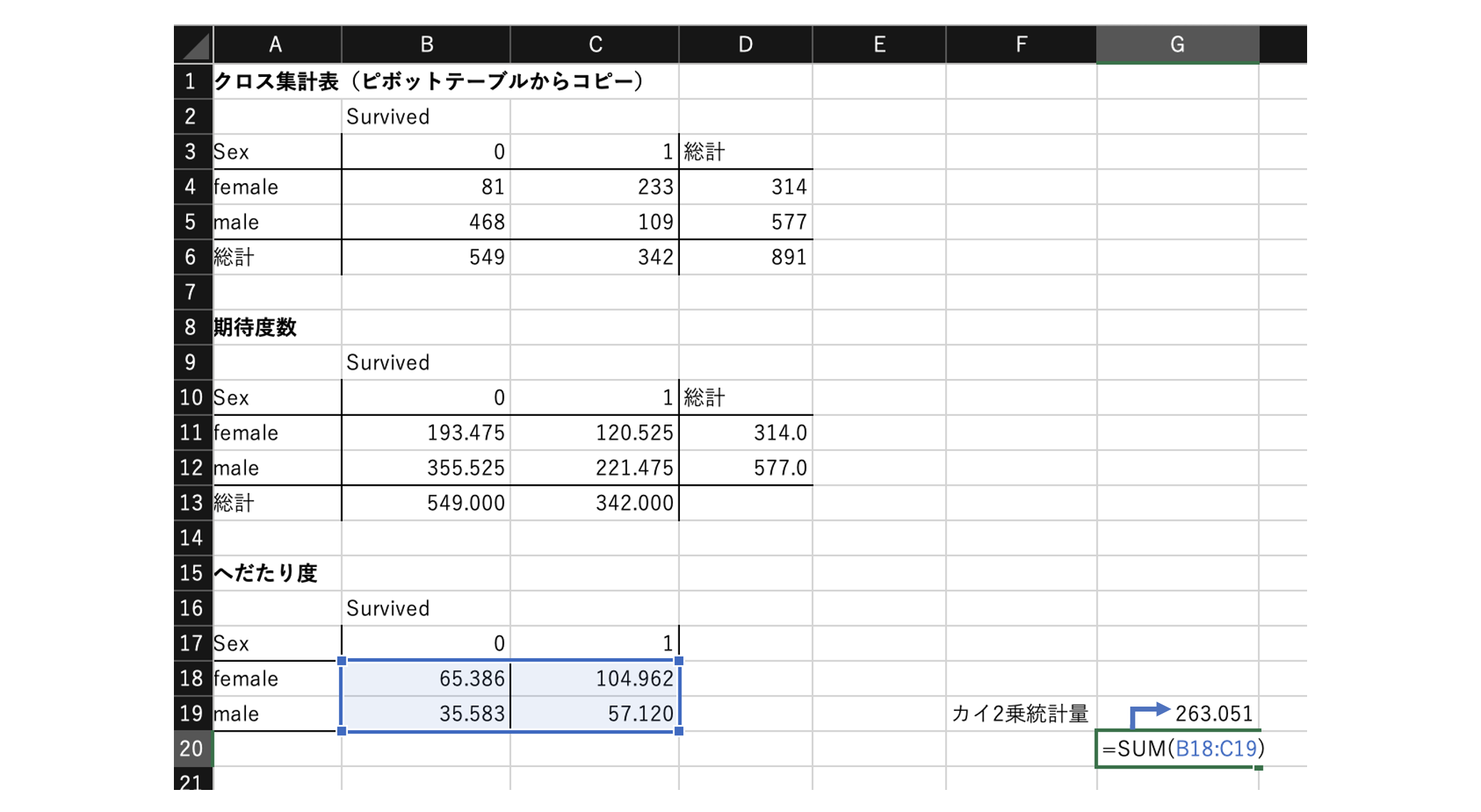
※カイ2乗統計量が大きいほど「クロスさせたカテゴリ×カテゴリの間には関連性がありそうだ」と判断できる。
（それを確率的に判断するのがカイ２乗検定 = CHISQ.TEST関数。後ろの章で出てくる。）

※参考
独立性の検定：https://bellcurve.jp/statistics/course/9496.html

• 「3. 適切な検定統計量を決める - ②〜③」

連関係数の算出

連関係数自体は、クロス集計表における行要素と列要素の連関の度合いを表す係数の総称で、クラメールやファイ係数、ユールなど様々ある。
試験としてはどの辺までの知識が問われるのかは不明。まずは、連関係数の目的等の概要を抑えておく。

ここでは、上記で求めたカイ２乗統計量を用いて「クラメールの連関係数」を求める。
※クラメールのV値は、0〜1の値をとり、1に近いほど関連が強い。

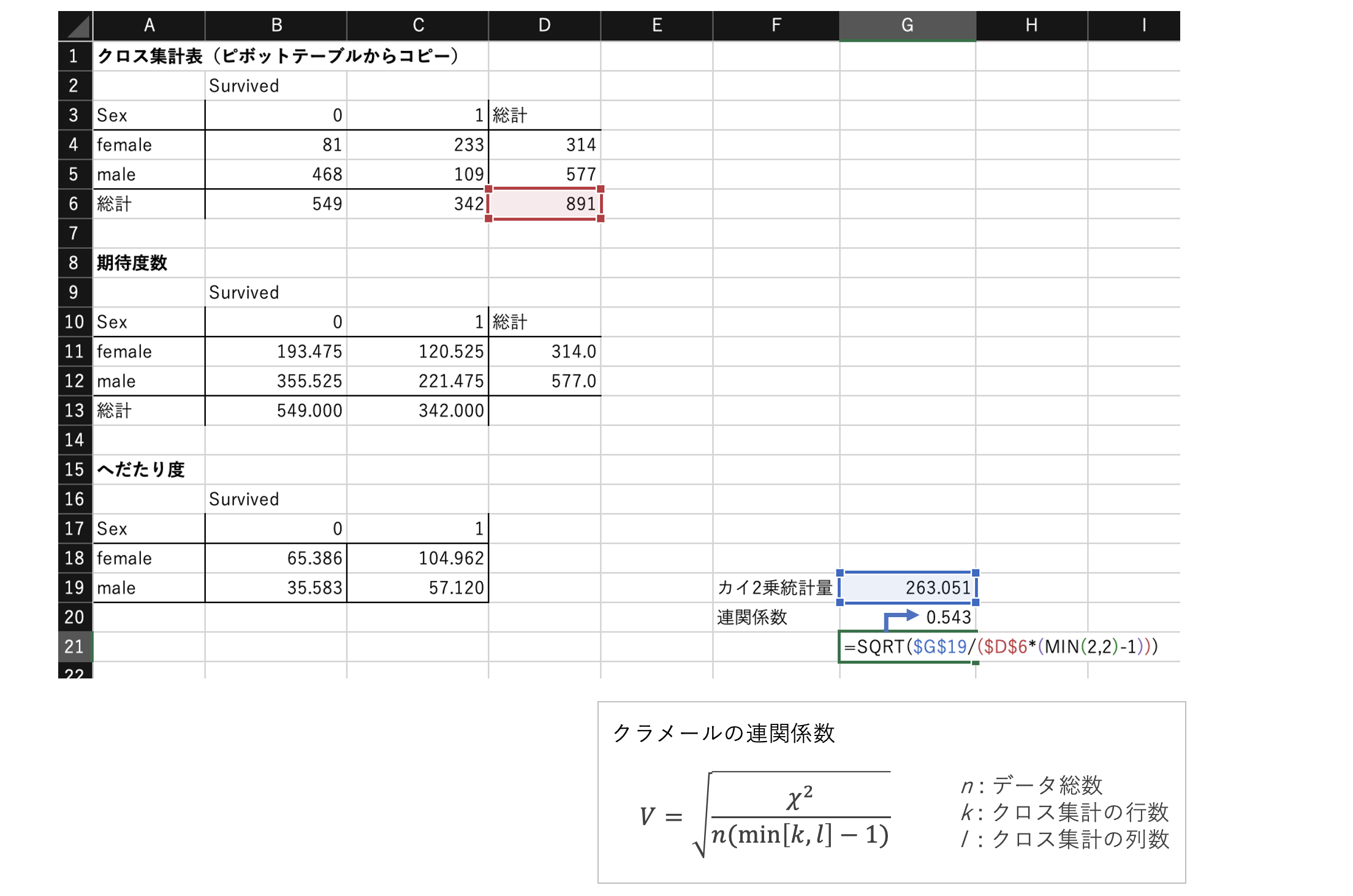
※参考
クラメールの連関係数：https://bellcurve.jp/statistics/glossary/1263.html

特化係数の算出

算出式に従い、数式を実装して求める。
※特化係数は、対象が全体と比較して「どのくらい特化しているか」という度合い。

例として、ある県の産業の特化係数を求める場合、
「ある県の対象産業の構成比 ÷ 全国の対象産業の構成比」で算出する。

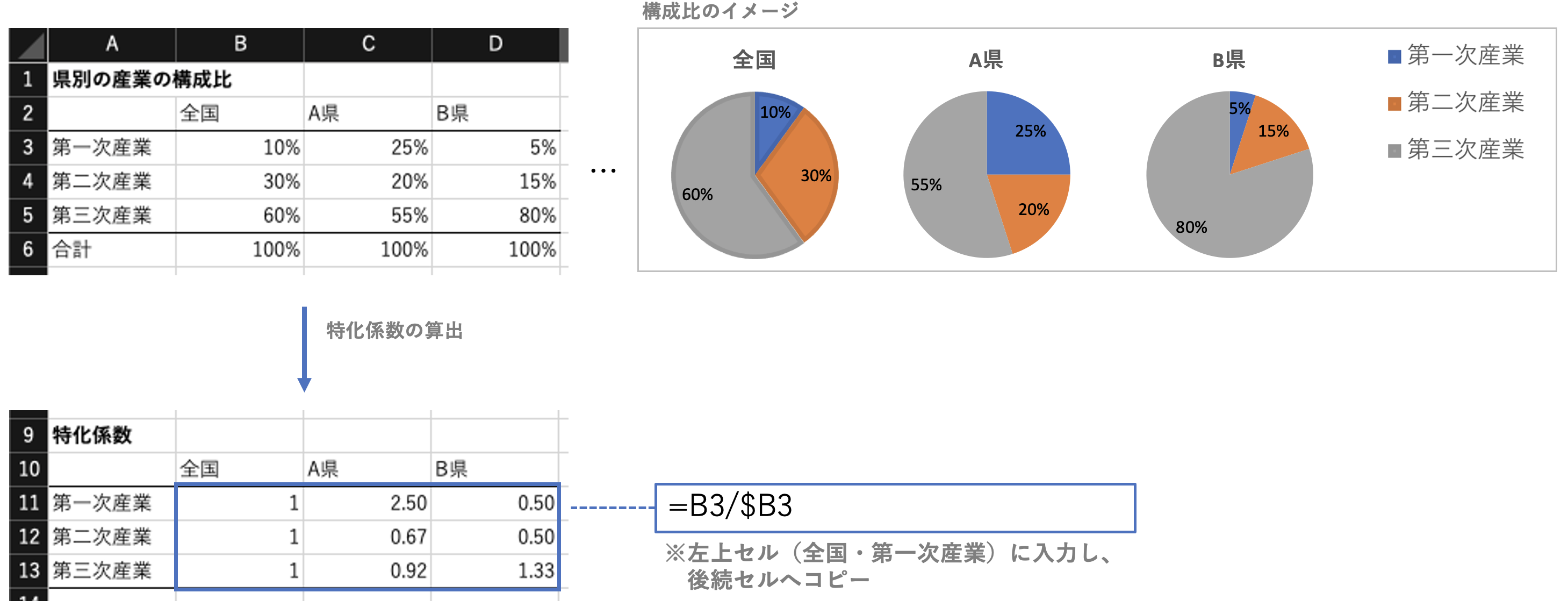
特化係数は、1.0を超えていればその県は全国平均に比べ相対的に○○産業に特化しているといえる。
上の例では、A県の第一次産業、B県の第二次産業は、全国構成比と比較して特化しているといえる。

多重クロス表の作成

前述の「クロス集計の作成」と同じ要領で作成する。
※多重クロス表は、複数のカテゴリが重ねて（多重に）作成したクロス集計表。
ここでは、Titanicデータの「Sex」×「 Pclass」×「Survived」で多重クロス表を作成する。

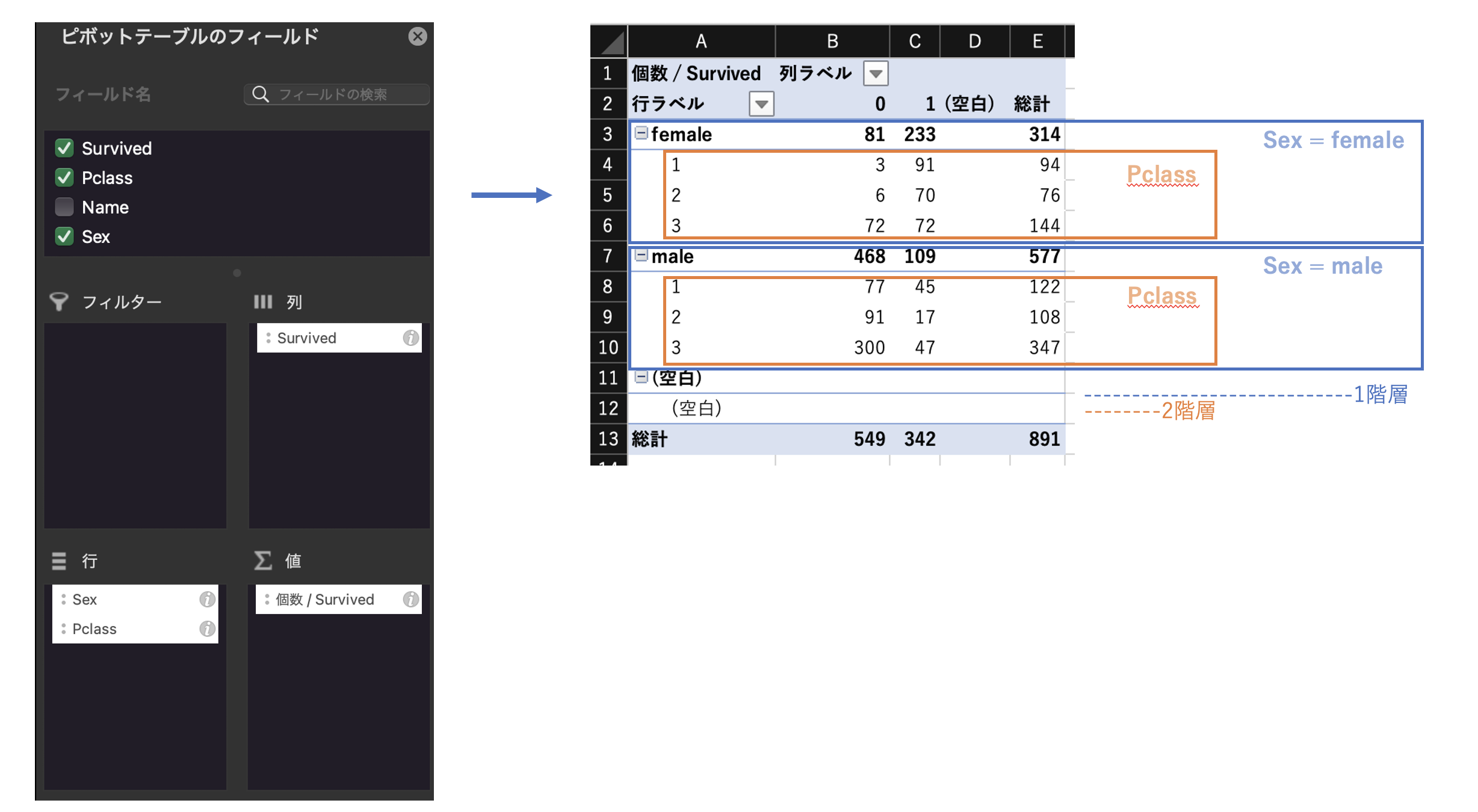
例えば、femaleのPclasss=3においては、生存と死亡の人数が同一（生存率が50％）となっており、生存率の高い女性でも、船室の等級が3の場合は生存率が五分五分であったことが分かる。

1変量の量的データの分析

度数分布表の作成

ここでは、Titanicデータの「Age」の度数分布表を作成する。

（データ分析ツールを使用）
データ分析＞ヒストグラムで度数分布表を作る。

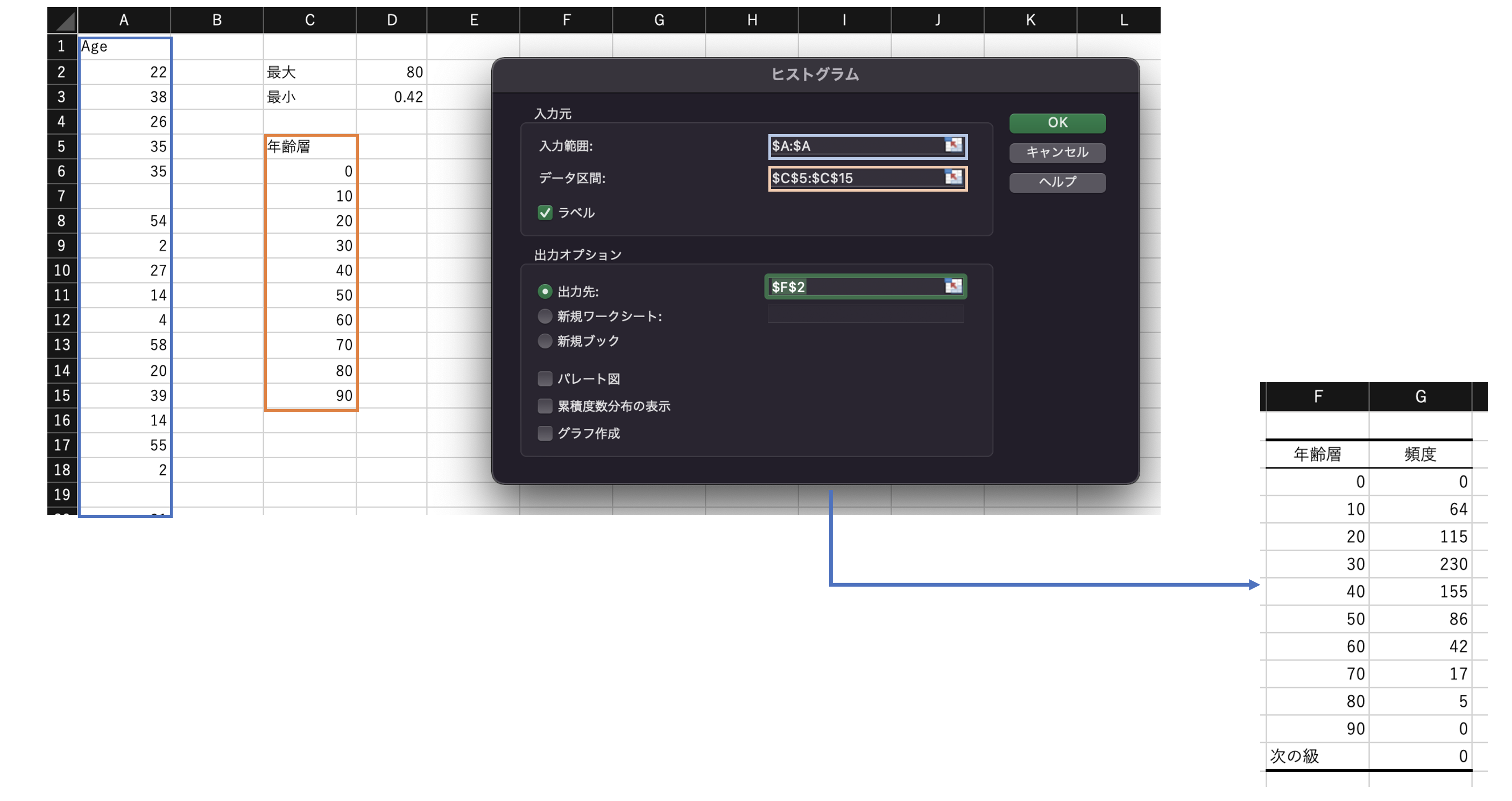
なお、「データ区間」を指定せずに実行することも可能。
※データ区間を指定しない場合は、自動的に、[(最大値−最小値)/√データ数]で計算され、 最小値 を下限値としてこの階級幅のデータ区間になる。

（ピボットテーブルを使用）
また、ピボットテーブルでも作成できる。
「フィールドのグループ化」により対象列を階級に区切る。

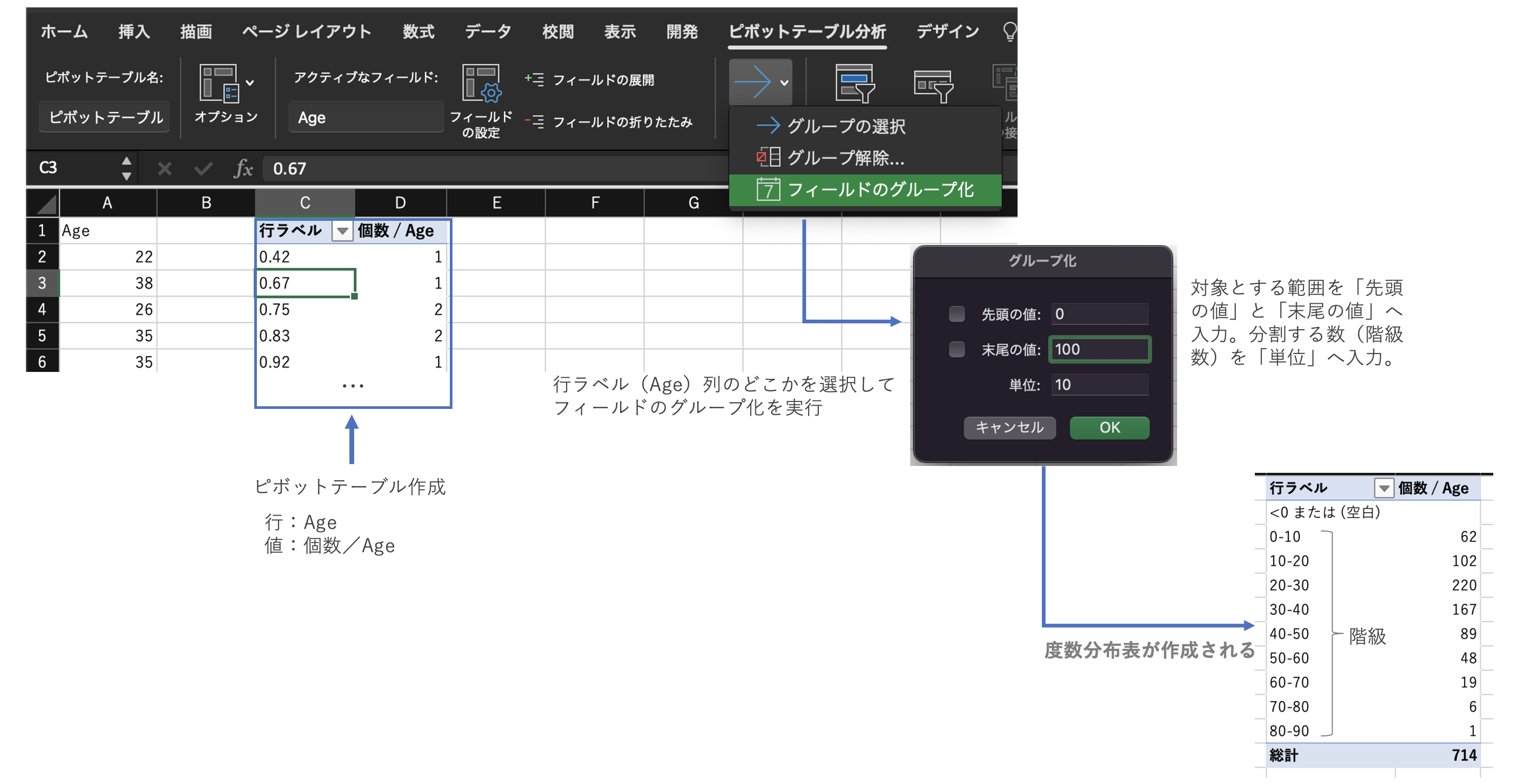
ヒストグラムの作成

得られた度数分布表をグラフ化すればヒストグラムとなる。

または、下記の方法でもヒストグラムは作成可能。

• 上記データ分析＞ヒストグラムの際に、「グラフ作成」にチェックする
• 対象列を選択し、挿入＞ヒストグラムでグラフ化する

基本統計量の算出

（データ分析ツールを使用）
データ分析＞基本統計量で、次のような項目を出力できる。

• 平均
• 標準誤差
• 中央値 （メジアン）
• 最頻値 （モード）
• 標準偏差
• 分散
• 尖度
• 歪度
• 範囲
• 最小
• 最大
• 合計
• 標本数

（関数を使用）

合計：SUM
平均値：AVERAGE
中央値：MEDIAN
最頻値：MODE.SNGL
分散：VAR.P、VAR.S　※Pは母集団の分散、Sは不偏分散
標準偏差：STDEV.P、STDEV.S ※Pは母集団の標準偏差、Sは不偏標準偏差
尖度：KURT
歪度：SKEW
範囲：MAX - MIN
最小：MIN
最大：MAX
標本数：COUNT
四分位： QUANTILE .INC （0: 0%、1:25%、2:50%、3:75%、4:100%） ※.EXCは0%と100%を含めない （1:25%、2:50%、3:75%）
パーセント点：PERCENTILE.INC

管理図

管理図は、データの準備が手間でグラフづくりは割愛。余力があればチャレンジする。
グラフのイメージと読み方（UCLより上、またはLCLより下にある場合にアウトとする等）について確認しておく程度に留めた。

※参考
管理図の作り方：https://kraken39s.com/qctest-control-chart#1

外れ値

外れ値については、試験としてはどの辺までの知識が問われるのかは不明。
ひとまずは、代表的な検出方法と対処方法を確認しておく。

外れ値の検出

外れ値は、次のような方法で検出する。

• ヒストグラムや散布図をもとに目視にて確認
• 箱ひげ図（の作成過程）で検出
  • 第1四分位数-1.5×IQRより小さい値
  • 第3四分位数+1.5×IQRより大きい値
• （正規分布するデータであれば）標準偏差から2倍や3倍を基準に検出

外れ値への対処

外れ値は、次のような方法で対処する。

• データ収集過程を考慮し、削ってもよい値であれば除外する。
• 入力ミス等であれば修正する。
• 分布の右裾が長い分布であるなど、状況により対数変換する。

2変量の量的データの分析

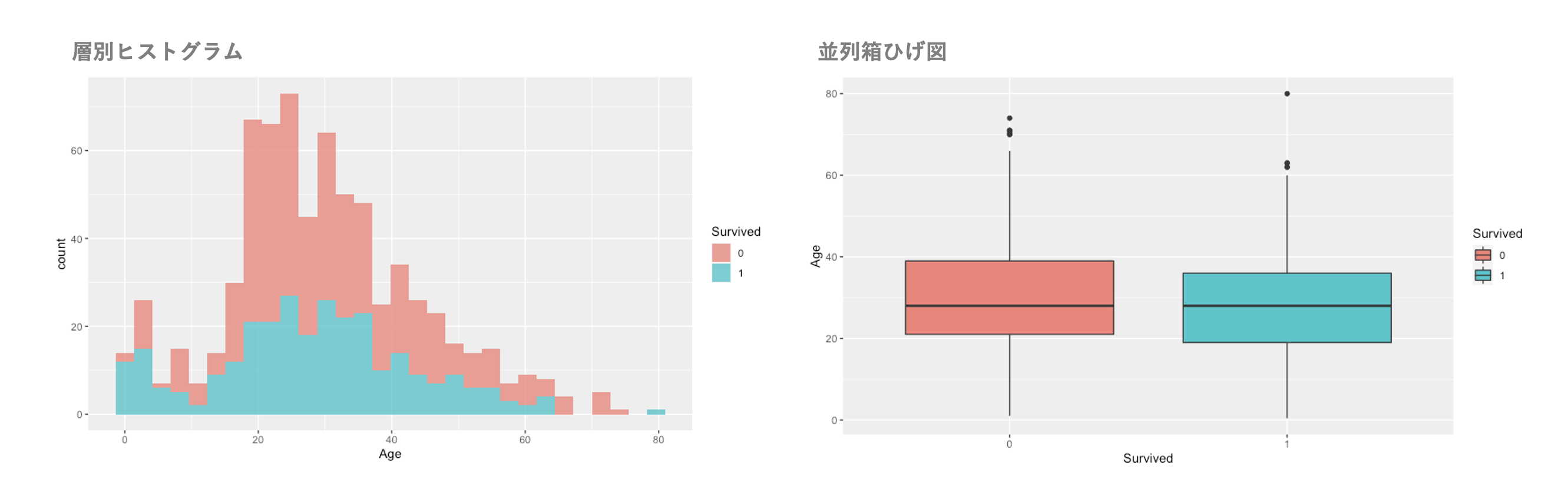
層別ヒストグラム、並列箱ひげ図

層別ヒストグラムや並列箱ひげ図は、次のようなイメージ。

上図はR言語で作成。並列箱ひげ図はExcelでも難しくないが、層別ヒストグラムの作図がちょっと手間だったので割愛（箱ひげ図も手抜きでRで描いた）。余力があればチャレンジする。

試験では、層別化した群間の差異などを比較する際に分布を図示する。

相関（相関係数、散布図）

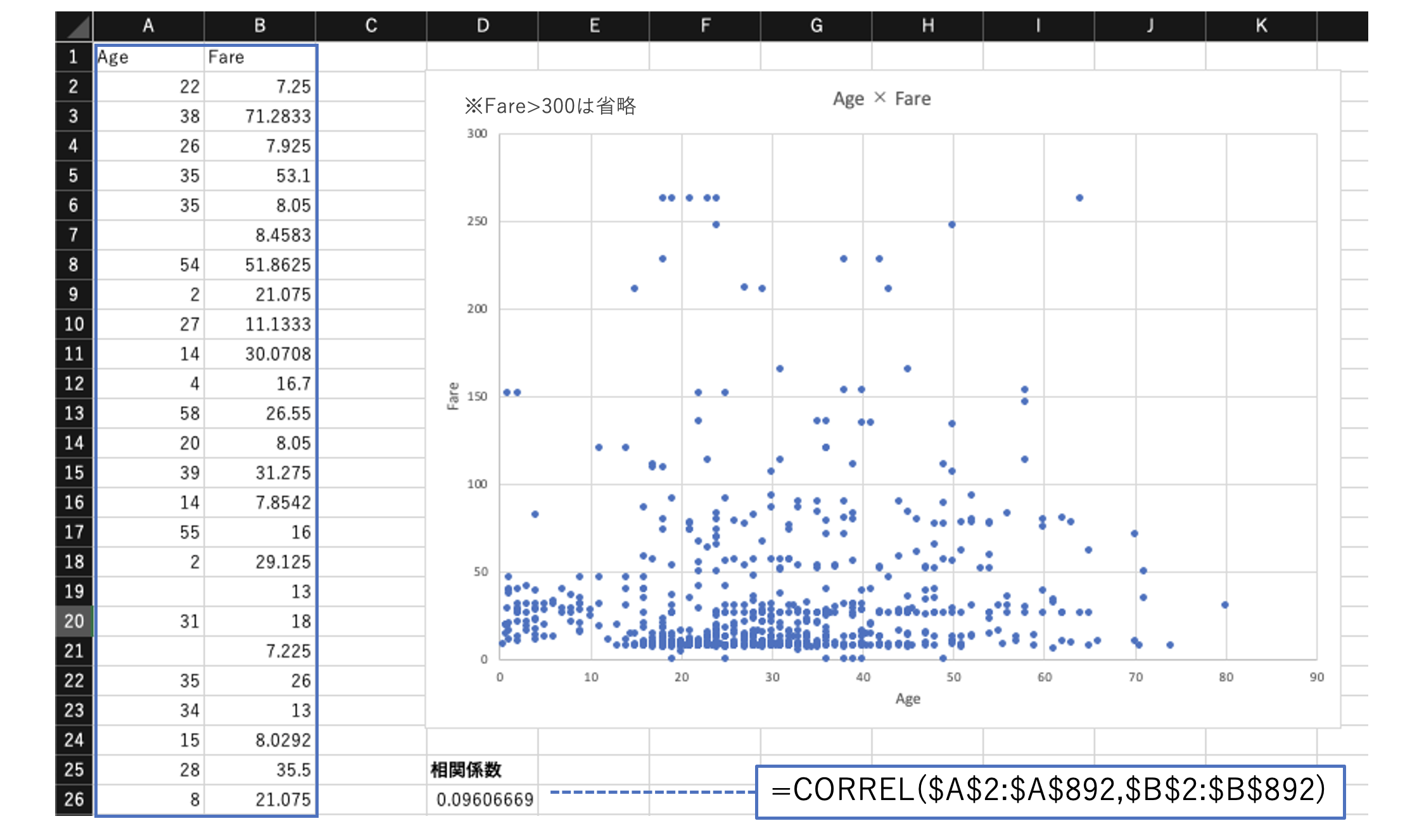
（散布図 ＋ CORREL関数）
2つの変数について、散布図の作成、および相関係数を算出する。

# 相関係数
CORREL（配列1, 配列2）

上記は、Titanicデータの「Age」×「Fare」の散布図と相関係数を求めている。
相関係数は0.096であり、ほぼ相関はない。

（分析ツールを使用）
データ分析＞相関係数でも相関係数を算出する。

こちらは3種以上のデータを入力できる。
各変数ペアの相関係数を求め表形式で出力する。

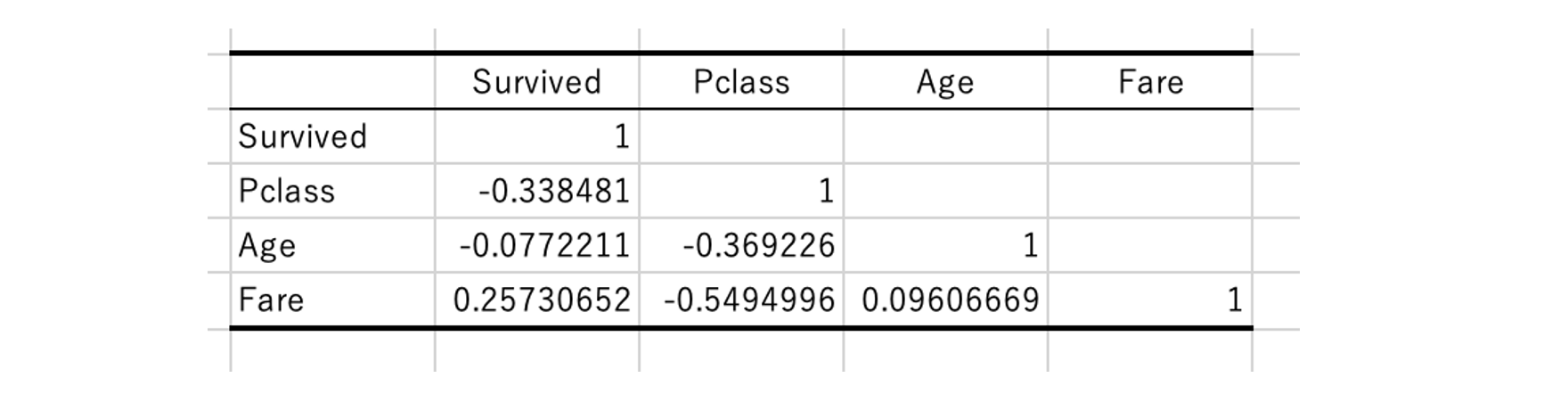
単回帰分析

下記の重回帰分析と同じ方法でも実行可能だが、ここではお手軽に散布図上で実行する。
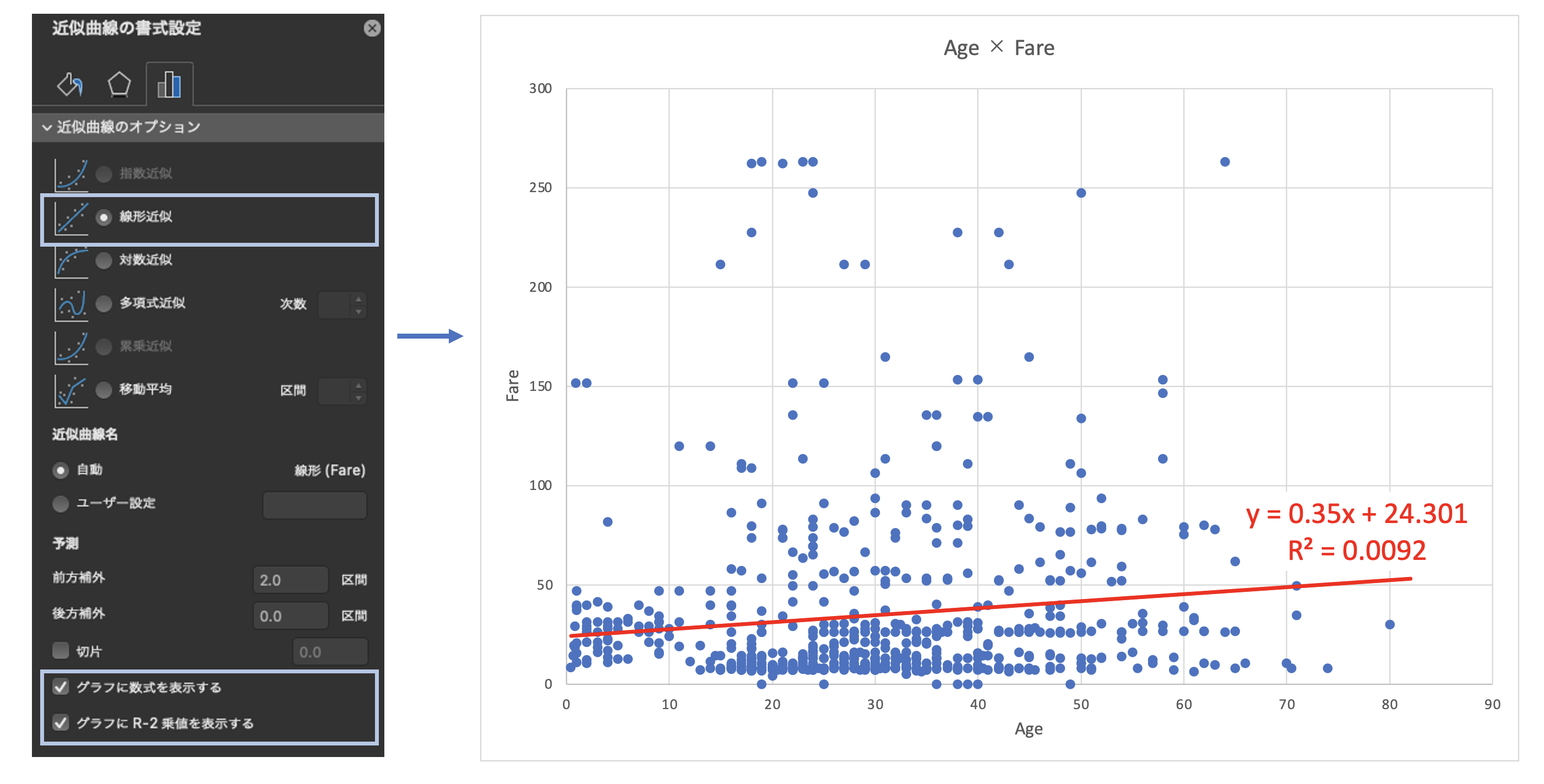
グラフ要素を追加＞近似曲線の追加＞線形近似で回帰直線を表示する。
また、下記にチェックすることで数式と精度(R2値）を表示することもできる。
「グラフに数式を表示する」
「グラフにR-2乗値を表示する」

上図では、Titanicデータの「Age」 ×「Fare」の散布図上で回帰分析を実施。

このケースでは、Fareを被説明変数（y）、Ageを説明変数（x）としている。
ここで

• xに掛けられている「0.35」が回帰係数
• R2乗値「0.0092」が寄与率（＝決定係数）

決定係数が0に近いため、AgeではFareをほとんど説明できていない事がわかる。

重回帰分析

データ分析＞回帰分析で重回帰分析を実行する。

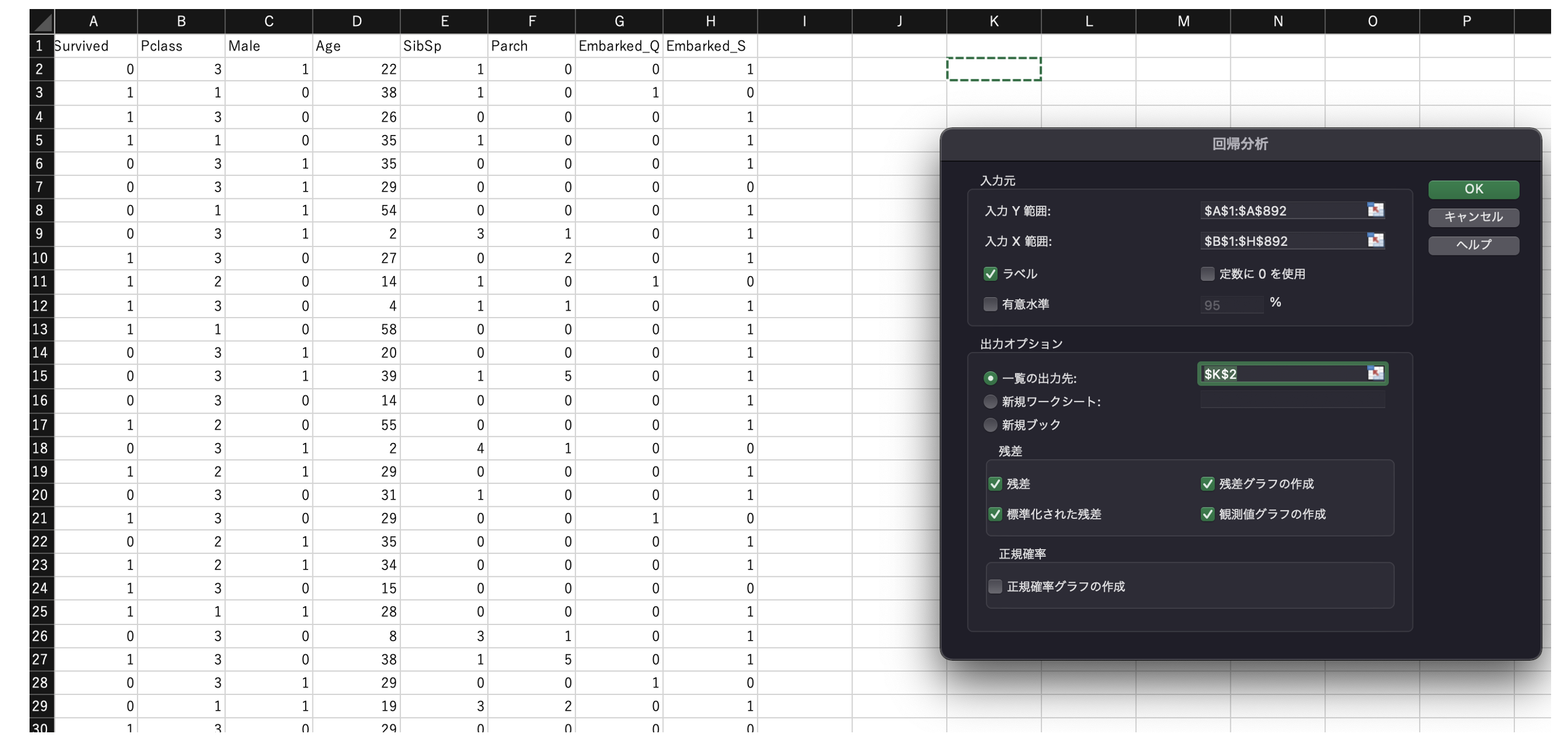
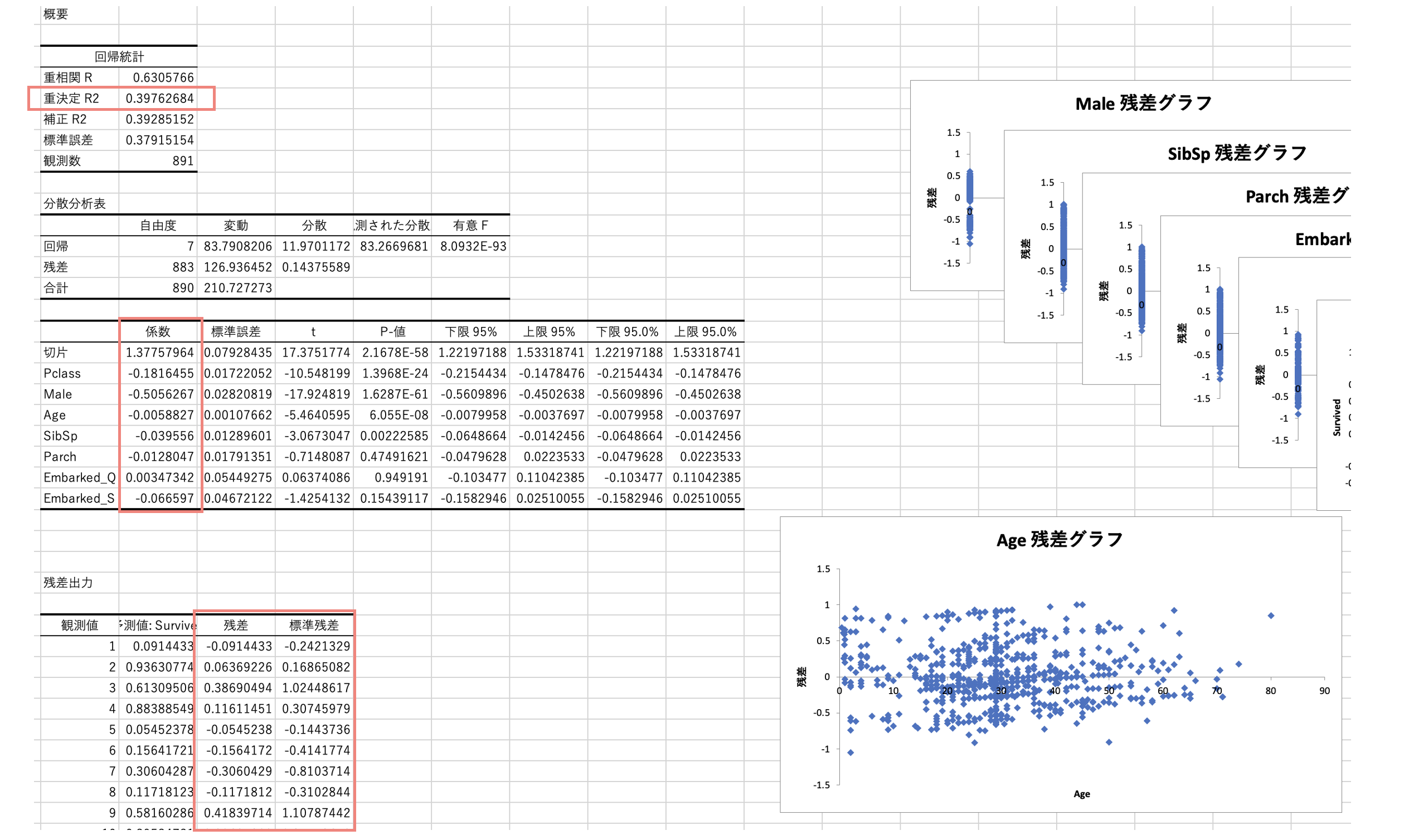
上図では、Titanicデータの「Survived」を説明変数（y）、他変数を説明変数（x）とした回帰分析を実施。
作成した説明変数は次の通り。

• 「Male」は、性別（Sex）が男性（male）の場合に1とした変数。
• 「Age」は、欠損を平均値で埋めた。
• 「Embarked_Q」「Embarked_S」は、EmbarkedがQまたはSの場合に1とした変数。（「Embarked_C」は多重共線性を考慮して除外）

回帰分析を実行すると、決定係数R2や回帰係数、残差などが出力される。

確率と確率分布

場合の数

下記の計算に用いる関数を確認しておく。

# 階乗
FACT(n)

# 順列
PERMUT(n,r)

# 組み合わせ
COMBIN(n,r)

ベイズの定理

ベイズの定理は、しっかり式を立てられることが重要。
式さえ立てられれば、上記の場合の数や四則演算で解ける。（Excelで一発で答えを出すような関数やツール等はない）

下記、統計WEB等に出てくる例題を、エクセル上で解いてみると良いかも。

※参考
ベイズの定理：https://bellcurve.jp/statistics/course/6444.html
ベイズの定理の使い方：https://bellcurve.jp/statistics/course/6448.html
練習問題：https://bellcurve.jp/statistics/course/7873.html

尤度

尤度は、想定した確率分布＆パラメータで、サンプルが得られる確率のこと。

例えば、コインを10回投げて表が5回出た場合に、もともとの表が出る確率pをパラメータとして尤度を求めてみる。
コインを複数回投げた際の「表が出る回数」の確率は二項分布に従うため、仮のパラメータpを設定し、サンプル値（試行回数と成功数=表が出た回数）を当てはめた二項分布の値が尤度となる。
尤度が最も高くなるパラメータを求めることが最尤推定。

※BINOM.DIST関数（二項分布）については後述。

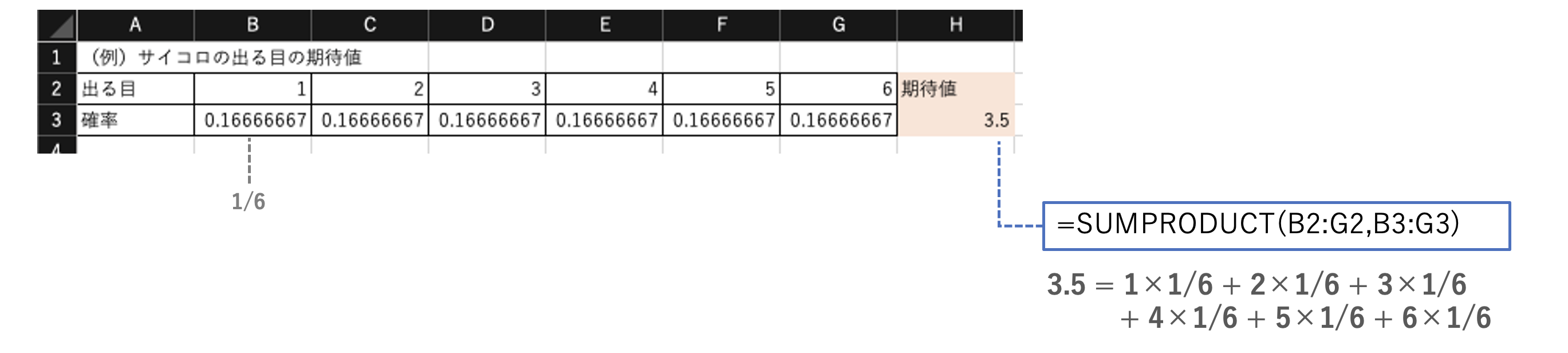
期待値

とくに難しいことはないが、配列同士の積和を求めるSUMPRODUCT関数を使うと計算が容易になるケースもある。

# 2つの配列の対応する要素同士を掛けた総和を求める
SUMPRODUCT(配列1, 配列2)

例えば、サイコロの出る目の期待値は次のように計算できる。

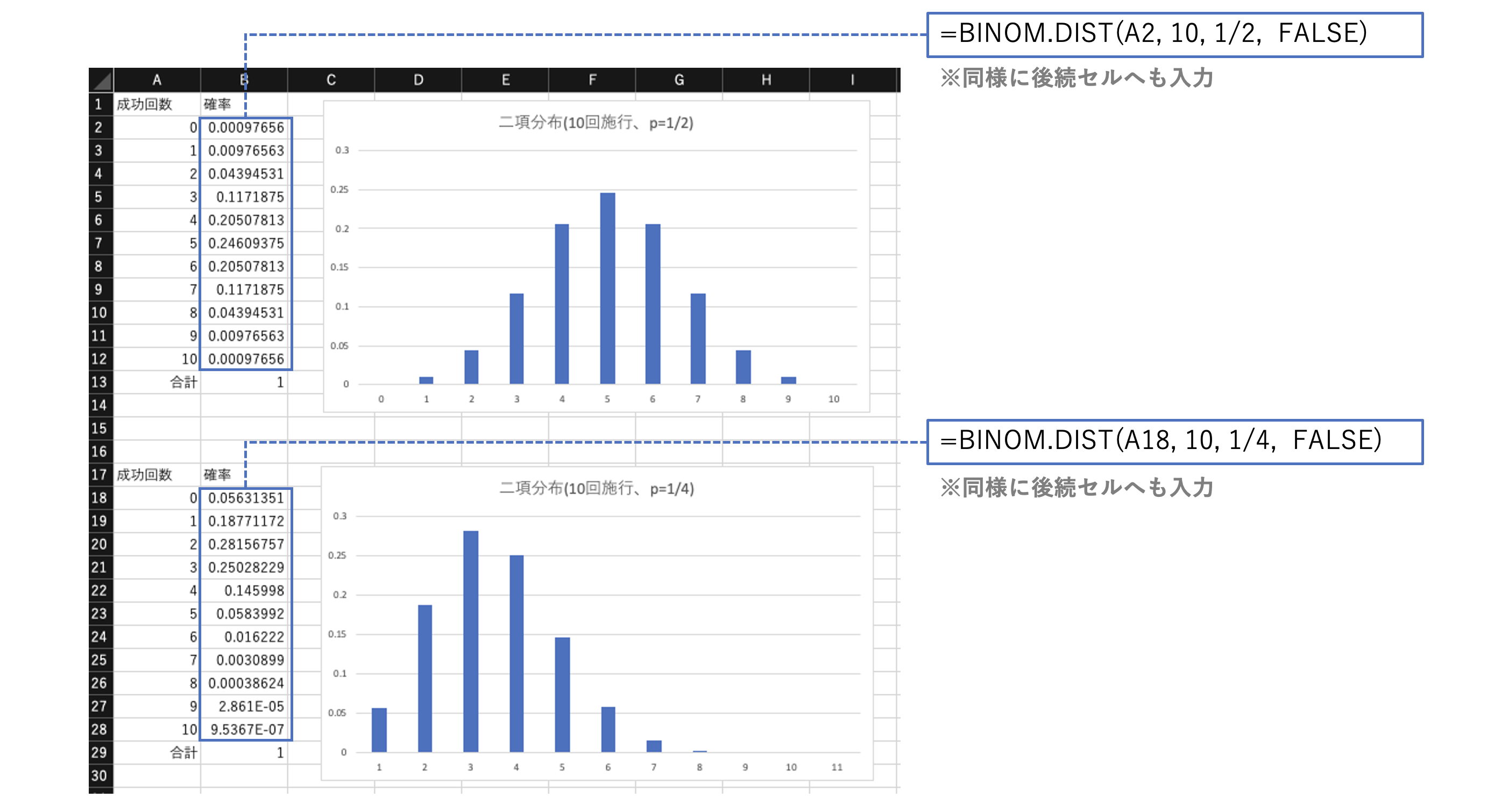
二項分布

二項分布は、n回のベルヌーイ試行（確率p）でk回成功する確率の分布のこと。
平均値と分散の式も確認しておく。

二項分布確率を取得する関数は次の通り。

# 二項分布関数の値を返す
BINOM.DIST(成功回数, 試行回数, 確率, 関数形式)

※関数形式は、TRUE：累積分布関数、FALSE：確率質量関数

（例：コインを10回投げて表が出る回数の確率）
上は表が出る確率pが1/2、下は表が出る確率pを1/4とした二項分布。

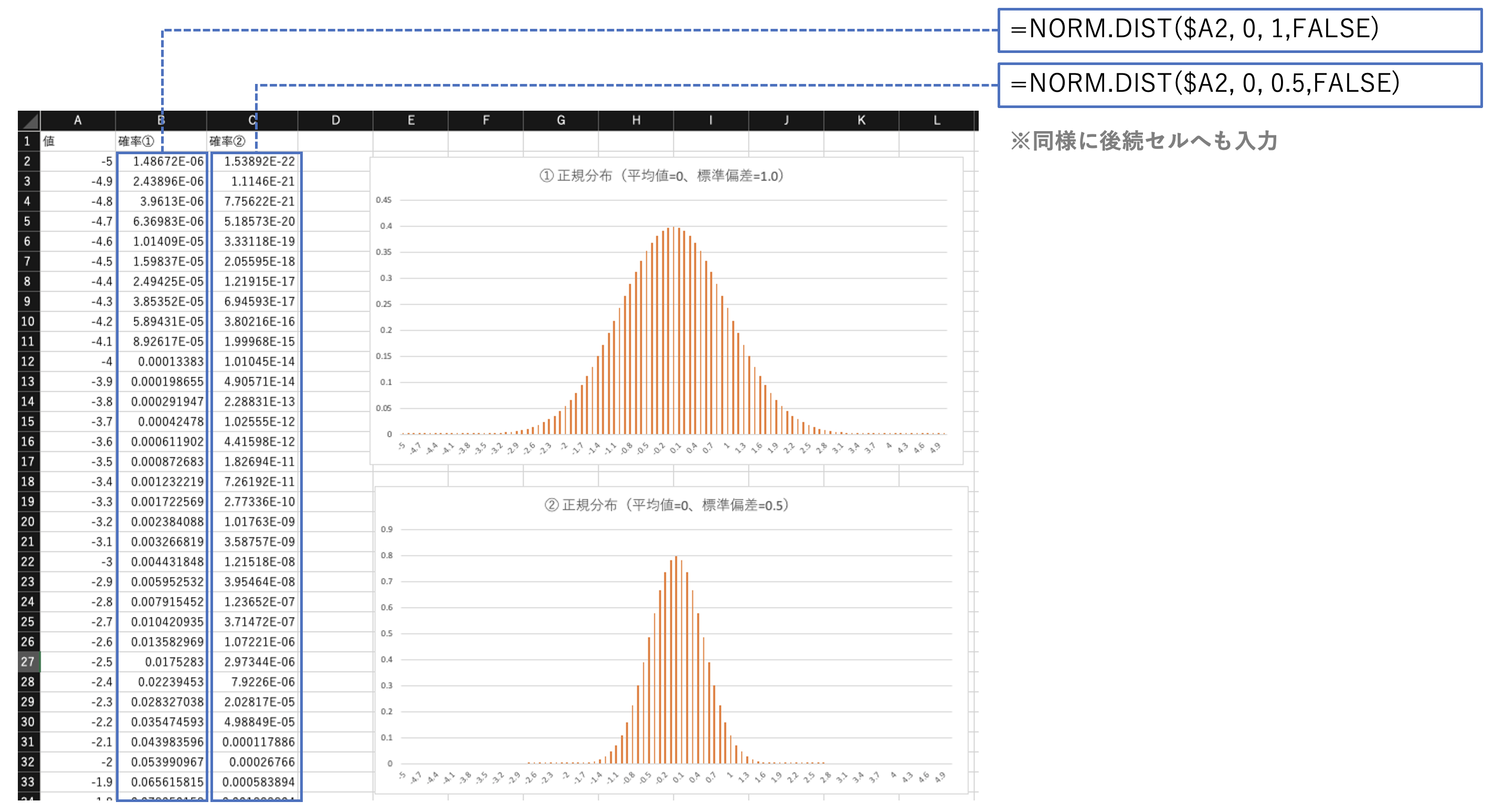
正規分布

正規分布の形、平均値と分散の式を確認しておく。

正規分布に関する関数は次の通り。

# 指定した平均と標準偏差に対する正規分布関数の値を返す
NORM.DIST(x, 平均, 標準偏差, 関数形式)

# 標準正規分布の累積分布関数の値を返す
NORM.S.DIST(z, 関数形式)

※関数形式は、TRUE：累積分布関数、FALSE：確率密度関数

# 正規分布の累積分布関数の逆関数の値を返す
NORM.INV(確率, 平均, 標準偏差)

（例：正規分布の形状）

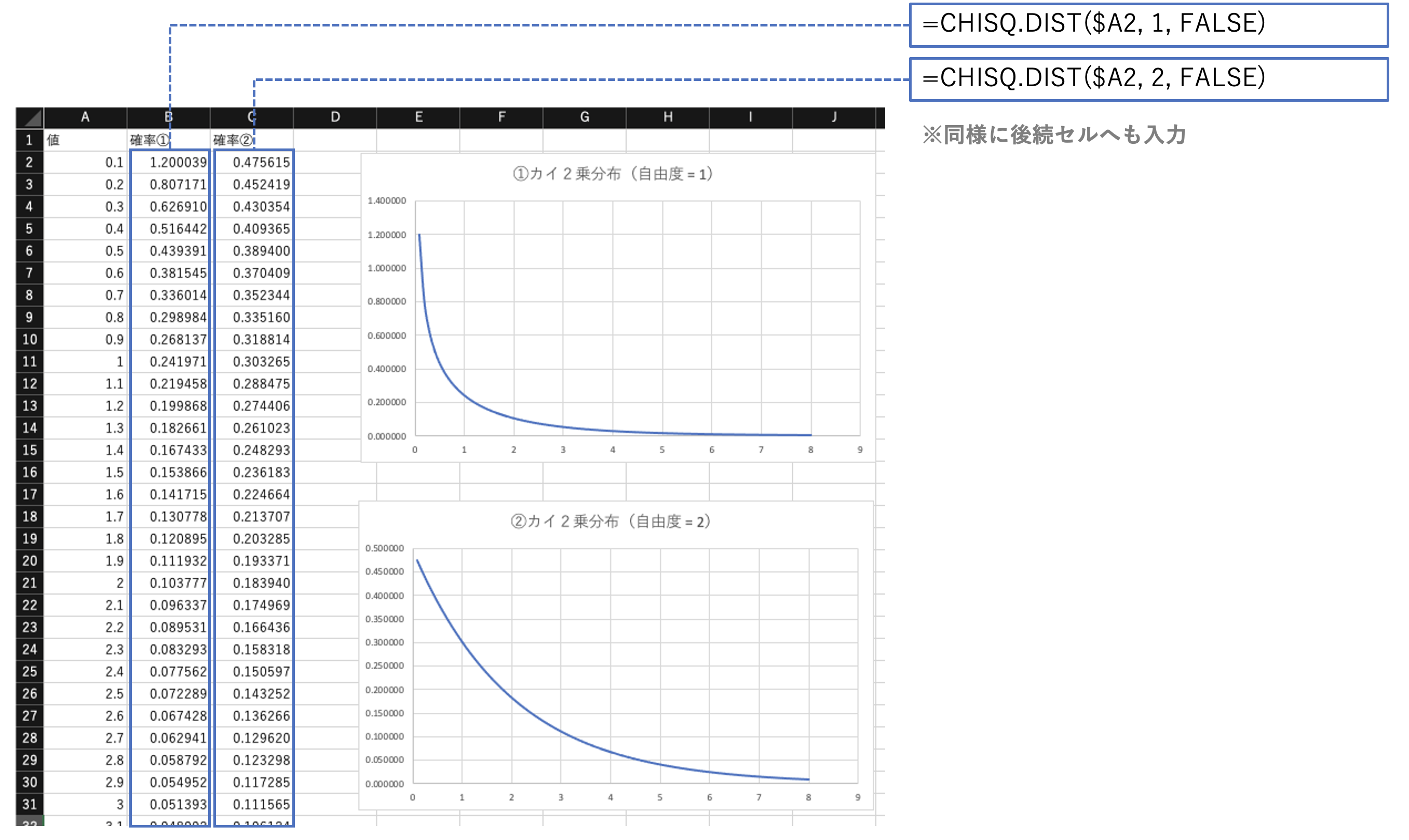
カイ２乗分布

カイ２乗分布の形、平均値と分散の式を確認しておく。

カイ２乗分布に関する関数は次の通り。

# 指定した自由度に対するカイ２乗分布関数の値を返す
CHISQ.DIST(x, 自由度, 関数形式)

※関数形式は、TRUE：累積分布関数、FALSE：確率密度関数

# カイ2乗分布の左側確率の逆関数の値を返す
CHISQ.INV(確率, 自由度)

（例：カイ2乗分布の形状）

推定

標本誤差

標本誤差は、標本値 - 母集団値。
母集団値は通常未知のため、標準誤差を用いる。

標準誤差

標準誤差SEは、標準偏差 ÷ √n。
nが大きいほどSEは小さくなる。
標準偏差はnが変化しても変わらないが、標準誤差は変わる。
（標準誤差では、まったく同じバラつきでもデータ数の大小により信頼性が異なってくる。）

信頼区間、信頼度

信頼区間（95%を例に）は、「母平均が、95％の確率で推定した信頼区間に含まれる」ではなく、「標本から信頼区間を求める作業を100回行うと、95回は母平均がその区間に含まれる」という意味。この「95」は信頼度（信頼係数）と呼ばれる。

信頼区間は次の特徴がある。

• 信頼係数が大きいほど、信頼区間の幅は広くなる
• サンプルサイズｎが大きいほど、信頼区間の幅は狭くなる

※参考
95％信頼区間のもつ意味：https://bellcurve.jp/statistics/course/8891.html

母平均の信頼区間（母分散が既知）

母分散が既知の場合は正規分布を用いて信頼区間を求める。
平均値x ± CONFIDENCE.NORM関数で計算する。

# 信頼区間を求める（正規分布を使用）
CONFIDENCE.NORM(有意水準α, 標準偏差, 標本数)

※両側での値（α/2の区間）を返す

CONFIDENCE.NORM関数を使用せずに解く場合は次の通り。

SQRT(分散 / データ数) * NORM.S.INV(α/2)

母平均の信頼区間（母分散が未知）

母分散が未知の場合はt分布を用いて信頼区間を求める。
信頼区間は、平均値x ± CONFIDENCE.T関数で計算する。

# 信頼区間を求める（t分布を使用）
CONFIDENCE.T(有意水準α, 標準偏差, 標本数)

※両側での値（α/2の区間）を返す

CONFIDENCE.T関数を使用せずに解く場合は次の通り。

SQRT(分散 / データ数) * T.S.INV(α/2)

母比率の信頼区間

※直接的に求める関数がないため、公式に沿って計算する。
信頼区間は、平均値x ± 下記式で求める。

SQRT(p * (1-p) / データ数) + NORM.S.INV(α/2)

※なお、信頼区間の幅が最も大きくなるのはp=0.5のとき。

検定

検定とは、サンプルから得られる結論（＝仮説）が、母集団でも成立するかをテストすること。

帰無仮説

否定したい仮説（無に帰したい説）

対立仮説

本来言いたい仮説

有意水準（危険率）

帰無仮説を棄却する基準。「滅多におきない事象」と判断する確率のしきい値。
p値が有意水準よりも小さいときに帰無仮説を棄却して対立仮説を採択する。
αで示され、分析者が決める。（一般的に0.05や0.1）

有意確率（p値）

帰無仮説が正しいと仮定したときに、観測した事象が起こりうる確率。

※参考
検定で使う用語：https://bellcurve.jp/statistics/course/9311.html
検定統計量と棄却域・採択域：https://bellcurve.jp/statistics/course/9317.html
両側検定と片側検定：https://bellcurve.jp/statistics/course/9319.html

第一種の過誤と第二種の過誤

試験としてはどの辺までの知識が問われるのかは分からないが、
とりあえず、それぞれの意味や対応策などを抑えておく。

（第一種の過誤 α ）
本当は正しいのに帰無仮説を棄却してしまう（「誤った対立仮説」を採択してしまう）という誤り。
通常の検定では、αのみを意識（0.05など設定）して比較を行っている。

（第二種の過誤 β ）
本当は誤ってるのに帰無仮説を棄却しない（「正しい対立仮説」を採択できない）という誤り。
βは、通常の検定ではケアされない。

（βの特徴）
帰無仮説を表現する分布と対立仮説を表現する分布が離れているほどβは小さくなる。
また、それら分布の差が一定の条件では、

• データのバラつきが小さいほど
• サンプルサイズが大きいほど
• 有意水準αが高いほど

Βは小さくなる。

（αとβのトレードオフ）
なお、αとβはトレードオフのため、常にどちらかの誤りが発生する可能性がある。
そのため、検定の結果のみで判断せずに、グラフによる可視化での比較なども交えて判断するのが良い。

※参考
第1種の過誤と第2種の過誤：https://bellcurve.jp/statistics/course/9315.html

2項検定

本来pの確率の事象が、N回施行した中でk回発生するケースにおいて、確率pが有意に大きいかを検定する。
次の式でp値を求め、有意水準α（0.05など）と比較する。αより小さければ有意。

1-BINOM.DIST(k-1, N, p, TRUE)
（k-1回の累積確率を求めて1から引けばk回位置のp値が求まる。）

※ 片側検定。両側の場合は上記で求めたp値を2倍する。

確率pが有意に小さいかを求める場合は、次の式でp値を求める。

BINOM.DIST(k, N, p, TRUE)

Z検定

標本の平均と母集団の平均とが統計学的にみて有意に異なるを検定する。
次の式でp値を求め、有意水準α（0.05など）と比較する。αより小さければ有意。

Z.TEST(サンプル配列, μ0, [σ])

※μ0は、母集団の平均値（検定する値）。σは、母集団の標準偏差（省略するとサンプル配列の標準偏差が使用される）
※戻り値は、片側確率のp値。

両側検定でのp値は次の式で求める。

2 * MIN(Z.TEST(…), 1 - Z.TEST(…))

t検定

2群の平均値が優位に異なるかを検定する。
群間の対応あり／なし、および分散の一致性により、検定手法を切り替える。
等分散性は、F検定で事前に確認するのも手。（F検定はF.TEST関数で実行可能）

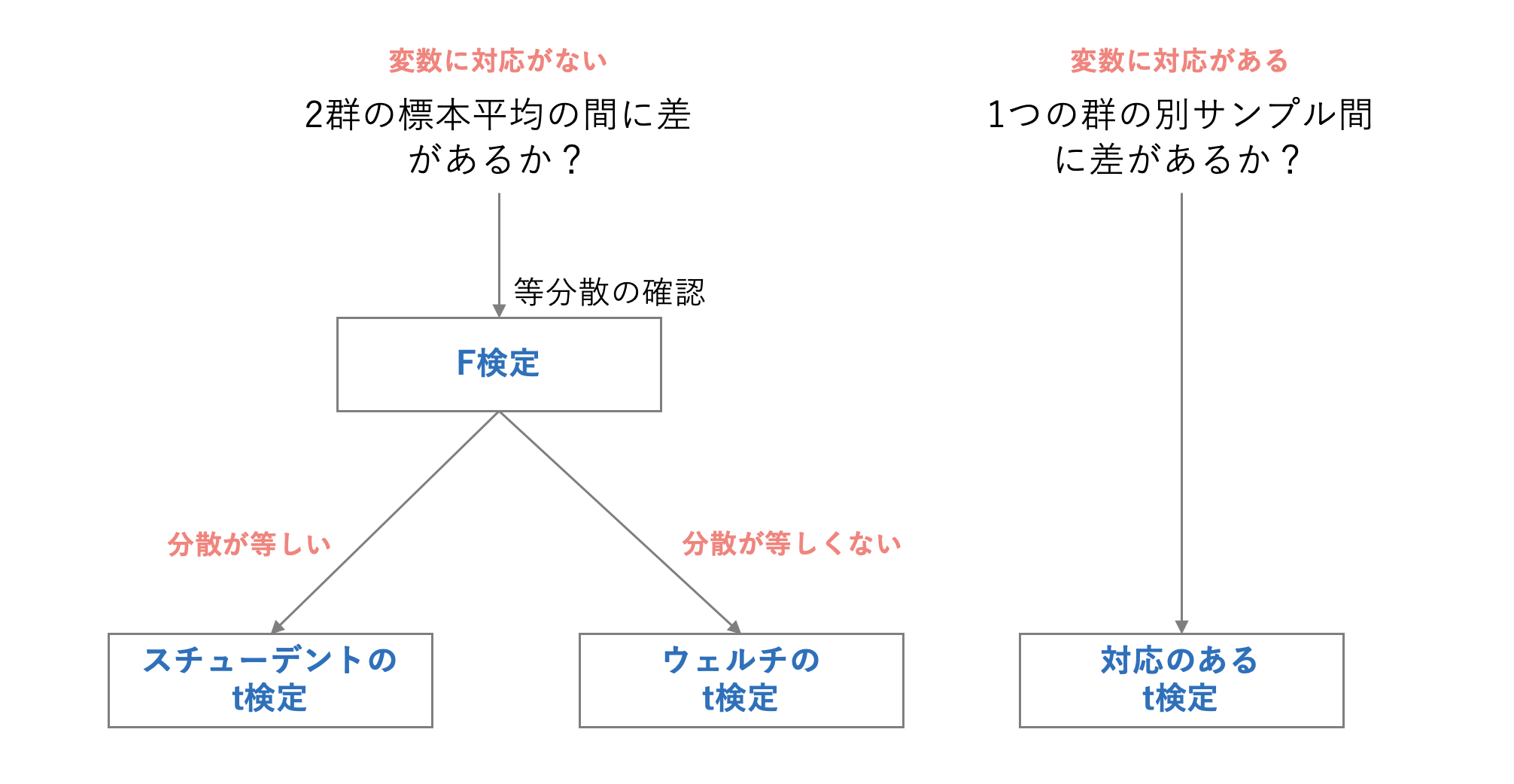
t検定は、
次の式でp値を求め、有意水準α（0.05など）と比較する。αより小さければ有意。

T.TEST(サンプル配列１,サンプル配列本２, 片側・両側の指定, t検定の種類)

※引数について
片側・両側の指定：
  1 片側
  2 両側

t検定の種類：
  1　標本間に対応のあるt検定
  2　等分散を仮定した２標本による検定（スチューデントのt検定）
  3　分散が等しくないと仮定した２標本による検定（ウェルチのt検定）

※参考
実際、ウェルチのt検定は、等分散であってもそうでなくても使うことができる。
が、検定手法を切り分けるのは、等分散を仮定できる場合はスチューデントのt検定の方が有意さが出やすくなるため、そちらを使わないのはもったいないというモチベーションから来る。

カイ2乗検定

カテゴリデータ×カテゴリデータの関連性を検定する。

次の式でp値を求め、有意水準α（0.05など）と比較する。αより小さければ有意。

CHISQ.TEST(実測値配列, 期待値配列)

※期待値配列は自分で作成しておく必要あり。
（「へだたり度」や「カイ２乗統計量」はこの関数がやってくれる）

前述の「クロス集計の作成」で作成した表をもとに計算してみると次の通り。

時系列データの分析

指数

とくにExcelの関数等はないので、単純な計算で求める。
指数 = ある時点の値 ÷ 基準時点の値

（例）

• 　x年度の売上 / 2010年度の売上
• 　x月時点の体重 / 1月時点の体重
• 　x回目の点数 / 1回目の点数

移動平均

一定期間（過去の複数時点）の平均値を1時点ずつずらしながら平均値を求める。
AVERAGE(過去の複数時点の値配列)

移動平均は、データ分析＞移動平均でも算出可能。
実行すると、出力先のセルへAVERAGE関数が埋め込まれる。

伸び率

とくにExcelの関数等はないので、単純な計算で求める。
伸び率 = (ある時点の値 - 起点となる時点の値）÷ 起点となる時点の値

（例）
*　（今年度売上 - 前年度売上）/ 前年度売上
*　（今月の体重 - 先月の体重）/ 先月の体重
*　（今回の点数 - 前回の点数) / 前回の点数

成長率

前年対比の成長率といえば、
今年度の値 ÷ 前年度の値
というように指数を計算した値。

（例：前年度の売上が140に対し、今年度が100だったときの成長率）
1.4 = 140 / 100

1を引き算して「0.4」を求め、「前年に対し40%成長」と表現することもあるし、成長率は、伸び率と同じ計算で求めるときもある。

平均成長率

各時点で求めた成長率の幾何平均値。
(x1 * x2 * x3* … *xn) ^ (1 / n)

※ x ^ (1/n)は、xの1/n乗を計算している。

平均成長率は、福利の考え方を前提にしているので、各時点の成長率は足すのでなく掛ける。

（例：過去三年間の成長率が、1.4、1.2、1.6で求められたときの平均成長率）
1.39 = PRODUCT(1.4,1.2,1.6)^(1 / 3)

季節調整

季節調整は、ざっくりとは下のような手順で実行。

（移動平均を用いる方法）

1. 移動平均を求める（季節性を意識して）

2. 季節変動値（季節要因）を求める

   • 対象 ÷ 移動平均値

3. 季節指数を求める

   • 季節変動値のトリム平均を求める（トリム平均は、最大と最小を除外して計算する平均）

   • トリム平均の合計が移動平均の区間の値となるよう補正する

     → この補正値（補正トリム平均）を季節指数とする

4. 元データを季節指数で割って季節調整済みの値とする

※参考

実際に計算練習してみたい場合はこちらのサイトが参考になる。（とても分かりやすい）
https://www.winschool.jp/tips/detail133.html

テキストマイニング

Excelで実装可能なものは少ないので、、、正直何が出題されるか分からない。

文字列操作のExcel関数

ざっくりと文字列操作の関数を集めてみた。
（試験に関係なく便利な関数もあるので覚えておくと良いかも）

# 文字列検索
FIND(検索文字列, 対象, [開始位置])

※検索対象が検索文字列の最初に現れる位置を返す。見つからない場合はエラー。

# 文字列抽出（文字列の先頭＝右から指定した文字数の文字を返す）
LEFT(文字列, [文字数])

# 文字列抽出（文字列の指定位置から指定した文字数の文字を返す）
MID(文字列, 開始位置, 文字数)

# 文字列抽出（文字列の末尾＝左から指定した文字数の文字を返す）
RIGHT(文字列,[文字数])

# 文字列置換（位置指定）
REPLACE(文字列, 開始位置, 文字数, 置換文字列)

# 文字列置換（文字列指定）
SUBSTITUTE(文字列, 検索文字列, 置換文字列, [置換対象])

# 全角の英数カナ文字を半角へ変換する
ASC(文字列)

# 英字を大文字に変換する
UPPER(文字列)

テキストマイニングの手法

クリーニングや形態解析、構造データ化、適用可能な分析手法（クラスタリングや感情分析など）を用語レベルで抑えておくと良いのではないかと思う。

思いつく項目をいくつか挙げておく。

• 文字ゆらぎの解消
• 正規表現
• テキストの抽出・フィルタリング（特定文字列が含まれるテキストなど）
• 分かち書き
• 形態素解析
• ストップワード
• 品詞によるフィルタリング（名詞、動詞などの品詞にデータを絞り込む）
• bag of words
• TF-IDF
• 単語頻度の算出
• KWICコンコーダンス
• ワードクラウド
• 共起語・共起ネットワーク
• トピックモデル
• 感情分析（ポジティブ・ネガティブ等へのテキスト分類）
• クラスタ分析（階層型, 非階層型）

※参考
テキスト分析を分析する「テキストマイニング」をわかりやすく解説：https://data-viz-lab.com/textanalytics

おわりに

冒頭にも述べたとおり、
理論に力を入れすぎるよりも、Excelでゴリゴリ手を動かしておくのが重要（たぶん）。
関数をしっかり覚えて、実際のデータで繰り返しトレーニングすればきっと大丈夫。