[WIP] Mordred記述子の意味の一覧

注意: この記事はまだ作成途中ですが、仕上がっている部分までを公開しています。今後更新を進める予定です。

概要

Mordred記述子の内容はすべてここに書かれています。

Descriptor List
https://mordred-descriptor.github.io/documentation/master/descriptors.html

ただ、リンク先の関数等をぱっと見ただけだと何を示しているのか分からないものや、分かってもどう解釈すれば良いかが不明なものがあったので、分かる範囲でまとめてみました。
（以下の文中で単に「List」と書いたときは、上記リンク先のことを指します。）

環境

• Python 3.6.8
• Mordred 1.2.0

2D記述子

2Dと3Dを合わせた1826個中、1613個
番号はListによる。
例として以下の化合物を使用する。
エラー (無視すると欠損値となる) に関する記述には赤色を使う。

#1 - #4

• ABC
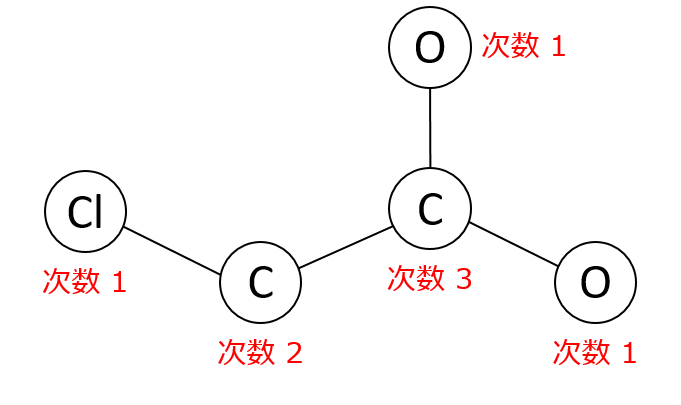
  Atom-bond connectivity index（Estrada, et al., IJC-A, 1998）を示す。
  水素を除いた化合物グラフ $G = (V, E)$ について、各頂点 $v_i \in V$ の次数（その頂点から出ている辺の数）を $d_i$ とすると、

ABC(G) = \Sigma_{e_{ij}\in E}\sqrt{\frac{d_i+d_j-2}{d_id_j}}

で表される。
例: モノクロロ酢酸の場合は以下のようなグラフとなる（多重結合でも辺は1本と考える）ため、 $ABC(G) = \sqrt{\frac{1+2-2}{1\times2}} + \sqrt{\frac{2+3-2}{2\times3}} + \sqrt{\frac{1+3-2}{1\times3}} \times 2= 3.047$ となる。

<解釈等>
同じ頂点数なら、枝分かれ/環構造が多いほど大きな値となる。
元論文によると、アルカンの場合、ABCの値と生成熱に高い正の相関（$R > 0.99$）がある。

• ABCGG
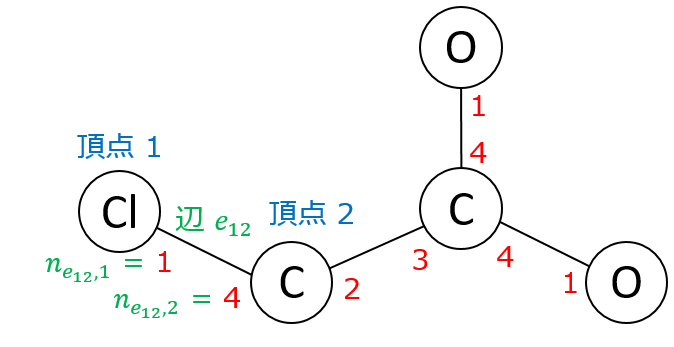
  Graovac-Ghorbani atom-bond connectivity index (Furtula, MATCH Commun. Math. Comput. Chem., 2016) という、ABCを発展させたもの。
  水素を除いた化合物グラフ $G = (V, E)$ の各辺 $e_{ij} \in E$ について、以下の数を定義する。

  $n_{e_{ij}, i} = (頂点iとの距離が、頂点jとの距離より近いような頂点の個数)$
  $n_{e_{ij}, j} = (頂点jとの距離が、頂点iとの距離より近いような頂点の個数)$

  これらについてABCのような式で、各辺について和をとる。

ABCGG(G) = \Sigma_{e_{ij}\in E}\sqrt{\frac{n_{e_{ij}, i}+n_{e_{ij}, j}-2}{n_{e_{ij}, i}n_{e_{ij}, j}}}

(例) モノクロロ酢酸の場合は各 $n_{e_{ij}, i}$ が以下のようになるため（自分自身もカウントすることに注意）、 $ABCGG(G) = \sqrt{\frac{2+3-2}{2\times3}} + \sqrt{\frac{1+4-2}{1\times4}} \times 3= 3.305$ となる。

<解釈等>
ABCと同様に、同じ頂点数なら、枝分かれ/環構造が多いほど大きな値となる。
元論文によると、オクタン異性体におけるエントロピーやAcentric factorとの相関が、ABCより高い。

• nAcid, nBase
  酸性官能基および塩基性官能基の個数。ListにSMARTSの正規表現あり。
  一例として、-COOH (に近いもの) や陰イオンが酸性官能基、アミンや陽イオンが塩基性官能基として扱われる。

<解釈等>
ブレンステッドやルイスの酸/塩基の定義に従うなら、陽イオンと陰イオンは逆のような気がするが…。
SMILESは水素を省略するから、なのかもしれない (例えば[Cl-]とだけ書かれていたら、それは[H+].[Cl-]の省略形 → 酸)。

隣接行列の固有値・固有ベクトル関連 (#5 - #16)

水素を除いた化合物グラフについて隣接行列 (Adjacency matrix, 頂点 $i, j$ をつなぐ辺があるなら $a_{ij}=1$ 、ないなら $a_{ij}=0$ であるような行列 $A = (a_{ij})_{ij}$ ) を考える。
この行列の固有値および固有ベクトルは、頂点の番号の付け方によらず一定であり、それを元に記述子を作っている。
隣接行列の固有値のことを、グラフのスペクトルとも呼ぶらしい。
(例) 酢酸の場合

$A$の固有値を計算すると $\lambda=-\sqrt{3}, 0, 0,\sqrt{3}$ と求められる。
対応する固有ベクトルはそれぞれ $$

行列に対する記述子の定義式はここにまとまっている (隣接行列に対してはSM1のみ使われない (*)) ので、意味のみを書いていく。
https://mordred-descriptor.github.io/documentation/master/matrix.html#matrix-aggregating-methods

• SpAbs_A
  固有値の絶対値の和。

• SpMax_A
  固有値の最大値。

• SpDiam_A
  固有値の最大値と最小値の差 (スペクトルギャップというらしい) 。

• SpAD_A
  固有値を平均が0になるように変換した際の、絶対値の和。

• SpMAD_A
  SpAD_Aを原子数 (=固有値数) で割ったもの。(*)

• LogEE_A
  式を参照。

• VE1_A

カウント系 その1 (#17 - #35)

• nAromAtom, nAromBond
  芳香族の原子/結合の個数。元のSMILESがケクレ表記・非ケクレ表記かに関係なく計算される。
  ヒュッケル則を満たさない化合物 (π電子数が4n個のもの) は、たとえ「c1ccc1」のように小文字 (非ケクレ表記) で書いていても、芳香族ではないものとして扱われる。

• nAtom
  原子およびイオンの数。

• nHeavyAtom
  水素以外の原子およびイオンの数。プロトンは含む。

• nSpiro
  スピロ原子 (2つの環が結合を共有せず1原子のみを共有しているとき、その原子を指す) の数。

• nBridgehead
  橋頭位原子 (2つの環が2本以上の連続する結合を共有しているとき、その共有部分の両端の原子を指す) の数。

• nHetero
  ヘテロ原子 (炭素・水素を除く原子) およびそれらのイオンの数。

• nH, nB, nC, nN, nO, nS, nP, nF, nCl, nBr, nI
  それぞれ水素、ホウ素、炭素、窒素、酸素、硫黄、リン、フッ素、塩素、臭素、ヨウ素原子の数。イオン化しているものも含む。

• nX
  ハロゲン原子 (17族の原子) の数。

トポロジカル記述子 (原子パラメータ系) (#36 - #641)

化合物をグラフ構造と見なし (水素原子も含む) 、各原子のパラメータ (例: 電気陰性度、原子番号) を用いて計算している。

ATS (#36 - #134)

「Moreau-Broto autocorrelation descriptor」としても知られる記述子。
(11原子パラメータ) × (9距離) の合計99個が存在する。
記述子名は「ATS[原子パラメータ][距離]」という表記になっている。

原子パラメータ

グラフ上の原子1つに対して1つの値を与える。基本的に原子種が同じならば違う位置にある原子でもパラメータは同じになるが、そうでないもの (周囲の原子の影響を受けるなど) (下の一覧では青色で示す) もある。

• dv
  Listにはvalence electrons (価電子) と書かれているが、一般的な価電子数ではなく、

\frac{(最外殻電子数)}{(原子番号)-(最外殻電子数)-1}

の値となっている (ただし水素は0、ヘリウムは2) 。
定義より第2周期 (Li ～ Ne) では最外殻電子数に一致する。

• d
  その原子とつながっている重原子 (水素以外の原子) の個数。
• s
  固有状態。
• Z
  原子番号。
• m
  原子量。
• v
  ファンデルワールス体積 (単位: $Å^3$) 。ファンデルワールス半径内部の体積なので、いわゆる「原子の大きさ」より大きい値になる。
• se
  サンダーソンの電気陰性度。
• pe
  パウリの電気陰性度。一部希ガスなど、未定義の原子があるとエラーとなる。
• are
  オールレッド・ロコウの電気陰性度。一部希ガスなど、未定義の原子があるとエラーとなる。
• p
  分極率体積 (単位: $m^{-30} = Å^3$)。その原子の分極率に比例した値となる。
• i
  第一イオン化エネルギー (単位: eV) 。原子がイオンとして存在していても関係なく、常に「原子 (電荷0) → 1価の陽イオン + $e^-$」の変化に必要なエネルギーを指す。
• c
  (注: 「ATS」では使われない。後に登場する「ATSC」以降で使われる。)
  Gasteiger電荷。

AATS (#135 - #233)

ATSと同じく99個が存在する。
各ATS記述子について、その距離に該当する原子ペア数で割ったもの (平均をとったもの)。
該当するATSが計算できない場合、および該当する原子ペアがない場合はエラーとなる。

ATSC (#234 - #341)

(12原子パラメータ) × (9距離) の合計108個が存在する (ATSに比べ、原子パラメータに「c」が加わった)。
各原子パラメータをセンタリング (平均が0になるように変換) したのちに、先述のATSの式で計算したもの。

AATSC (#342 - #449)

ATSCと同じく108個が存在する。
各ATSC記述子について、その距離に該当する原子ペア数で割ったもの (平均をとったもの)。
該当するATSCが計算できない場合、および該当する原子ペアがない場合はエラーとなる。

MATS (#450 - #545)

(12原子パラメータ) × (8距離) の合計96個が存在する (ATSCに比べ、距離0が減った)。
AATSCの値を、各原子パラメータの分散で割ったもの。
該当するATSCが計算できない場合、該当する原子ペアがない場合、分散が0の場合はエラーとなる。
距離0の場合を計算すると、定義上必ず1となってしまうため、除いたものと思われる。

GATS (#546 - #641)

MATSと同じく108個が存在する。
(以下は作成中です)

E-state記述子 (#933 - #1248)

(以下は作成中です)