入試の「受験者平均点」「合格者平均点」「倍率」から「合格最低点」を求める

目的

中学・高校・大学等の入試の過去問を解く際、「受験者平均点」「合格者平均点」「倍率（合格者数 / 受験者数）」が公開されているが「合格最低点」が非公開の場合がある。
ここではその合格最低点を予測することを考える。

手法

以下のサイトで公開されているM中学の入試データ（2013～2019年度）を利用した。
ゴロゴロ中学受験
https://www.goro-goro.net/2019-musashi

各年度のデータについて、受験者平均点を $\mu_a$ 、合格者平均点を $\mu_p$ 、倍率を $r$ として、以下の操作を行った。
（各操作は次項で詳細に説明する。）

1. $\sigma$ の値を決める。受験者の得点が平均が $\mu_a$ 、標準偏差が $\sigma$ の正規分布に従うと仮定する。
2. 正規分布において、 $x > b$ の面積が $\frac{1}{r}$ となるような $b$ を暫定の合格最低点とする。
3. 分布の $x > b$ の部分の平均を求め、暫定の合格者平均点 ${\mu_p}^{\prime}$ とする。
4. ${\mu_p}^{\prime}$ と $\mu_p$ の大小関係から、標準偏差 $\sigma$ を更新し、1に戻る。これを繰り返す。
5. ${\mu_p}^{\prime}=\mu_p$ となったら、その時点での合格最低点 $b$ を予測値とする。

その後、合格最低点の予測値と実際の値をプロットし、簡単な予測（※）の場合と精度を比較した。
（※）合格最低点 = (受験者平均点 + 合格者平均点) / 2 であるという予測

手法の詳細

1. $\sigma$ の値を決める。受験者の得点が平均が $\mu_a$ 、標準偏差が $\sigma$ の正規分布に従うと仮定する。

受験人数が十分に多く、満点や零点の受験者がいない場合、この仮定は有効であると考えた。
もちろん、本当の得点分布は離散分布であるが、これを連続分布として考えている。

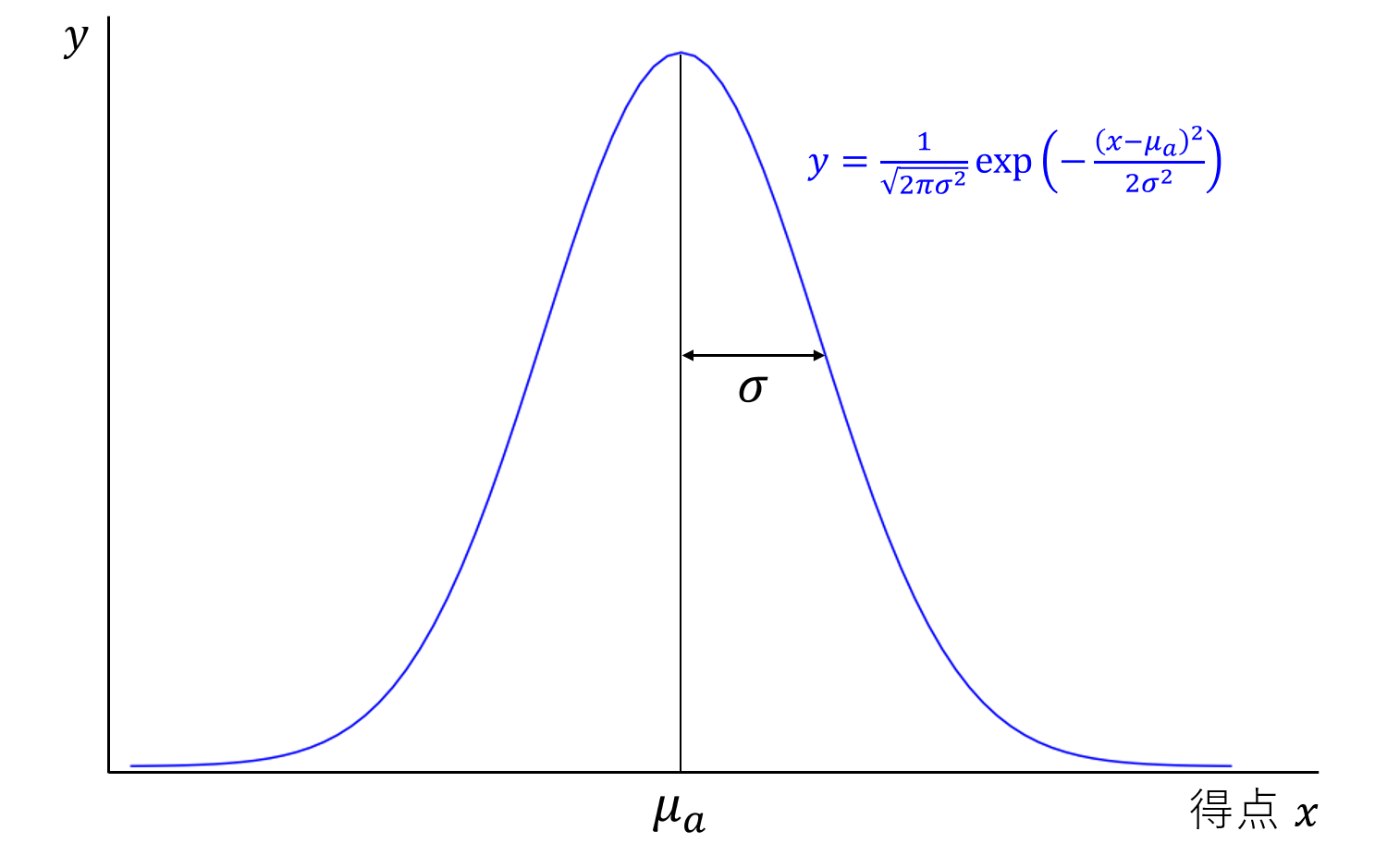
最初の $\sigma$ はてきとうに決めてよく、後々更新され最適値に近づいていく。
なお、上のグラフを「一人の受験生の得点の確率分布」と見るならば $y$ 軸は「確率密度（積分すると確率になる）」であり、「全受験生の得点分布」と見るならば $y$ 軸は「確率密度×人数（積分すると人数になる）」である。


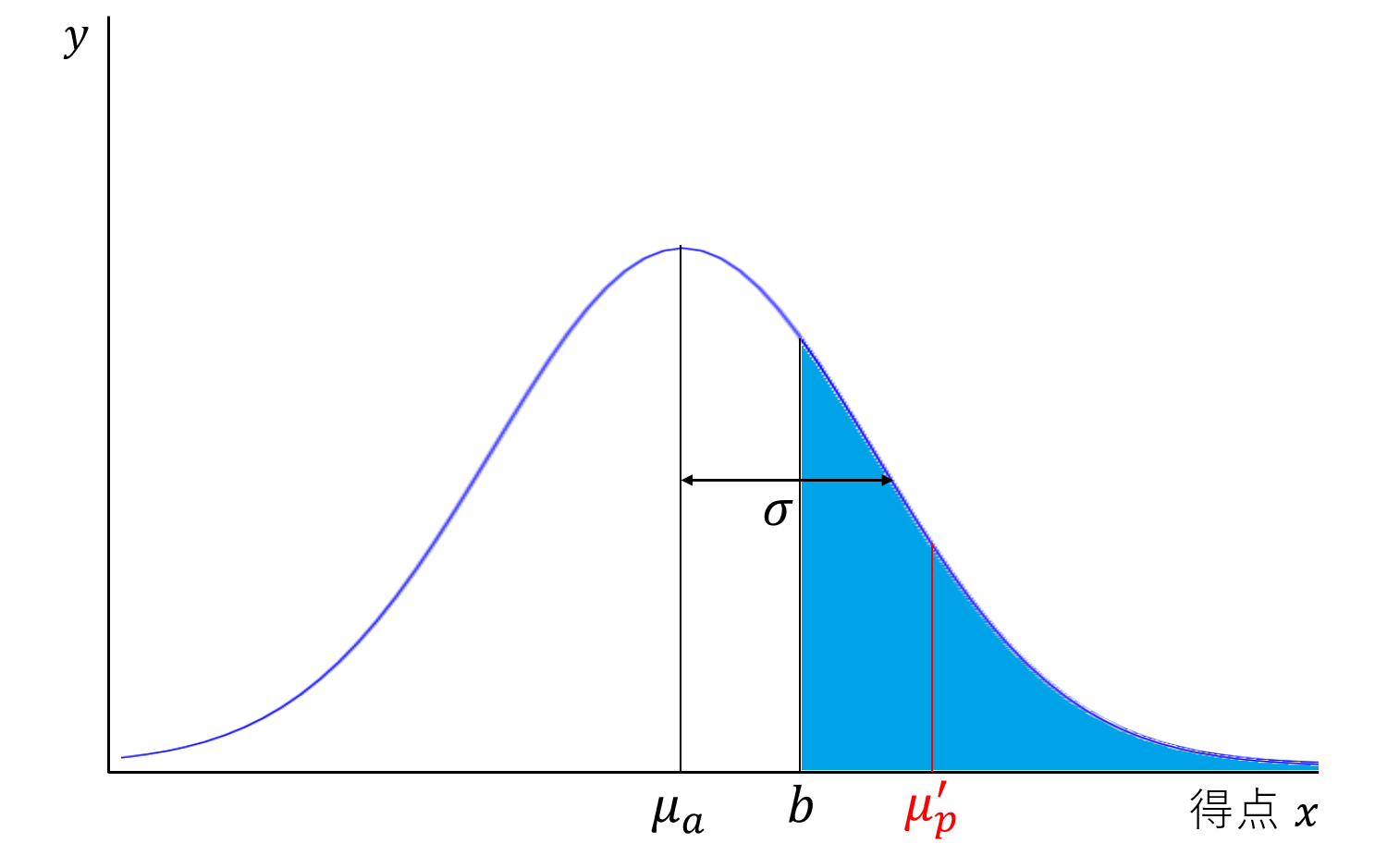
2. 正規分布において、 $x > b$ の面積が $\frac{1}{r}$ となるような $b$ を暫定の合格最低点とする。

これは数式で表すと

\int^{b}_{\infty} \frac{1}{\sqrt{2\pi{\sigma}^2}}\exp{\left(-\frac{(x-\mu_a)^2}{2\sigma^2}\right)} \mathrm{d}x = 1-\frac{1}{r}

を満たす $b$ を求めることに相当する。
左辺は、今回の正規分布の累積分布関数に $b$ を代入したものとなっている。
この式は解析的に解くことができないため、今回プログラミング（Python）を利用した（コードは後述）。

直線 $x=b$ が、得点分布で合格者と不合格者を分けているイメージである。


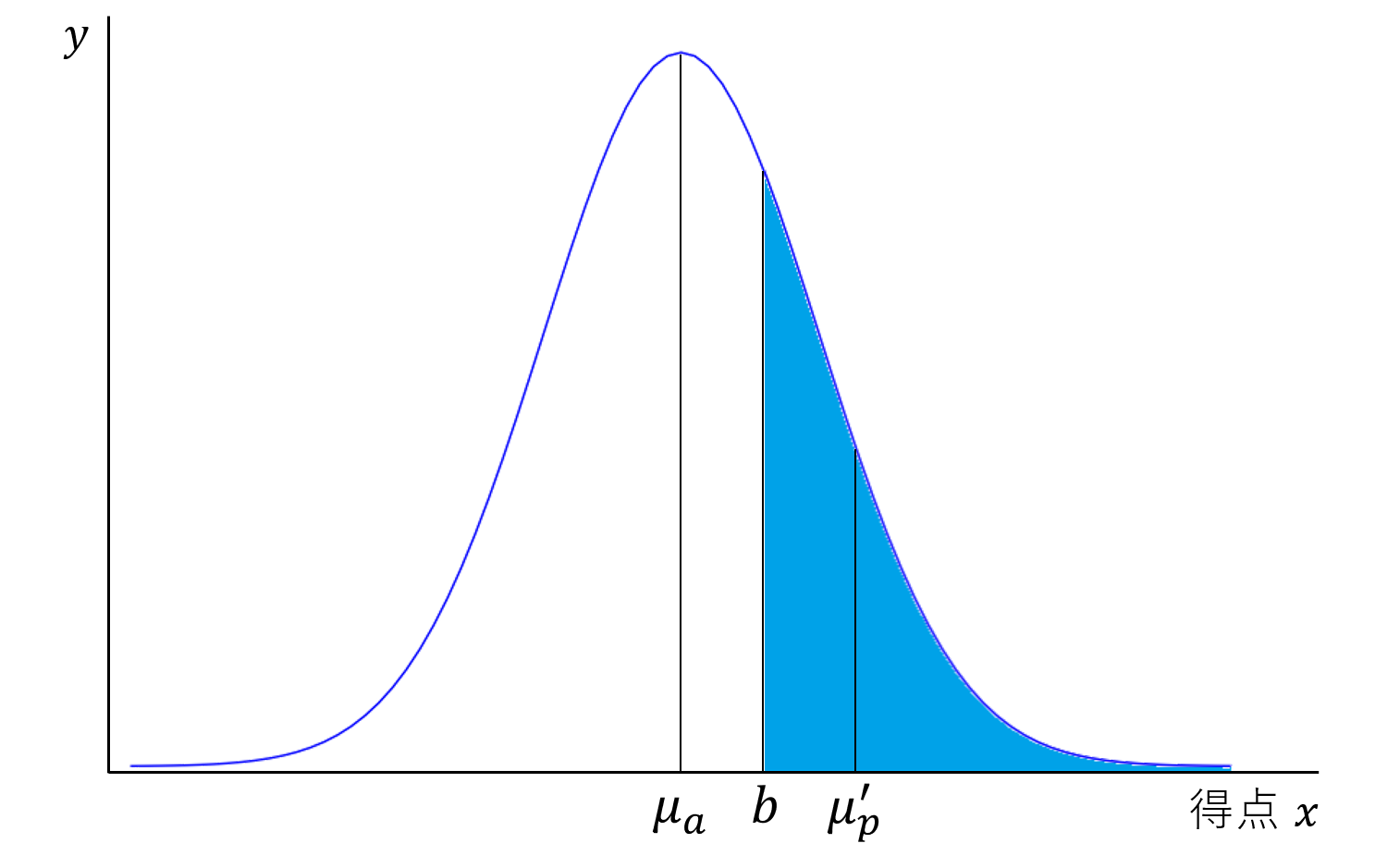
3. 分布の $x > b$ の部分の平均を求め、暫定の合格者平均点 ${\mu_p}^{\prime}$ とする。

これは、切断正規分布の平均（期待値）を求めることに相当し、

{\mu_p}^{\prime} = \mu_a + \sigma\frac{\phi\left(\frac{b - \mu_a}{\sigma}\right)}{1-\Phi\left(\frac{b - \mu_a}{\sigma}\right)}

と表される（ $\phi (\cdot)$ は標準正規分布の確率密度関数、 $\Phi (\cdot)$ はその累積分布関数を表す）。
参考：https://bellcurve.jp/statistics/blog/18075.html



4. ${\mu_p}^{\prime}$ と $\mu_p$ の大小関係から、標準偏差 $\sigma$ を更新し、1に戻る。これを繰り返す。

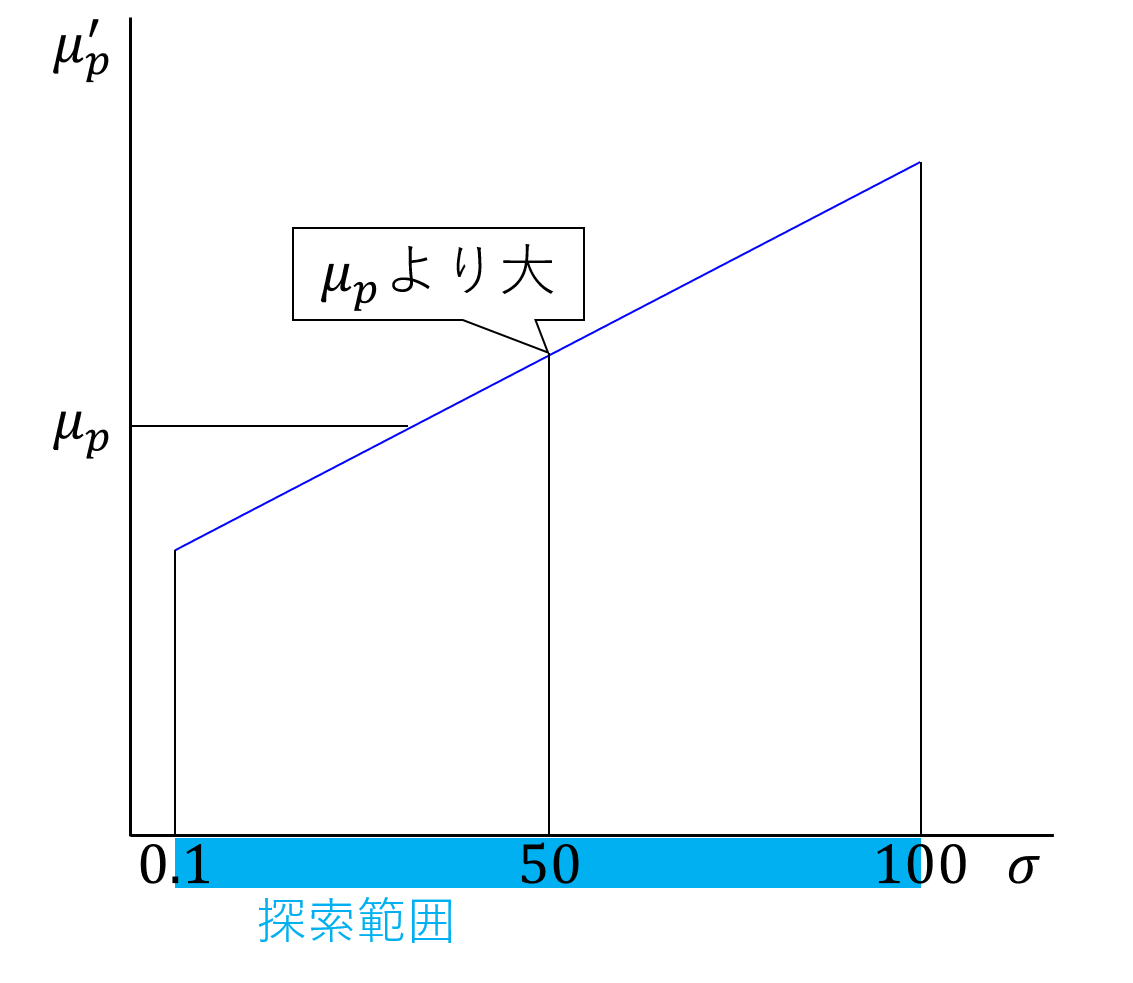
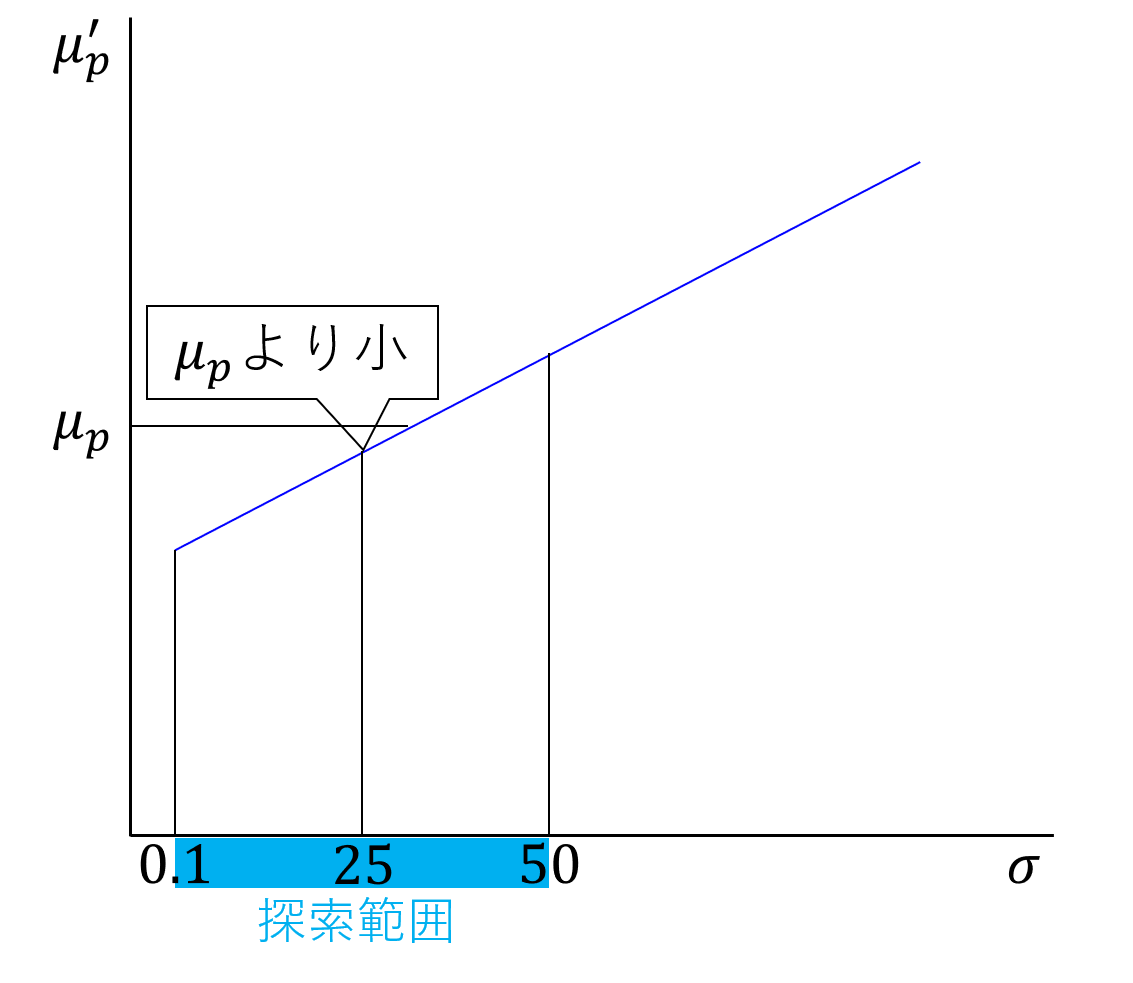
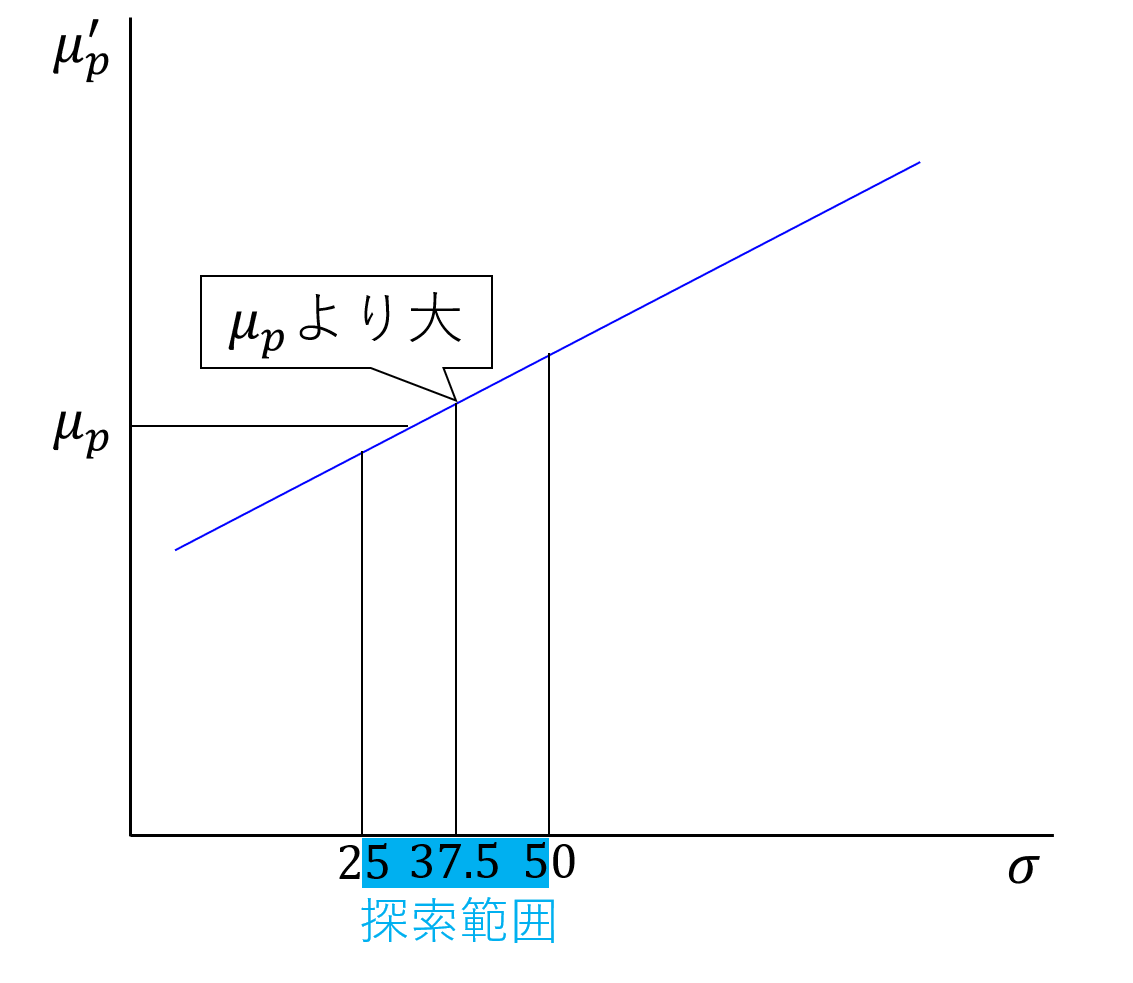上図のように、最初に決めた標準偏差 $\sigma$ が大きいほど ${\mu_p}^{\prime}$ は大きくなる（単調増加）ため、二分法を使い、${\mu_p}^{\prime} = \mu_p$ となる $\sigma$ を探索する。 上図のように毎回探索範囲が半分になるため、100回ほど繰り返すと十分な精度で目的の値にたどりつく。 （注）実は $\sigma$ と ${\mu_p}^{\prime}$ は上図の通り、1次関数の関係にある。そのため、実際には二分法を使わずに ${\mu_p}^{\prime} = \mu_p$ となる $\sigma$ を求めることができる。このことに解析後に気付いたが、計算精度や計算時間はほとんど変わらないため、二分法での解析をそのまま掲載した。
5. ${\mu_p}^{\prime}=\mu_p$ となったら、その時点での合格最低点 $b$ を予測値とする。

コードと結果

上記の「正規分布を使った予測」を行い、「合格最低点 = (受験者平均点 + 合格者平均点) / 2 であるという予測」と精度を比較した。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score, mean_absolute_error

# 2013-2019年度のデータ from https://www.goro-goro.net/2019-musashi
jukensya = [433, 556, 519, 590, 577, 541, 569]
goukakusya = [177, 177, 185, 183, 187, 185, 186]
juken_heikin = [138.5, 173.3, 172.9, 167.0, 165.5, 186.9, 170.5]
goukaku_heikin = [166.5, 210.7, 210.3, 202.0, 197.0, 221.5, 205.2]
goukaku_saitei = [146, 192, 188, 184, 180, 201, 185]

goukaku_saitei_pred = []

for i in range(7):  # 2013-2019年度の7回分を解析
    r = jukensya[i] / goukakusya[i]  # 倍率
    mu_a = juken_heikin[i]  # 受験者平均点
    mu_p = goukaku_heikin[i]  # 合格者平均点
    
    sigma_l = 0.1
    sigma_r = 1000
    sigma = (sigma_l + sigma_r) / 2  # 標準偏差を、0.1～1000の範囲で探索
    
    for i in range(100):  # 二分法を100回繰り返す
        b = norm.isf(1 / r, mu_a, sigma)  # 暫定の合格最低点
        mu_p_prime = mu_a + sigma * norm.pdf((b - mu_a) / sigma) \
                     / (1 - norm.cdf((b - mu_a) / sigma))  # 暫定の合格者平均点
        if mu_p_prime < mu_p:
            sigma_l = sigma
        else:
            sigma_r = sigma
        sigma = (sigma_l + sigma_r) / 2
    
    goukaku_saitei_pred.append(b)

# 受験者平均点と合格者平均点のちょうど中間点が合格最低点であるという予測
goukaku_saitei_pred_rough = [(goukaku_heikin[i] + juken_heikin[i]) / 2 for i in range(7)]

## R^2とMAEの確認 ##

print("Pred 1: 正規分布を使った予測の結果")
print("R^2: {:.4f}".format(r2_score(goukaku_saitei, goukaku_saitei_pred)))
print("MAE: {:.4f}".format(mean_absolute_error(goukaku_saitei, goukaku_saitei_pred)))
print("")
print("Pred 2: (受験者平均点 + 合格者平均点) / 2 であるという予測の結果")
print("R^2: {:.4f}".format(r2_score(goukaku_saitei, goukaku_saitei_pred_rough)))
print("MAE: {:.4f}".format(mean_absolute_error(goukaku_saitei, goukaku_saitei_pred_rough)))

## 実測値-予測値プロットの作成 ##

fig = plt.figure(figsize=(10, 5))
lim = [140, 220]  # 両軸の範囲
s = 17  # フォントサイズ

# Pred 1: 正規分布を使った予測の結果
ax0 = fig.add_subplot(1,2,1)

ax0.plot(goukaku_saitei, goukaku_saitei_pred, "o", markersize=8)
ax0.plot(lim, lim, "k-")

ax0.set_title('Pred 1', fontsize=s)
ax0.set_xlabel('True', fontsize=s)
ax0.set_ylabel('Predicted', fontsize=s)
ax0.tick_params(labelsize=s)
ax0.set_xlim(lim)
ax0.set_ylim(lim)
ax0.set_aspect('equal')

# Pred 2: (受験者平均点 + 合格者平均点) / 2 であるという予測の結果
ax1 = fig.add_subplot(1,2,2)

ax1.plot(goukaku_saitei, goukaku_saitei_pred_rough, "o", markersize=8)
ax1.plot(lim, lim, "k-")

ax1.set_title('Pred 2', fontsize=s)
ax1.set_xlabel('True', fontsize=s)
ax1.set_ylabel('Predicted', fontsize=s)
ax1.tick_params(labelsize=s)
ax1.set_xlim(lim)
ax1.set_ylim(lim)
ax1.set_aspect('equal')

# PNGとして保存
fig.tight_layout()
fig.savefig("plot.png")

出力
R^2値は決定係数であり、1に近いほど精度が良いことを意味する。
MAEは予測誤差の絶対値を平均したものであり、0に近いほど精度が良いことを意味する。

Pred 1: 正規分布を使った予測の結果
R^2: 0.9892
MAE: 1.4670

Pred 2: (受験者平均点 + 合格者平均点) / 2 であるという予測の結果
R^2: 0.9583
MAE: 2.5571

考察

正規分布を利用した予測であるPred 1は、簡単な予測であるPred 2より高精度であるといえる。
予測誤差の平均は約1.5点であり、実際の勉強の際の目安にも十分使えそうである。
また、Pred 2のプロットを見ると左下の145点付近のデータで予測誤差が大きくなっている。
これは、Pred 2では受験倍率に関係なく「受験者平均点と合格者平均点の中点の数値」を採用しているため、倍率の変化に対応できないことが原因と考えられる（この年だけ倍率が2.4倍と低い、他の年は2.8～3.2倍）。
一方、Pred 1では予測誤差が他データと同程度以下に抑えられており、正規分布を利用した手法は倍率の変化に対応できているといえる。

なお、Pred 1では多くのデータが「予測値が実際の値より1～2程度小さい」という似たようなずれ方をしている。
そのため、データが十分ある場合は、今回の「1～2程度」にあたる定数を求め、それを予測値に足す補正を加えることで、さらに良い精度となる可能性がある。

参考

scipy.stats - scipyの統計関数群のAPI - keisukeのブログ
http://kaisk.hatenadiary.com/entry/2015/02/17/192955

3-5. 歪度と尖度 | 統計学の時間 | 統計WEB
https://bellcurve.jp/statistics/course/17950.html

関連記事

札幌医科大学の受験者平均点を見積もる
https://qiita.com/hokudai_meiyo/items/cea6fce8633bbc46810e
こちらでは合格者の平均点や最低点から、受験者の平均点と標準偏差を予測している。