点過程と指数型Hawkes過程
はじめに
Hawkes過程の数学的な導入用の記事です.初回のテーマは以下の通りです.
- 1次元点過程とその強度過程を定義する.
- 1次元Hawkes過程を定義する.
- 1次元指数型Hawkes過程のお気持ちを理解する.
基礎的な測度論,確率論の知識を前提としますが,これらの知識がなくてもお気持ちは汲み取れるように書けたら嬉しいなと思っています.間違いを見つけたら指摘して欲しいです.もし,需要と僕のやる気があれば,
- 多次元Hawkes過程.
- マーク付きHawkes過程.
- Hawkes過程の統計学.
- Hawkes過程のPythonによるシミュレーション.
なども紹介できると面白いかなと思っています.
Hawkes過程とは
まず,点過程とはランダムに発生するイベントの発生時刻のモデルです.そして,Hawkes過程は過去のイベントに依存して未来の起きやすさが変動する点過程です.
例えば,あるツイートがどのような時間間隔でリツイート(RT)されるのかをモデリングしたいとしましょう.過去のRTは未来のRTを誘発する効果があります.しかし,その効果は時間と共に減衰していきます.Hawkes過程を用いるとこのような現象を記述することが出来ます.
歴史的には地震のモデル,株の板情報のモデル,感染症のモデル,脳のニューロンのモデルなどに使われてきましたが,近年ではその応用先は広がっています.
1次元点過程
$(\Omega, \mathscr{F}, (\mathscr{F}_t)_{t \ge 0}, P)$ をフィルトレーション付き確率空間とします.点過程とは以下のように増大する停止時刻の列を指します.
定義
**点過程(point process)**とは以下を満たす$\mathscr{F}_t$-停止時刻の列 $(T_n)_{n \in \mathbb{N}}$ である.
$$
0 < T_1 < \cdots < T_n < \cdots \quad a.s.
$$
$T_n$ は上の例だとn番目のRTが押された時刻に相当します.この記事では,$\lim_{n \to \infty} T_n = \infty ~~ a.s$ という制約を設けます.有限時間内に無限回イベントが起こることはないという意味です.この停止時刻から,計数過程とよばれる確率過程が作れます.
定義
以下で定まる確率過程 $N_t$ を**計数過程(counting process)**と呼ぶ.
$$
N_t = \sum_{n \ge 1} 1_{\{T_n \le t \}}.
$$
この確率過程 $(N_t, \mathscr{F}_t)$ を点過程と呼ぶことも多いです.計数過程は時刻 $t$ までに起きたイベントの数に対応しており,下図のように時刻 $T_n$ で1ずつ増加する階段状のパスを持ちます.

さて,この $(N_t, \mathscr{F}_t)$ は確率過程として以下のような性質を持つことがすぐに分かります.
- $N_t$ は $\mathscr{F}_t$-adapted である.
- $N_t$ のパスは単調非減少であり右連続かつ左極限を持つ.
- $N_{T_n} \le n \quad a.s.$
従って,$N_{t \wedge T_n}$ は一様可積分な$\mathscr{F}_t$-劣マルチンゲールとなり,Doob-Meyer分解から以下のような(indistinguishabilityの意味で)一意な分解を得ます.
$$
N_t = M_t + A_t.
$$
ここで, $M_t$ は$\mathscr{F}_t$-局所マルチンゲール,$A_t$ はpredictableかつ単調非減少なパスを持つ確率過程です.今度は逆に $A_t$ の構造を定める事で点過程 $T_n$ たちの分布を決定する事を考えましょう.特に,次のような強度過程を持つ点過程が重要視されます.
定義1
**強度過程(intensity process)**とは以下を満たす左連続かつ右極限を持つ確率過程 $\lambda_t$ である.
$$
A_t = \int_0^t \lambda_s ds.
$$
もし,$N_t$ が可積分であれば,マルチンゲール性と条件付き期待値に対するルベーグの収束定理から
$$
\lim_{h \to 0} \frac{E[N_{t+h}-N_t | \mathscr{F}_t]}{h} = \lim_{h \to 0} E\Bigg[\frac{1}{h}\int_t^{t+h} \lambda_s ds \Bigg| \mathscr{F}_t\Bigg] = \lambda_{t+}.
$$
を得ます.上式から, $\lambda_t$ は時刻 $t$ における $N_t$ の増加率の条件付き期待値を表します.$N_t$ の増加はイベントの発生を意味するため,$\lambda_t$ は時刻 $t$ におけるイベントの起きやすさを表す量であると言えます.強度過程の構造を指定して点過程の分布を決めた場合はそのような点過程が本当に存在するのかを確かめる必要がありますが,この記事では省略します2.
点過程の最も基本的な例としてはPoisson過程が挙げられます.これは,強度過程が常に一定の定数であるとした点過程です.
定義
強度過程が $\lambda_t = \lambda$,$(\lambda>0)$ である点過程をPoisson過程と呼ぶ.
Poisson過程はイベントがいつでも一定の確率で起きるモデルです.$N_t$ と $\lambda_t$ のシミュレーションの例は下図のような形です.($\lambda=5$)

Poisson過程はBrown運動のように独立定常増分を持つ点過程として定義する文献も多く見られます.
1次元Hawkes過程
Hawkes過程は上述の強度過程が自身の確率積分の形で表される点過程です.
定義
強度過程が
$$
\lambda_t = \phi\left( \int_0^{t-} h(t-s) dN_s \right)
$$
のように表せる点過程をHawkes過程と呼ぶ.ここで,$\phi \colon \mathbb{R} \to \mathbb{R}_+$,$h \colon \mathbb{R}_+ \to \mathbb{R}$ はボレル可測関数である.
ここで,$N_t$ は単調非減少であるため,$dN_t$ による確率積分はパス毎($\omega \in \Omega$ 毎)にリーマン=スティルチェス積分としても定めることが可能です.そして,$N_t$ はジャンプする大きさは1であり,ジャンプ時刻以外は一定であったため,実質は次のような総和として書き表すことができます.
$$
\lambda_t = \phi\left( \int_0^{t-} h(t-s) dN_s \right) = \phi\left( \sum_{T_n < t} h(t-T_n) \right).
$$
この,確率積分のタームによって強度過程に時刻 $t$ より前に起きた過去のイベント達の影響を組み込むことができます.$\phi$ としては $\phi(x) = \mu + x$,($\mu>0$) のような線形な関数を想定することが多いです.$h$ はカーネル関数と呼ばれ,過去のイベントがどのようなダイナミクスで $\lambda_t$ に影響するのかを表現します.$h$ は自由に定めることが可能ですが3,$\phi$ が上述の形の場合は以下の定常性の条件を満たす必要があります4.
$$
\int_0^{\infty} \lvert h(s) \rvert ds < 1.
$$
ここでの定常性とは,直感的には $\lim_{n \to \infty} T_n = \infty ~~ a.s.$ が保たれる事を指します.すなわち,$h(t)$ が $t$ が大きくなるにつれて十分に減衰しないと $\lambda_t$ が発散してしまい,有限時間内に無限回イベントが発生し得るモデルとなってしまう事を意味しています.次の指数型Hawkes過程を考えるとより具体的なイメージが湧くと思います.
指数型Hawkes過程
指数型Hawkes過程はその性質の良さから最も頻繁に用いられるHawkes過程です.
定義
強度過程が
$$
\lambda_t = \mu + \int_0^{t-} \alpha e^{-\beta (t-s)} dN_s
$$
のように表せる点過程を**指数型Hawkes過程(exponential Hawkes process)**と呼ぶ.ここで,$\mu$,$\alpha$,$\beta$ は正の定数で $\alpha/\beta<1$ を満たす.
直ぐに分かるように,これは $\phi(x) = \mu + x$,$h(s) = \alpha e^{-\beta s}$ としたHawkes過程で,パラメータの条件は
$$
\int_0^{\infty} \lvert h(s) \rvert ds = \int_0^{\infty} \alpha e^{-\beta s} ds = \frac{\alpha}{\beta} < 1
$$
からきています.指数型Hawkes過程の$N_t$ と $\lambda_t$ のシミュレーションの例は下図のような形です.($\mu=1$,$\alpha=0.5$,$\beta=0.8$)
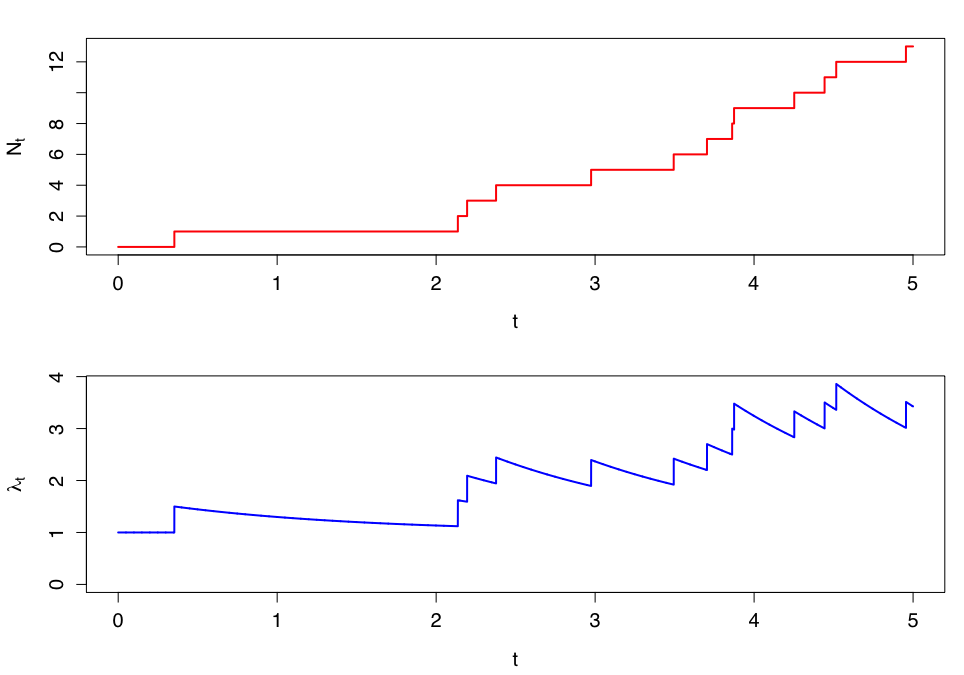
下図の強度過程のグラフに注目してください.まず,ベースとして $\mu=1$ だけ $\lambda_t$ の値が持ち上がっています.このパラメータ $\mu$ は前述のPiosson過程と同等の働きをするパラメータで「いつでも $\mu=1$ だけはイベントが起きやすい状態」を記述しています.次に一度イベントがあると $\alpha=0.5$ だけ $\lambda_t$ の値がジャンプしています.これは,最初のTwitterの例ではRTによって強度過程の値に換算して $0.5$ だけそれ以降のRTが発生しやすくなったと言う事を意味します.しかし,その影響は $e^{-\beta t} = e^{-0.8t}$ の速さで時間 $t$ と共に減衰していきます.このようなダイナミクスによって,
「イベントが連続して起きるほど強度過程は大きな値となる」$\leftrightarrow$「強度過程の値が大きくなるとイベントが起きやすくなる」
という相互作用を経て,トレンドを形成するようなモデルを表現できます.また,確率微分方程式(SDE)を扱ったことがあれば,強度過程が以下の形で表される事からもイメージを掴みやすいです.
$$
d\lambda_t = \beta(\mu - \lambda_t)dt + \alpha dN_t, \quad \lambda_0 = \mu.
$$
$\lambda_t$ の変動は第1項の指数減衰と第2項のジャンプで説明される事が見て取れます.このSDEの解が指数型Hawkes過程の強度過程となることは,伊藤の補題から導くことができます.
おまけ
指数型Hawkes過程が数学者の間で人気である理由の一つとして,強度過程がMarkov性を有するという事が挙げられます.この証明は難解ですが,直感的には以下のような変形が可能であることに由来します.
\begin{align}
\lambda_t
&= \mu + \int_0^{u-} \alpha e^{-\beta (t-s)} dN_s + \int_u^{t-} \alpha e^{-\beta (t-s)} dN_s \\
&= \mu + \int_0^{u-} \alpha e^{-\beta (t-u)} e^{-\beta (u-s)} dN_s + \int_u^{t-} \alpha e^{-\beta (t-s)} dN_s \\
&= \mu + e^{-\beta (t-u)}(\lambda_u - \mu) + \int_u^{t-} \alpha e^{-\beta (t-s)} dN_s
\end{align}
ここで,最後の式より $\lambda_t$ の値は $\lambda_u$ の値と時刻 $u$ 以降のジャンプにより決定すると分かります.すなわち,時刻 $u$ 以前のジャンプの履歴は $\lambda_u$ に集約されていると考えられます.Markov過程に対しては様々な研究がなされており,それらの知見を活かしてエルゴード性などの性質を指数型Hawkes過程に対して証明する事ができます.そして,これらの漸近的性質の応用として,指数型Hawkes過程に関連する統計学の理論が展開されています.