2分ヒープ
2分ヒープは2分木を利用したデータ構造の一つで、プライオリティキューを効率的に実現する。
2分ヒープでは2分木をポインタで表現するのではなく、2分木のノードに番号を付けて配列でもつように実装されることがよくある。
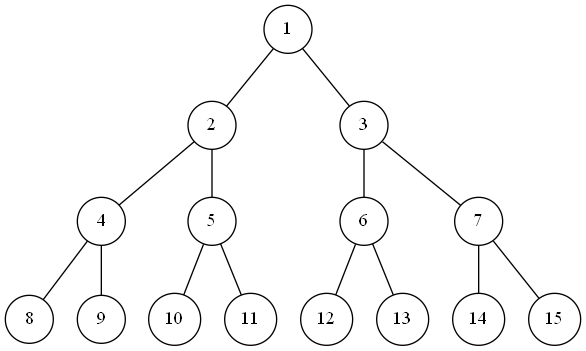
配列での実装する際のノードの番号付け
2分木の各ノードに対して、図のように番号を振る。
この時、自身のノードに対して子番号と親番号は以下のようになるが、これの説明。
- 左の子: $2n$ 右の子: $2n + 1$
- 親 : $floor(\frac{n}{2})$
[1.の説明]
2分木の深さ$d$におけるノード数は$2^d (d=0, 1, 2,...)$であり、深さ$d$以下の全ノード数は
2^0 + 2^1 + … + 2^d = \frac{(1 - 2^(d+1))}{(1-2)} = 2^(d+1) - 1
となる。そのため、各深さ$d$における一番左のノードのindexは$(2^d-1)+1 = 2^d$であり、
この一番左のノード$2^d$に対する、左の子は$2^(d+1)=2*2^d$、右の子は$2*2^d + 1$で1.が成り立つ。
深さ$d$の左から$i-1$番目のノード$n-1$に対して1.が成立すると仮定する。
深さ$d$の左から$i$番目のノード$n$に対する左の子の番号は、左から$i-1$番目のノードの右の子の次なので
$(2(n-1) + 1) + 1 = 2n$となって1.がノード$n$に対しても成立する。
よって帰納的に任意の深さ$d$の全ノードに対して1.が成立する。
[2.の説明]
深さdの一番左のノードに対しては、ノード番号が$2^d$で親は$2^(d-1)$なので2.が成り立つ。
また、その次のノードの親は同じ親で、$floor(\frac{2^d + 1}{2}) = floor(2^(d-1) + 0.5)=2^(d-1)$なので2.が成り立つ。
深さ$d$の左から$2i-1$番目のノードに対して2.が成り立つと仮定する。
左から$2i+1$番目のノード$n$に対する親番号は左から$2i-1$番目の親の次であるので、
$floor(\frac{n-2}{2}) + 1 = floor(\frac{n-2}{2} + 1) = floor(\frac{n}{2})$
となって2.が成り立つ。
同様に左から$2i$番目のノードに対して2.が成り立つと仮定すると、左から$2i+2$番目のノード$n$に対しても2.が成り立つ。
よって帰納的に任意の深さ$d$の全ノードに対して2.が成立する。
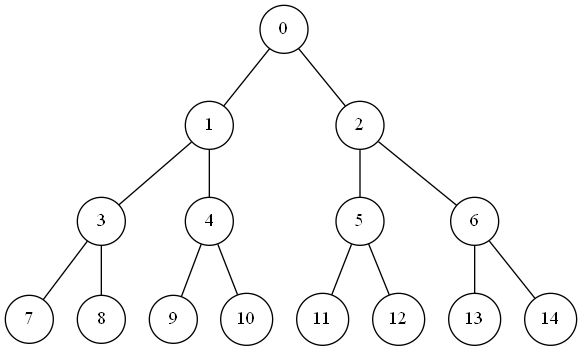
0始まりのノード番号を付ける場合
以下のように0始まりの番号を付ける。
1始まりのノード番号をn、0始まりのノード番号を$n'$とすると、$n' = n - 1$
あるノードに対する左の子は1始まりの番号では、$2n = 2(n'+1)$で、これを0始まりに直して$2(n' +1) -1 = 2n' + 1$、右の子は$2n'+2$となる。
親についても1始まりの番号では、$floor(\frac{n}{2})=floor(\frac{n'+1}{2})$で、これを0始まりに直して$floor(\frac{n'+1}{2}) - 1 = floor(\frac{n'+1}{2} - 1) = floor(\frac{n'-1}{2})$
終わりに
プログラミングコンテストチャレンジブックを読んで、どうしてこうなるのか小一時間考え込んでしまったのでメモ